量子人工智能引论：一阶量子逻辑语义

很多重要的逻辑，包括量子逻辑中元逻辑的独特性已在语句层次出现【53】。同时，将语句层次的量子逻辑扩充到一阶逻辑已成为很自然的事情【54】。因此，首先介绍量子逻辑。作为语句的量子逻辑情形，我们将刻画的一阶量子逻辑是代数的，又是克里普克（Kripkean）语义的。

假定有一个标准的一阶语言，其谓词为，个体常元为am。为简单起见，此处没有假设函数符号以及基本的逻辑联结词，如：¬（否定）、∧（析取）、∨（合取）和∀（全称量词），以及项、公式和语句（语句是没有自由变元出现的公式）等概念，用通常方法进行定义。将使用x，y，z，…xn等作为个体变元的元变量，使用t，t1，t2，…作为所有项的元变量。存在量词用德.摩根定律来定义：

定义5.1 一阶量子逻辑的代数化

一阶量子逻辑的代数化是一个系统：A＝（BC,D,ν)

其中：

（1）对于任意F∈C（C 是B 的子集的特定族），在下确界∧和上确界∨条件下，BC＝(B,≤,′,0,1)是一闭的正交格。

（2）D 是非空集合（与B 不相交），叫做A 的域。

（3）v 是满足下列条件的赋值函数：

②对于域D 中的变量的任意解释σ（即对于所有变量集映射到D 的任意函数），一个对（ν,σ）（缩写为νσ，并称为广义赋值），根据下列条件，指派任意项为D 的一个元素和任意公式为B 的一个元素：

σ[x/d]是指派x 给个体d 的一个解释，而指派给x 的很多值是与σ 不同的。

定义5.2 真值与逻辑真值

公式α 在A＝（BC,D,ν）中为真（缩写为⊧Aα），当且仅当，对于变量σ 的任意解释，有νσ（a）=1；a 是量子逻辑（缩写为⊧QLα）的逻辑真值，当且仅当，对于任意的A，有⊧Aα。

定义5.3 实现结果和逻辑结果

定义5.4 （一阶）量子逻辑的克里普克实现。

（一阶）量子逻辑的克里普克实现是一个系统：

其中：

（1）（I,R,PrC）满足句子情形中的相同条件；对于任意F⊆PrC，使得F∈C（这里C 是PrC 的子集的特定族）的交∩，PrC 是闭的。

（2）U（称为K 的域）是世界I 的集合的交的一个非空集合。U 的元素是个体概念u，使得对于任意世界i，u（i）是一个个体（叫做世界i 中u 的引用）。一个个体概念u 是稳定的，当且仅当，对于任意世界对i、j，u（i）＝u（j）。集合Ui={u（i）：u∈U}表示世界i 中的个体域。对于任意i、j，总有Ui=Uj，称之为K 的实现有一个稳定的域。

（3）根据下列条件，V 与任意个体常元am 和任意谓词Pn m 的一个意义相关联：

V（am）是U 中的一个个体概念；

定义5.5 可满足性

定义5.6 可核验性

定义5.7 真值和逻辑真值

定义5.8 实现结果和逻辑结果

以类似的方式，通过要求任何实现都是正交模的，可以获得一阶量子逻辑的代数和克里普克特征。

关于一阶量子逻辑的语义，可以证明下列一致的引理。

引理5.1

给定A=（BC,D,ν）和K＝（I,R,PrC,U,V）：

（1）如果σ 和σ*的属性值与项t 的变量一致，则

（2）如果σ 和σ*的属性值与项t 的非约束变量一致，则(www.xing528.com)

如同句子的情形，我们容易证明下面的引理。

引理5.2

（1）对于任意代数实现A，存在一个克里普克实现KA，使得对于任意α，当且仅当⊧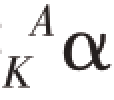，有⊧Aα。进而，如果A 是正交模，则KA也是正交模【55】。

（2）对于任意克里普克实现K，存在一个代数实现AK，使得对于任意α，当且仅当⊧AKα，有⊧Kα。进而，如果K 是正交模，则AK也是正交模。

一阶量子逻辑（OQL）的公理化可以通过添加量子逻辑语句计算规则而得到下列新规则：

其中，α（x/t）表示合法置换；

其中，x 是T 中的约束变元。

所有基本的句法记号可被定义成语句情形。一致的语句集合T 有一致的归纳扩展T*，使得T*├∀xα（x），无论如何，对于任意常项t，有T*├α(t)。弱Lindenbaum 定理可以被加强，如下：

如果T├¬α，则存在一致的归纳T*，使得T 语法上与T*一致，且T*├α。

其中，T 语法上是与T*一致的，当且仅当，不存在公式α，使得T├α 且T*├¬α。

我们可以根据克里普克语义证明对于这个演算的合理性和完全性定理。

定理5.1 合理性

证明：根据定义5.5 和定义5.8，可直接证明。

定理5.2 完全性

证明：作为语句情形，构造一个规范的模型K＝（I,R,PrC,U，V），使得T├α，当且仅当T ⊧Kα。它是满足的。

定义5.9 一阶量子逻辑规范模型的定义

（1）I 是所有一致的、闭的演绎集合和用普通语言LK（它是元语言的扩展）表示的句子的归纳集合；

（2）作为句子的情形，R 是确定的：

（3）U 是一个刚性的个体概念的集合，它是由扩充语言LK 的所有个体常元的集合自然确定的。对LK 的任意常元c，令uc 是与U 中的个体常元c相对应的个体概念。我们要求，对于任意世界i，uc（i）=c。换言之，在任何世界中，个体概念uc 的引证是常元c。用cu 表示对应于u 的常元。

（4）V（am）=uαm

这个V 是熟知的。可以证明，对于LK 中的任意句子α：

（5）PrC 是公式所有意义的集合，即X∈PrC，当且仅当∃α∃σ（X=Vσ（α））；C 是对于任何公式β 的所有集合{Vσ[x/u]（β）：u∈U}的集合。容易核检，K 是常元域的一个实现。引理5.3 规范模型引理

对于任意的α 和任意i∈I，以及任意σ，有：

其中，ασ 是通过与个体概念σ（x）相对应的常元cσ（x）代换α 中任意自由变元x 而得到的句子。

一阶量子逻辑容易用恒等式（通过标准方法）扩充到一阶逻辑。但一个关键问题是用开发的可能性表示，在这个逻辑里，就是用满足性理论描述。主要困难性可略证如下：一个自然条件是要求用ι 算子的任意特征，若∃x{β（x）⋏∀y[（β（y）⋏x=y）⋎x=y）⋎（¬β（y）⋏¬x=y）]⋏α(x)}为真，则α（ιxβ（x））为真。

但是，在量子逻辑中，这个蕴涵的前件的真值一般并没有保证存在特定个体，使得ιxβ（ι 是一个算子）能够处理成这样的个体的名字。作为一个反例，让我们考虑下面的情形（用代数语义）。令A=（B,D,υ），其中B 是基于平面R2所有闭子空间的集合的完全的正交模格，D 只含有元素d1和d2。令P 是一元谓词，X 和Y 是使得υ（P）（d1）=X，υ（P）（d2）=Y 的B 的两个正交的一维子空间。如果等式谓词“=”被解释成标准恒等关系（换言之，如果νσ（t1）=νσ（t2），则νσ（t1=t2）=1，否则νσ（t1=t2）=0），容易计算υ（∃x[Px⋏∀y(（Py⋏x=y）∨（¬Py⋏¬x=y））]）=1。

但是，对于域D 的两个元素d1和d2，我们有：

换言之，域中没有精确个体满足谓词P 表示的性质。