老吕数学要点精编（第8版）基础篇：排列组合方法简介

1.加法原理与乘法原理

1.1　加法原理

如果完成一件事有n类办法,只要选择其中一类办法中的任何一种方法,就可以完成这件事,若第一类办法中有m1种不同的方法,第二类办法中有m2种不同的方法,……,第n类办法中有mn种不同的方法,那么完成这件事共有N=m1+m2+…+mn种不同的方法.

1.2　乘法原理

如果完成一件事,必须依次连续地完成n个步骤,这件事才能完成,若完成第一个步骤有m1种不同的方法,完成第二个步骤有m2种不同的方法,……,完成第n个步骤有mn种不同的方法,那么完成这件事共有N=m1·m2·…·mn种不同的方法.

典型例题

例5某人要选择一辆交通工具由济南出发去北京,已知他有5辆汽车、3辆摩托车、4辆三蹦子,则他选择交通工具的方法有(　　)种.

(A)8　　　　(B)60　　　　(C)19　　　　(D)12　　　　(E)以上选项均不正确

【解析】加法原理.他从济南到北京一共有三类办法,即从汽车、摩托车、三蹦子其中一类中任选一辆,就可以完成这件事.由加法原理可得,一共有5+3+4=12(种)方法.

【答案】(D)

例6有5人报名参加3项不同的培训,每人都只报一项,则不同的报法有(　　).

(A)243种(B)125种(C)81种

(D)60种(E)以上选项均不正确

【解析】乘法原理.每个人都有3种选择,所以不同的报法有35=243(种).

【答案】(A)

例7 3个人争夺4项比赛的冠军,没有并列冠军,则不同的夺冠可能有(　　)种.

(A)43(B)34(C)4×3

(D)2×3(E)以上选项均不正确

【解析】每个冠军都有3个人可选,故不同的夺冠可能有34种.

【易错点】如果人去选冠军,可能会有2个人都想当某个项目的冠军,与题干没有并列冠军相矛盾,故必须是冠军去选人.

【答案】(B)

住店问题:

n个不同的人(不能重复使用元素),住进m个店(可以重复使用元素),那么第1个,第2个,……,第n个人都有m种选择,则总共有mn种不同的住店方法.

例8从5名男医生、4名女医生中选2名医生组成一个医疗小分队,要求其中男、女医生都有,则不同的组队方案共有(　　)种.

(A)20(B)30(C)40(D)10(E)60

【解析】第1步:从5名男医生中任选1名,共5种方法.

第2步:从4名女医生中任选1名,共4种方法.

根据乘法原理,共有5×4=20(种).故不同的组队方案共有20种.

【答案】(A)

例9某公司员工义务献血,在体检合格的人中,O型血的有10人,A型血的有5人,B型血的有8人,AB型血的有3人.若从四种血型的人中各选1人去献血,则不同的选法共有(　　)种.

(A)1200(B)600(C)400(D)300(E)26

【解析】由乘法原理可得,不同的选法共有10×5×8×3=1200(种).

【答案】(A)

2.排列数与组合数

2.1　排列数

(1)排列

从n个不同元素中,任意取出m(m≤n)个元素,按照一定顺序排成一列,称为从n个不同元素中取出m个元素的一个排列.

(2)排列数

从n个不同元素中取出m个元素(m≤n)的所有排列的种数,称为从n个不同元素中取出m个不同元素的排列数,记作.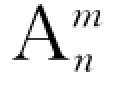

当m=n时,即从n个不同元素中取出n个元素的排列,称为n个元素的全排列,也称n的阶乘,用符号n!表示.

(3)排列数公式

典型例题

例10此公路上各站之间共有90种不同的车票.

(1)一条公路上有10个车站,每两站之间都有往返车票.

(2)一条公路上有9个车站,每两站之间都有往返车票.

【解析】每两站之间有往返票,则产生了顺序的区别,用排列数.

【答案】(A)

例11计划在某画廊展示10幅不同的画,其中1幅水彩画、4幅油画、5幅国画,排列一行陈列,要求同一品种的画必须放在一起,并且水彩画不放在两端,那么不同的陈列方式有(　　)种.

【答案】(D)

2.2　组合数(www.xing528.com)

(1)组合

从n个不同元素中任取m(m≤n)个元素组成一组(不考虑元素的顺序),称为从n个不同元素中任取m个元素的一个组合.

(2)组合数

典型例题

【答案】(B)

例13此公路上各站之间共有90种不同的车票.

(1)一条公路上有10个车站,每两站之间都有单程车票.

(2)一条公路上有9个车站,每两站之间都有单程车票.

【解析】每两站之间有单程票,只保证任选2站有票即可,不需要讨论站点的顺序,用组合数.若每两站之间有了往返票,则产生了顺序的区别,要用排列数.

【答案】(E)

例14某次乒乓球单打比赛中,先将8名选手等分为2组,进行小组单循环赛.若一位选手只打了1场比赛后因伤退赛,则小组赛的实际比赛场数是(　　)场.

(A)24(B)19(C)12(D)11(E)10

【解析】单循环赛,用组合数.

每两人之间比赛一场,每组4人,计划每组进行的比赛数为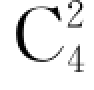=6(场);

每人在小组赛内与另外三人各比赛一场,计划每人比赛数为3场;

因伤退赛的选手只打了1场,故少赛了2场.

所以总比赛场数为2×6-2=10(场).

【答案】(E)

例15有1元、2元、5元、10元、50元的人民币各一张,取其中的一张或几张,能组成(　　)种不同的币值.

(A)20(B)30(C)31(D)36(E)41

【答案】(C)

例16某幢楼从二楼到三楼的楼梯共11级台阶,上楼可以一步上一级,也可以一步上两级,则不同的上楼方法共有(　　)种.

(A)34(B)55(C)89(D)130(E)144

【解析】设走m个一级,n个二级,则必须有m+2n=11,故需分为以下几类:

【答案】(E)

3.二项式定理

典型例题

【答案】(D)

【答案】(B)

本节习题自测

1.办公室有6个员工,现每天晚上需要3个员工值班,要求每两天值班的人不能完全一样,那么这6个人可以有(　　)种不同的值班情况.

(A)10(B)15(C)20(D)48(E)120

2.甲组有5名男同学、3名女同学;乙组有6名男同学、2名女同学.若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有(　　)种.

(A)150(B)180(C)300(D)345(E)420

3.有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人承担.现从10人中选派4人承担这三项任务,不同的选派方法有(　　).

(A)1260种(B)2025种(C)2520种

(D)5040种(E)5080种

4.由0,1,2,3组成无重复数字的4位数,其中0不在十位的4位数有(　　)个.

5.共有432种不同的排法.

(1)6个人排成两排,每排3人,其中甲、乙两人不在同一排.

(2)6个人排成一排,其中甲不站排头.

习题详解

1.(C)

【解析】6个员工选3个,可以有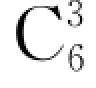=20(种)不同的值班情况.

【注意】用C做运算时,不可能有两次完全一样的结果.

2.(D)

【解析】恰有1名女同学,那么这个女同学可能来自甲组,也可能来自乙组,则不同的选法共有

3.(C)