计算机组成原理中的浮点加法器：流水线设计及结构图

浮点加法器一般采用流水线设计技术。

1.流水线原理

计算机的流水处理过程同工厂中的流水装配线类似。为了实现流水，首先必须把要处理的任务分割为一系列子任务，使各子任务能在流水线的各个阶段并发地执行，将任务连续不断地输入流水线，从而实现了子任务级的并行处理。流水处理大幅度地改善了计算机的系统性能，是在计算机上实现时间并行性的一种非常经济的方法。

在流水线中，原则上要求各个阶段的处理时间都相同。若某阶段的处理时间较长，势必造成其他阶段的空转等待。因此对子任务的划分是决定流水线性能的一个关键因素。

假若任务T被分成k个子任务，可表示成T=｛T1，T2，…，Tk｝，各个子任务之间有一定的先后关系：若i＜j，则必须在Ti完成以后，Tj才能开始工作。具有这种线性先后关系的流水线称为线性流水线。线性流水线的硬件基本结构如图2-6所示。

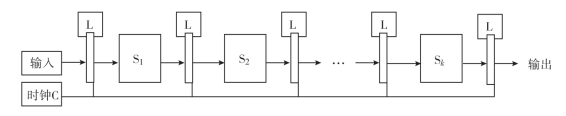
图2-6　线性流水线的硬件基本结构

图2-6中，处理一个子任务的过程称为过程段（Si）。线性流水线由一系列串联的过程段组成，各个过程段之间设有高速的缓冲寄存器（L），以暂时保存上一过程段子任务处理的结果。在一个统一的时钟（C）控制下，数据从一个过程段流向相邻的过程段。

设过程段Si所需的时间都相等为t，缓冲寄存器的延时也相等为τ，则线性流水线的时钟周期定义为t+τ。在流水线处理中，当任务饱满时，任务源源不断地输入流水线，不论有多少级过程段，每隔一个时钟周期都能输出一个任务。从理论上说，一个具有k级过程段的流水线处理n个任务需要的时钟周期数为Tk=k+（n-1），其中k个时钟周期用于处理第一个任务。k个周期后，流水线被装满，剩下的n-1个任务只需要n-1个周期就完成了。如果用非流水线的硬件来处理这n个任务，时间上只能串行进行，则所需时钟周期数为TL=n×k。我们将TL和Tk的比值定义为k级线性流水线的加速比，理论上k级线性流水线处理几乎可以提高点倍的速度。但实际上由于存储器冲突、数据相关等问题，这个理想的加速比不一定能达到。

2.流水线浮点加法器(www.xing528.com)

流水线浮点加法器一般由4级线性流水线构成。假若有两个规格化的浮点数A=a×2p和B=b×2q，其中a和b为已规格化的二进制纯小数。现用流水方法求浮点加法

C=A+B=c×2r=d×2s

其中，r=max（p，q），d是规格化的尾数。4级流水线浮点加法器分为以下4个过程段。

①求阶差。比较p和q，求r=max（p，q），t=｜p-q｜。

②对阶。将阶数较小的尾数右移t位，使两个加数的阶数相同。

③相加。两个尾数相加，得到和数C（为简单，设0＜C≤1）。

④规格化。计算C的小数点后第一个“1”以前的“0”的个数u，然后将C左移u位，得到规格化小数d=c×2u及指数s=r-u。

流水线浮点加法器的结构图略。