逐差法是常用的数据处理方法之一,常常用它来求一般线性方程中的待定系数。若实验中,自变量x作等差变化(等间距变化),测量数据的对应关系为

一般只测两组数据,由两个方程相减求差就可求出b,进而求出a。但是,为了减少误差,现在测了n+1组,怎样求差才能充分利用数据?下面先采用每两个相邻的方程相减求差的方法。由每两个相邻的方程相减求差后,有
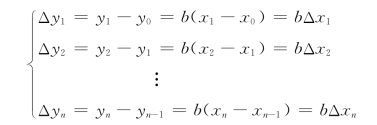
将等式两边取平均,可得
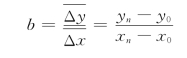
这是因为
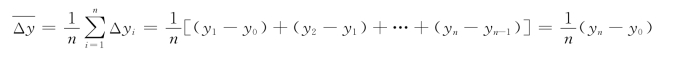
同理
![]()
这样一来,只有首、末两组数据起作用,而中间的数据都一一抵消了。上述相减求差的方法是不可取的,它没有充分利用数据。下面介绍一种特殊的求差方法。
将多次测量的数据分成数目相同的前、后两组,然后将前、后两组的相应项依次相减求差,这种方法称作逐差法(环差法)。为讨论方便,设测量数据共有2n组,每组n个方程,即
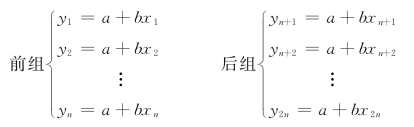
将前、后两组的对应项相减求差,得
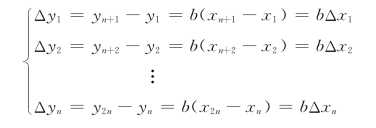
等式两边取平均,得(https://www.xing528.com)
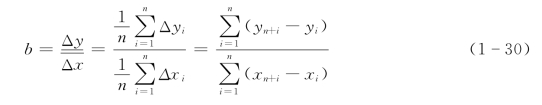
为求a,再由
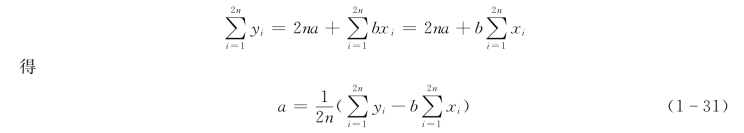
应该指出,上述求a、b的方法,为一次逐差法。当求一元二次方程的系数时,还应对测量数据连续分两次计算,即采用二次逐差法,在此不再赘述,可查阅有关文献。
总之,一次逐差法充分利用测量数据,具有对数据取平均的效果,比作图法精确,减少了误差,在物理实验中常被采用。但是,用逐差法处理的问题只限于多项式形式的函数关系,而且自变量需等间距变化,这是该方法的局限性。
例1-14 用拉伸法测定弹簧的劲度系数。已知在弹性限度范围内,伸长量x与拉力F之间满足如下关系:
F=kx
等间距地改变拉力(负荷),将测得一组数据,如表1-4所示。
表1-4 伸长量x与拉力F相关数据
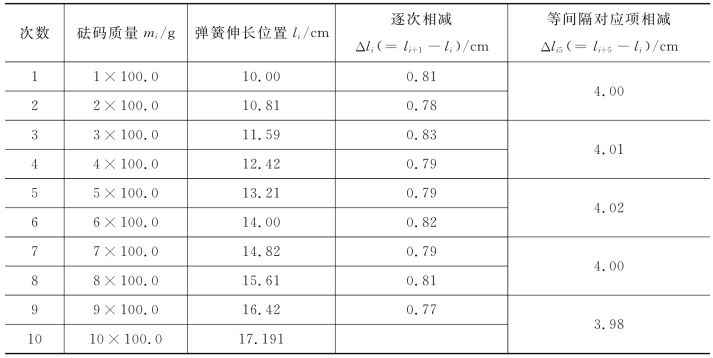
解 由逐次相减的数据可判出基本相等,验证了x与F之间的线性关系,且等距改变。
而求弹簧的劲度系数,则利用等间隔对应项逐差的结果,得序号1~5为前组,6~10为后组,再将两组数据中的l按对应顺序逐项相减:
l6-l1=4.00,l7-l2=4.01,l8-l3=4.02 l9-l4=4.00 l10-l5=3.98
则每隔5项差值的平均值为
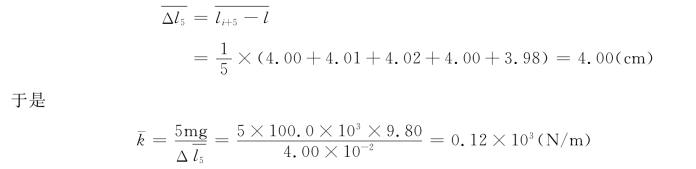
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




