大学物理实验：作图法简单直观，用于伏安法测量数据外推

作图法能将物理量之间的关系用图线表示出来，既简单又直观。有了图线以后，则可在图线范围内得到任意值对应的值（内插法）。在一定的条件下，也可以从图线的延伸部分得到测量数据以外的数据（外推法）。若不通过图线，要想获得以上数据还要做很多的计算或重新观测。此外，利用图线可求某些物理量（例如，图线为直线时，通过求截距和斜率，可求出有关物理量）。运用图解法还可由图线建立相应的经验公式。

1.作图规则

1）作图一律用坐标纸（直角坐标纸或对数坐标纸等）。坐标纸的大小和坐标轴的比例应根据所测数据的有效数字位数和结果的需要而定。原则是，测量数据中的可靠数字在图中应为准确的，最后一位存疑数字在图中应是估计的。即坐标纸的最小格对应测量数据中的最后一位可靠数字。

2）选轴。以横轴代表自变量，纵轴代表因变量，并画两条粗细适当的线表示横轴和纵轴。在轴的末端近旁注明所代表的物理量及单位，中间用逗号分开。对于每个坐标，在相隔一定的距离上用整齐的数字来标度。横、纵轴的标度可以不同，两轴的交点也可以不从零开始，而取比数据最小值再小些的整数开始标值，以便调整图线的大小和位置，使图线占据图纸的大部分区域而不偏于一角或一边。若数据特别大或特别小，可以提出乘积因子，并标在坐标轴上最大值的右面。

3）标点。根据测量数据，用削尖的铅笔在图上标出各测量数据点，并以该点为中心，用“+”“×”“⊙”等符号中的任一种标明。符号在图上的大小，由这两个物理量的最大绝对误差决定。同一图线上的观测点要用一种符号。如果图上有两条图线，则应用两种不同符号加以区别，并在图纸的空白处注明符号所代表的内容。

4）连线。除了画校正图线要把相邻两点用直线连接以外，一般连线时应尽量使图线紧贴所有的观测点而过（但应舍弃严重偏离图线的某些点），并使观测点均匀分布于图线的两侧。方法是：一面移动透明的直尺或曲线板，一面用眼注视着所有的观测点，当直尺或曲线板的某一段同观测点的趋向一致时，用削尖的铅笔连成光滑曲线。如欲将此图线延伸到观测数据范围之外，则应依其趋势用虚线表示。

5）写图名。在图纸顶部附近空白位置写出简洁而完整的图名。一般将纵轴代表的物理量写在前面，横轴代表的物理量写在后面，中间用符号“-”连接。在图名的下方允许附加必不可少的实验条件或图注。

2.解析法：求直线的斜率和截距

物理实验中遇到的图线大多数属于普通曲线，因此这些曲线大都可用一个方程式来表示。与图线对应的方程式一般称为经验公式。现在讨论实验图线为直线的情况。

设经验公式为y=a+bx，则该直线的斜率为

式中，（x1，y1），（x2，y2）分别为图中直线上两点的坐标，这两点不容许使用原观测点。若x轴起点为零，则可直接从图上读出截距a。若x轴起点不为零，则可在求出b后，再选图线上任一点（x3，y3）代入方程式中，即可求出截距a为

（x3，y3）点也不允许使用原观测点。应当指出，这是一种粗略地求a、b的方法。

例1-13 用伏安法测某导体线性电阻数据如表1-3所示，试用作图法求电阻。

表1-3　伏安法测某导体线性电阻数据(www.xing528.com)

解 1）描点法作图。图1-3是按上述方法和所测量数据作出的实验图线，即某导体的I-U图。由图1-3可知，物理量I与U呈线性关系。

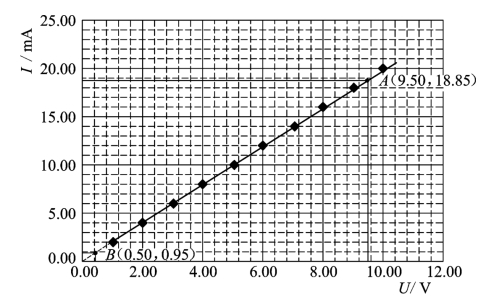
图1-3　I-U图

2）解析法求直线的斜率与截距。如图线为直线，可设此直线方程为

只要定出系数a和b（截距和斜率），则I与U的关系就确定了。为此我们在图上任找两点A（9.50，18.85）和B（0.50，0.95），这两点的距离尽可能远些，然后将这两点代入方程

18.85=a+b9.50

0.950=a+b0.50

联立解得 a=0.0004→0，b=1.9889mA/V。于是I与U的关系为

I=1.9889U

这个由实验数据用作图法回归的方程就是I和U的经验公式。则导体电阻

3）外推法。直线的斜率知道后，就可利用“外推法”求得测量范围以外的数据点。所谓“外推法”就是把图线向外延伸，对应于某一自变量值去求得函数值的方法。应注意的是：使用“外推法”时，必须假定物理关系在外延范围也是成立的。

作图拟合直线的方法基于描点连线，但是由实验点连线有一定的任意性，所以用作图法回归的经验公式精确性较差。同样，用作图法求得的电阻精确度也较差，计算误差没多大意义，只用有效数字粗略地表示测量结果就可以了。