测量不确定度概念的基本原理

不确定度是表征测量结果具有分散性的一个参数，它是被测物理量的真值在某个量值范围的一个评定。或者说，它是由于测量误差的存在而对被测量值不能确定的程度。不确定度反映了可能存在的误差分布范围，即随机误差分量和未定系统误差分量的联合范围。

测量结果的不确定度，一般来源于被测量的定义不完整；实现被测量定义的方法不理想；取样代表性不够；测量仪器计量性能的局限性；作为计量标准的值不准确或引用的数据和参量不准确；被测量值在表面上完全相同的条件下重复测量中的变化；环境条件的认识和掌握不完善；测量人员的人为因素等。分析不确定度时，要求对不确定度来源做到不遗漏、不重复和仔细分析大的不确定度分量，遗漏了不确定度会算小，重复了则不确定度会算大。

测量结果与很多量有关，所以不确定度来源于许多因素，这些因素对测量结果形成若干不确定度分量。因此，不确定度一般由若干分量组成。如果这些分量只用标准误差给出，称为标准不确定度，用符号u（通常带有作为序号的下角标）表示。按照评定方法的不同，标准不确定度可分为两类。

1.标准不确定度的分类

（1）A类标准不确定度uA的评定

用统计的方法评估的不确定称为不确定度的A类分量，用uA表达。用贝塞尔法计算A类标准不确定度时，就是直接对多次测量的数值进行统计计算，求其平均值的标准偏差。因此，在物理实验课的教学中，A类标准不确定度的计算方法如下：对被测量x，在相同条件下，测量n次，以其算术平均值作为被测量的最佳值。它的A类标准不确定度为

（2）B类标准不确定度uB的评定

全部误差中所有用非统计方法计算的分量为不确定度的B分量，以标准差uB表征。而B类标准不确定度常用估计方法，要估计适当，需要确定分布规律，需要参照标准，更需要估计者的学识水平、实践经验等。在实验中尽管有多方因素存在，为了简化，本课程中一般只考虑计量器具误差这一因素，以利于教学。

1）测量仪器的最大允许误差。任何测量都需借助一定的仪器或装置进行，任何仪器在制造或装配过程中都难免有一些缺陷，如轴承摩擦、游丝不匀、检测标准本身的误差等，即使在正确使用的情况下，这种缺陷也会带来误差，仪器误差或允许误差限就是在正确使用条件下，测量所得结果和被测量的真值之间可能产生的最大误差，它包含了在规定条件下可定系统误差、未定系统误差和随机误差的总效果。

生产厂家在制造某种仪器时，在其技术规范中预先设计、规定了最大允许误差（又称为极限允许误差、误差界限、允差等），终检时，凡是误差不超过此界限的仪器均为合格品。在物理实验课的教学中，测量仪器的最大允许误差通常用Δ仪表示。

仪器的Δ仪通常按以下方法确定：

a.有刻度的仪器，没标出精度（等级）取其最小分度的一半（没有说明书）；

b.绝对误差形式给出（说明书）；

c.以引用误差形式给出。

例如，量程为1mA、1.0级直流毫安表的Δ仪=±（1mA×1.0%）=±0.01mA。其中，“1.0”在表盘上表示。去掉引用误差的正负号及“%”后，成为仪器的准确度等级。其引用误差为0.01mA/1mA=1.0%。

又如数字式电压表的最大允许误差为Δ仪=±（级别%×读数+n×最低位数值）。其中n代表仪器固定项误差，相当于最小量化单位的倍数，只取1，2，3，…

例如，某台数字式电压表的级别为0.02，读数为1.1666V，n=2，则

Δ仪=±（0.02%1.1666+2×0.0001）V=±4.3×104V

许多计量仪器、量具的误差产生原因及具体误差分量的计算分析，大多超出了本课程的要求范围。为使初学者方便，仅从以上3个方面来考虑仪器误差Δ仪。

物理实验常用仪器仪表的仪器误差如表1-1所示。

表1-1　物理实验常用仪器仪表的仪器误差

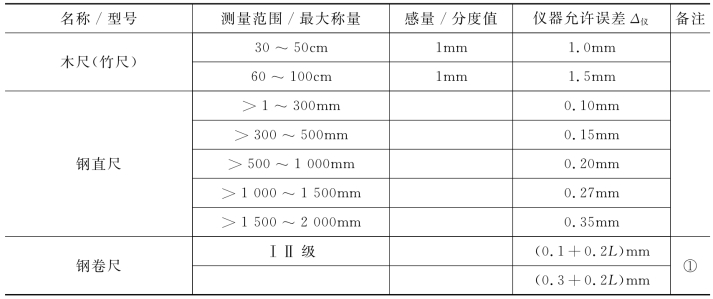
续表

注：①式中L是以米为单位长度，当长度不是米的整数倍时，取最接近的较大的整“米”数。

②千分尺有零级和一级两种。物理实验室使用的是一级，其示值误差需根据测量范围来确定。

③物理天平仪器误差的组成较为复杂，与天平的灵敏度或感量、称量载荷（或砝码）有关，还与不等臂引起的误差有关。为了简化，在物理实验中约定Δ仪=最小分度值的一半，也可约定Δ仪=感量电子天平的仪器误差。

④机械停表一般分度值为0.1s，Δ仪=0.1s。停表的人体反映误差大约为0.2s，可归并到仪器误差中，故使用停表时可取=0.3s；对于石英电子秒表，其最大偏差（15.8×10-6t+0.01）s，其中t是时间的测量值。在本课程中对较短时间测量可按0.01s作为电子秒表的仪器误差。

⑤水银温度计分为全浸式与局浸式两种，后面仪器误差为量程100～200℃；一等标准水银温度计分度值0.05℃，Δ仪=0.1℃。(www.xing528.com)

⑥如电流、电压表等指针式电表。

⑦R为电阻示值，α为准确度等级，m为所用转盘数，b为与等级有关的常数。

⑧α为准确度等级；x为示值；Un、Rn为基准值（等于有效量程内最大的10的整数次幂，即10n≤有效量程，n=0，±1，±2，…），有时也可简化地写为Δ仪=xα/100。

⑨α为准确度等级；x为示值；b为某个常数，称为误差的绝对项系数；Nx为仪表的满刻度值；d为仪器固定项误差，相当于最小化单位的倍数，只取1，2，3，…数字。

2）B类标准不确定度的估计。在物理实验课的教学中，B类标准不确定度的估计方法是：

a.对误差服从正态分布（误差限对应0.9973的置信概率）的仪器，B类标准不确定度为

一般来说，仪器的误差在[-Δ仪，Δ仪]范围内是按一定的概率分布的。在相同的条件下大批量生成的产品，其质量指标一般服从正态分布。由正态分布函数的性质可以知道，误差大于极限误差的概率不超过0.3%，所以质量指标服从正态分布的产品，单次测量的B类不确定度可以记为uB。一般而言uB与Δ仪的关系为

b.对误差服从均匀分布（误差限对应0.577的置信概率）的仪器，B类标准不确定度为

所谓均匀分布是指在测量值的某一范围内，测量结果取任一可能值的概率相等，而在该范围外的概率为零。若对某类仪器的分布规律一时难以判断，可近似按均匀分布处理。在本物理实验课教学中，一般规定：除非另有说明，均按均匀分布处理。

不确定度的两种评定方法都基于概率分布，并都用方差或标准差表征。不确定度的分类方法与误差分类相比，避免了由于误差之间的界限不绝对，在判断和计算时不易掌握的缺点。评定不确定度时，不考虑影响不确定度因素的来源与性质，只考虑评定方法，从而简化了分类，便于评定与计算。

2.合成标准不确定度

如上所述，在测量结果的质量评定中，标准不确定度有两类分量，即由统计方法得到的A类不确定度分量和由其他方法获得的B类不确定度分量。如果这些分量是相互独立的，即不相关的，由各标准不确定度分量合成而来的标准不确定度称为合成标准不确定度，即合成标准不确定度等于各标准不确定度分量的平方和的根（方和根法）：

3.总不确定度（扩展标准不确定度）

合成不确定度uC对应于标准差测量结果x±uC含真值的概率为68.3%。总标准不确定度是确定测量结果分散区间的参数。它所给出的置信空间有更高的置信水平，常用标准不确定度的k倍数表示，即扩展标准不确定度由合成标准不确定度乘以因子k得出。用U代表扩展标准不确定度，则有

式中，k为包含因子或覆盖因子，它把合成标准不确定度扩展了k倍。在物理实验课的教学中取k=1区间的置信概率为68.3%（不再强调）；在大多数情况下，当k=2时区间的置信概率为95.5%，k=3时区间的置信概率为99.7%。

4.相对不确定度

s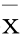（）与Δ仪均未考虑待测量的大小，表征的是测量的离散度，但不能表征测量结果接近真值的程度，因此合成不确定度不足以表征测量结果的优劣。为评价测量的优劣，常用相对不确定度表示，且

如果待测量有理论值或公认值，则可用百分比误差来表示测量的优劣，且

式中，x0为理论值或公认值。

注意：百分误差只能用来表示测量的优劣，而不能表示测量结果的统计意义。显然E与E0都没有单位，只是一个比值。

所以，对测量结果完整表示时，应在用合成不确定度表示不确定范围的同时再用相对不确定度表示测量结果的优劣。