提高Web服务组合可靠性的隐马尔可夫服务模型

隐马尔可夫服务模型利用服务行为描述和历史数据构建诊断模型，根据设定的权重将两种诊断信息合并。由于实际中服务行为描述具有不完备性以及历史数据中包含噪声数据，因此两种诊断信息的合并能够弥补单类信息不完备的问题，完善系统模型，提高诊断的准确性。

隐马尔可夫服务模型主要是借用隐马尔可夫模型的思想，将服务中的行为执行序列转化为行为转移概率矩阵，将服务中的消息执行序列转化为消息转移概率矩阵，以及将行为与其输出之间的依赖关系转化为观察概率矩阵。

定义4.38　隐马尔可夫服务模型是六元组SHM=（B，M，π，BM，MM，OM），其中：

（1）B表示一组行为集合，B={b1，b2，…，bn}，其中n表示在服务中行为的个数；

（2）M表示一组可观察到的输出的消息集合，M={m1，m2，…，mk}，其中k表示输出消息的个数；

（3）π表示初始状态分布，π={πi，1≤i≤n}，πi=P（X1=bi），其中X1表示初始执行的行为；

（4）BM表示行为转移矩阵，BM={bpij，1≤i，j≤n}，bpij=P（Xt+1=bj|Xt=bi），其中bpij表示从第i个行为到第j个行为的转移概率，Xt表示t时刻执行的行为，且；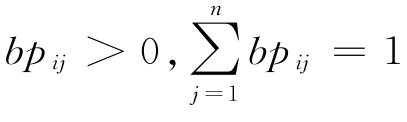

（5）MM表示消息转移矩阵，MM={mpij，1≤i，j≤k}，mpij=P（Yt+1=mj|Yt=mi），其中mpij表示从第i个消息到第j个消息的转移概率，Yt表示t时刻输出的消息，且；

（6）OM表示观察矩阵，OM={opij，1≤i≤n，1≤j≤k}，opij=P（Yt=oj|Xt=bi），其中opij表示第i个行为输出第j个消息的概率，oj表示第j个消息，Yt表示t时刻输出的消息，Xt表示t时刻执行的行为。

4.5.3.1　建模服务行为描述

对于Web服务行为描述而言，行为转移矩阵描述的是所有可能的正常的行为执行序列，类似地，消息转移矩阵描述的是所有可能的正常的消息输出序列，而观察矩阵描述的是所有执行行为与其可能的输出消息之间的正常依赖关系。由于行为描述中所有执行序列都具有相同的发生概率，所以行为描述中所有从同一行为转移的行为转移序列具有相同的转移概率，行为描述中所有从同一消息转移的消息转移序列具有相同的转移概率，而行为描述中所有从同一行为输出的观察序列也都具有相同的概率。

定义4.39　一个行为描述的行为转移矩阵BM1={bpij，1，1≤i，j≤n}，这里：

（1）对于任意的行为bi和bj，1≤i，j≤n，如果在行为描述中存在（bi，bj）的行为转移序列，那么n（bi，bj）=1，否则n（bi，bj）=0；

定义4.40　一个行为描述的消息转移矩阵MM1={mpij，1，1≤i，j≤k}，这里：

（1）对于任意的消息mi和mj，1≤i，j≤k，如果在行为描述中存在（mi，mj）的消息转移序列，那么n（mi，mj）=1，否则n（mi，mj）=0；

(2)。

定义4.41　一个行为描述的观察矩阵OM1={opij，1，1≤i≤n，1≤j≤k}，这里：

（1）对于任意的行为bi和任意的消息mj，1≤j≤k，如果在行为描述中的行为bi能够输出消息mj，那么n（bi，mj）=1，否则n（bi，mj）=0；

(2)。

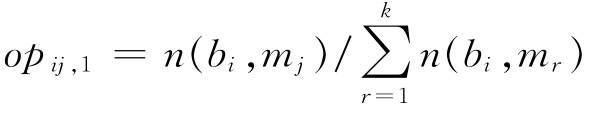4.5.3.2　建模历史数据

对于Web服务的历史数据，我们做了如下假设：

（1）历史数据中记录的是正常的执行序列，或可以根据执行结果来判断执行序列的执行情况，以便于选取所有正常执行的序列进行建模；

（2）历史数据中每个执行序列都记录了执行的行为以及行为输出的消息；

（3）历史数据集合用hd来表示，且hd={esqi，1≤i≤l}，l表示数据集hd中执行序列的个数；

（4）历史数据集合hd中的每条执行序列esqi=＜o1，o2，…，oT＞，T表示该执行序列执行的行为个数，ot=（bi，mj）表示执行序列中第t个执行的行为是bi且其输出的消息是mj；

（5）执行序列中的每个观察值ot=（bi，mj），1≤t≤T，1≤i≤n，1≤j≤k。(www.xing528.com)

定义4.42　一个历史数据集合hd的行为转移矩阵BM2={bpij，2，1≤i，j≤n}，这里：

（1）对于任意的1≤i，j≤n，n（bi，bj）表示在数据集合hd中从行为bi转移到行为bj的个数；

(2)。

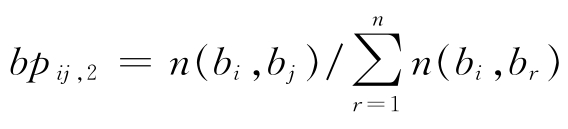定义4.43　一个历史数据集合hd的消息转移矩阵MM2={mpij，2，1≤i，j≤k}，这里：

（1）对于任意的1≤i，j≤k，n（mi，mj）表示在数据集合hd中从消息mi转移到消息mj的个数；

(2)。

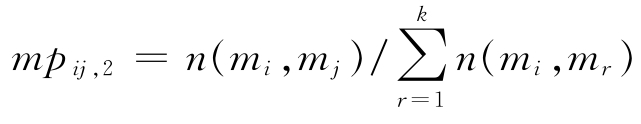定义4.44　一个历史数据集合hd的观察矩阵OM2={opij，2，1≤i≤n，1≤j≤k}，这里：

（1）对于任意1≤i≤n，1≤j≤k，n（bi，mj）表示在数据集合hd中行为bi输出消息mj的个数；

(2)。

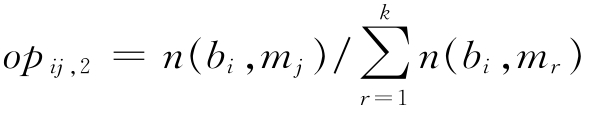4.5.3.3　构建服务模型

对于隐马尔可夫模型而言，它的行为转移矩阵、消息转移矩阵以及观察矩阵就是将通过行为描述和历史数据构建的两组相同的矩阵按照一定的权重合并。对于行为描述的权重w1和历史数据的权重w2在这里并不做具体说明，可根据实际情况确定，但是两个权重值之和必须等于1，即w1+w2=1。如果历史数据较多，能够覆盖大部分正常执行情况，且行为描述相对完备，那么可以设置w1=w2=0.5；如果历史数据较多，而行为描述不太完备，那么可以设置w1＜w2；再如历史数据较少，而行为描述相对完备，那么可以设置w1＞w2。

定义4.45　一个服务模型的行为转移矩阵BM={bpij，1≤i，j≤n}，这里：

(1)bpij=w1bpij，1+w2bpij，2；

（2）w1表示行为描述在模型中所占的权重，w2表示历史数据在模型中所占的权重。

定义4.46　一个隐马尔可夫混合模型的消息转移矩阵MM={mpij，1≤i，j≤k}，这里：

(1)mpij=w1mpij，1+w2mpij，2；

（2）w1表示行为描述在模型中所占的权重，w2表示历史数据在模型中所占的权重。

定义4.47　一个服务模型的观察矩阵OM={opij，1≤i≤n，1≤j≤k}，这里：

(1)opij=w1opij，1+w2opij，2；

（2）w1表示行为描述在模型中所占的权重，w2表示历史数据在模型中所占的权重。

定义4.48　一个消息观察序列σ={o1，o2，…，oT}，这里：

（1）T表示在消息观察序列σ中行为及其输出消息的个数；

（2）ot表示观察序列中第t个执行的行为及其输出的消息，1≤t≤T。

这里需要说明两点：①对于服务中的并发执行序列，由于观察序列是一个顺序序列，并发执行的行为及其输出的消息也是按观察到的顺序记录的，因此在使用行为描述建模时，对于并发结构的行为不仅要考虑行为描述中定义的正常行为及消息转移序列，而且还要考虑并发执行序列间的转移情况，即对于包含m个执行序列的并发结构中的第l个执行序列中的第i个行为bi及其输出消息。这里τ表示第l个执行序列中的第i+1个行为bi+1或其输出消息mi+1，或表示并发结构中除第l个执行序列以外的其他任何一个执行序列中的任何一个行为或消息；nbj表示第j个执行序列中行为的个数；nmj表示第j个执行序列中消息的个数。②对于服务中的循环执行序列，在观察序列中则是按照执行的次数记录的，因此在诊断时只考虑一次循环。