Matlab谱方法高效解二维平流-扩散方程

第4章给出了在周期性边界条件下求解二维平流-扩散方程的方法，本小节将在狄利克莱边界条件下求解该方程，有兴趣的读者可以比较它们之间的差异。

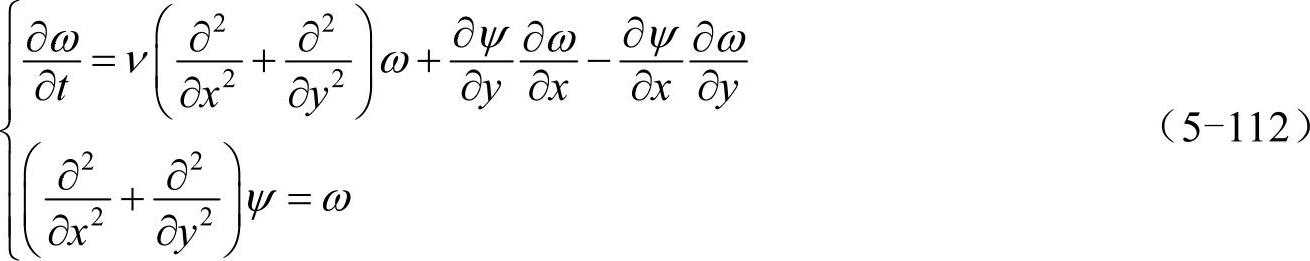
上式为二维平流-扩散方程，其中，ψ、ω分别是流函数和涡量，x、y为空间坐标，t是时间，v为常数。计算区域Ω为：-10＜x,y＜10，边界条件为ψ|∂Ω=ω|∂Ω=0。用切比雪夫点在计算区域Ω内将函数ψ、ω离散化为N+1阶方阵ψ(N+1)×(N+1)、ω(N+1)×(N+1)。式（5-112）的第一式等号左边的∂ω/∂t可用ode45函数计算，等号右边可表示为矩阵形式（“~”代表删除首尾行首尾列的操作）：

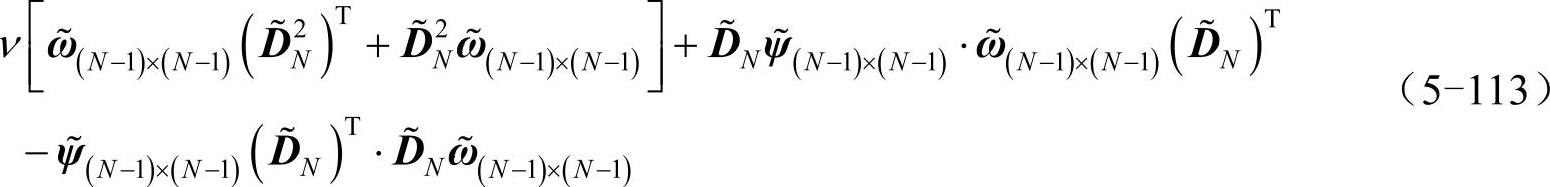
将函数ψ、ω的离散形式由方阵写为向量，并根据式（5-34）所示的拉普拉斯算符矩阵形式，式（5-112）的第二式可表为：

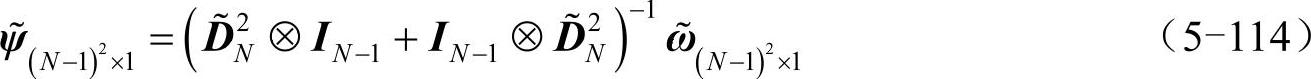
取v=0.001，初始条件ω(x,y,0)=sech[(x+2)2+y²/20]+sech[(x-2)2+y²/20]，求解式（5-112）代码如下：

程序5-29

主程序代码如下：(www.xing528.com)

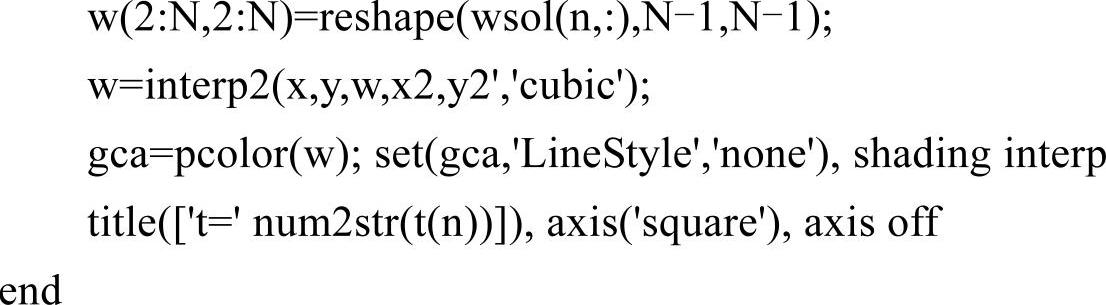
文件advection_diffusion.m代码如下：

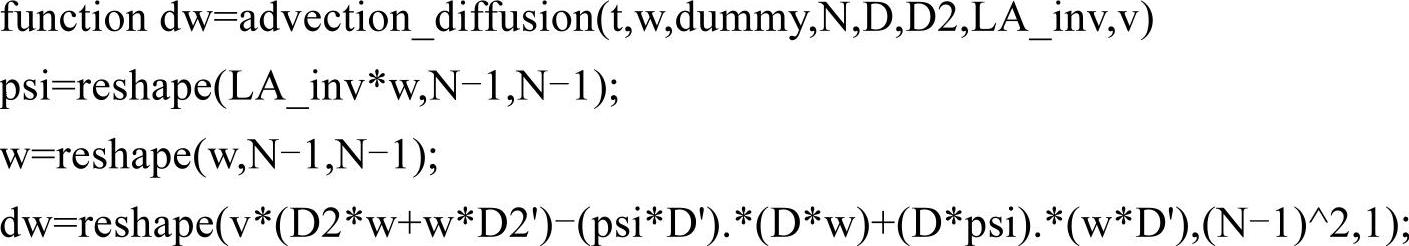
程序中的拉普拉斯算符矩阵为(N-1)2阶方阵，它的求逆运算将耗费相当多CPU和内存资源。为节约时间，主程序仅对其做一次求逆运算，每次调用advection_diffusion函数时，将其逆矩阵作为参数传递进去。即使这样，执行本程序的时间仍然比本书中的其他程序略多一些。此外，因为计算时删除了方阵ψ(N+1)×(N+1)、ω(N+1)×(N+1)在边界处的值，所以最后要在相应位置补0。又因为依照切比雪夫点划分计算区域Ω导致计算结果在空间上的不均匀分布，所以最后使用了interp2函数对结果进行插值使其均匀化。最终结果如图5-34所示。

图5-34 狄利克莱边界条件下的二维平流-扩散方程的计算结果