高效实现：Matlab谱方法求解二维Barkley模型

在前面章节关于含时问题的实例中，使用了ode45处理函数u对时间t的导数∂u/∂t。ode45是基于4、5阶龙格-库塔法的变步长算法，可以根据所计算方程变化的快慢自行调整步长，在保证误差符合要求的前提下尽可能快地求解问题。但需要将u的边界条件转化为针对∂u/∂t的边界条件，这往往要求u的二阶混合偏导数∂²u/∂t∂x可以交换求导顺序。实际上，为避免这一不便，还可以使用欧拉法处理导数∂u/∂t，但同时带来了如下问题：运算量大，精度低，代码略繁，需要人为选取合适的步长。变步长的4、5阶龙格-库塔法和欧拉法各有利弊，选取哪种方法应根据问题具体情况、计算机配置和个人喜好来决定。

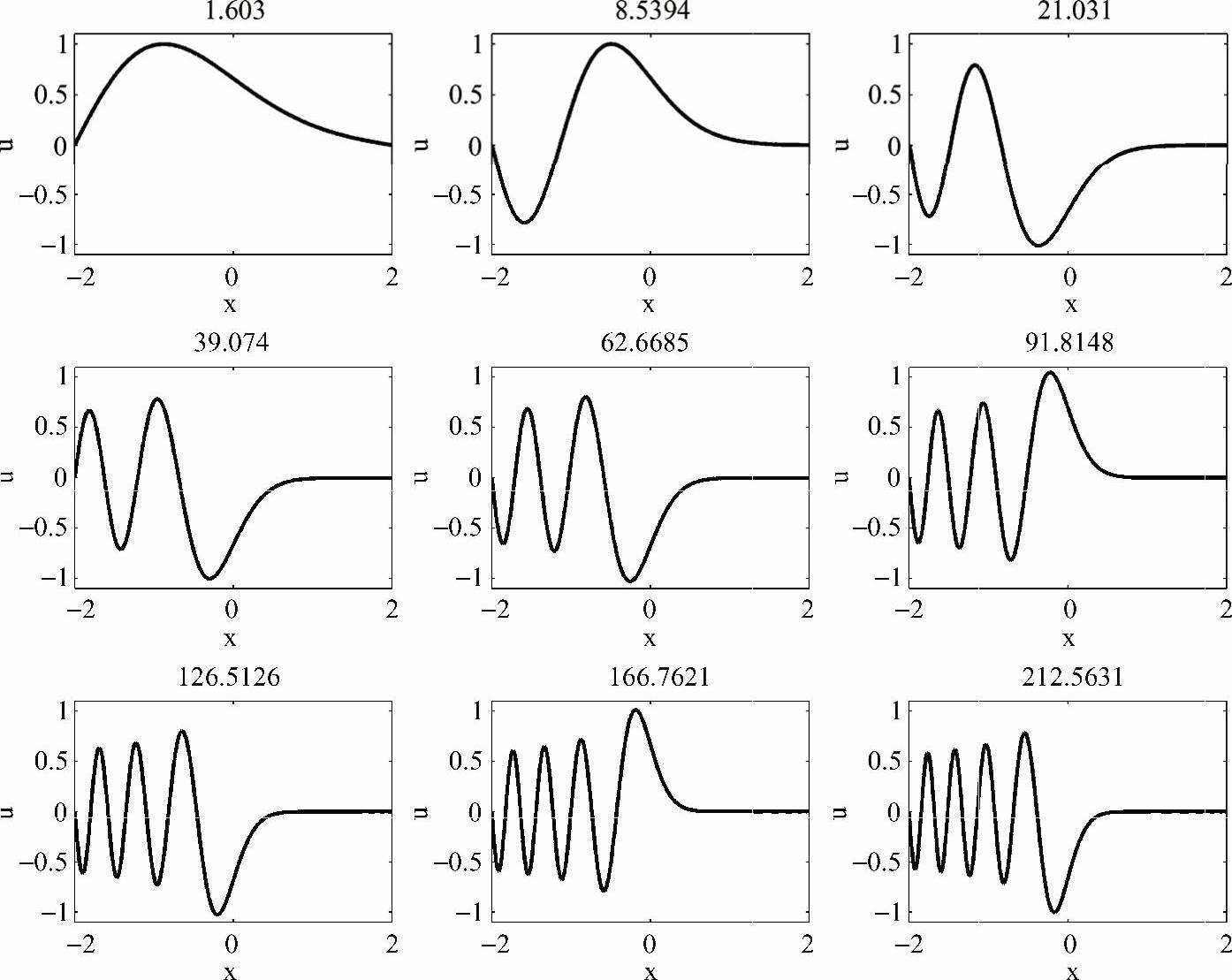
图5-32 广义特征值问题的前9个特征值和特征向量

下面以数值计算反应-扩散系统中的螺旋波为例讲解如何用欧拉法解决含时问题。螺旋波是系统远离平衡态时由于系统自组织形成的一类特殊斑图。在B-Z反应、正在聚集的粘性霉菌、铂金表面的一氧化碳氧化以及心脏中均能观测到螺旋波的存在。描述螺旋波的Barkley模型为：

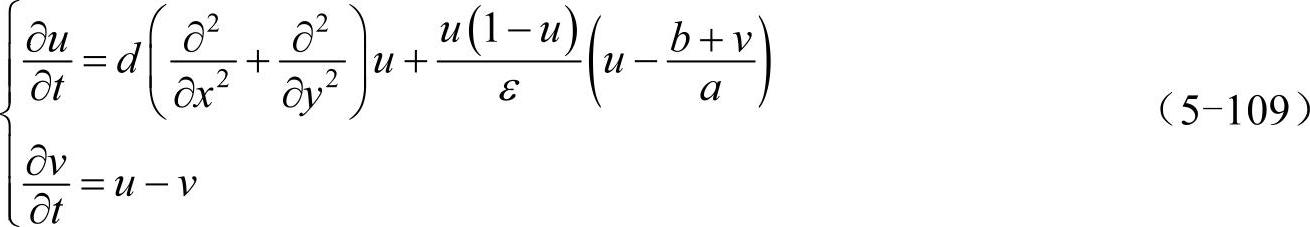
其中，u和v是2种能够相互转化的化学物质的浓度，t为时间，x、y为空间坐标，d为扩散系数，a、b和ε为系统参数。

根据欧拉法，∂u/∂t和∂v/∂t表示为：

在二维区域的切比雪夫点上将函数u、v离散化为N+1阶方阵u(N+1)×(N+1)、v(N+1)×(N+1)。利用切比雪夫求导矩阵处理方程中的扩散项(∂²/∂x²+∂²/∂y²)u，即：(https://www.xing528.com)

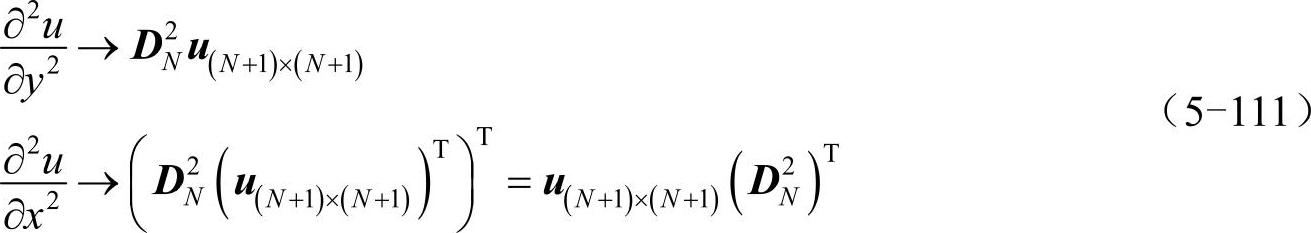
选取计算区域Ω为：-60<x,y<60。由于化学物质在边界处没有进出，所以边界条件为∂u/∂n|∂Ω=∂v/∂n|∂Ω=0（n代表边界∂Ω处的法向），可根据式（5-69）处理该诺依曼边界条件。参数取值为：a=0.5，b=0.01，d=1.6，ε=0.02。为产生螺旋波，需要将两种化学物质浓度u、v的初始状态设置为在空间上具有3个不同值0、0.5、1的浓度梯度的状态，具体参见代码。

程序5-28

代码中选取的时间步长为0.002，每前进一步，都要根据边界条件修正u、v在边界处的取值。程序每隔5个单位时间输出一幅小图，如图5-33所示。

图5-33 螺旋波的产生过程