【摘要】：而广义特征值问题的形式为：Au=λBu 其中，A和B为已知方阵，u为未知非零向量，λ为未知常数。使上式成立的λ称为特征值，相应的向量u称为特征向量。求解广义特征值问题通常选用QZ法，在Matlab中的调用形式为eig(A,B)。则式的矩阵形式为：对于这样的广义特征值问题，求解代码如下：程序5-27程序输出了前9个正特征值及相应的特征向量，如图5-32所示。
标准的特征值问题形如下式：
Au=λu （5-104）
其中，A为已知方阵，u为未知非零向量，λ为未知常数。使上式成立的λ称为特征值，相应的向量u称为特征向量。可用Matlab的eig函数求解上述问题的特征值和特征向量，调用形式为eig(A)。
而广义特征值问题的形式为：
Au=λBu （5-105）
其中，A和B为已知方阵，u为未知非零向量，λ为未知常数。使上式成立的λ称为特征值，相应的向量u称为特征向量。若方阵B可逆，广义特征值问题可化为式（5-104）的形式，即：
B-1 Au=λ u （5-106）
但这么做既不简单也不实用，况且方阵B也未必是可逆的。求解广义特征值问题通常选用QZ法（QZ method），在Matlab中的调用形式为eig(A,B)。以下面的特征值问题为例：(www.xing528.com)
u′′=λxu,-2<x<2,u(±2)=0 （5-107）
用N+1维向量u(N+1)×1代表函数u(x)在区间[-2,2]上的切比雪夫点x=(x0,x1,…,xN)T处的取值，删去其首尾元素得到N-1维向量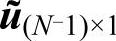
。则式（5-107）的矩阵形式为：
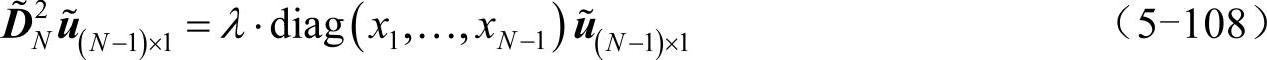
对于这样的广义特征值问题，求解代码如下：
程序5-27
程序输出了前9个正特征值及相应的特征向量，如图5-32所示。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
