Matlab高效解法：二维热传导方程

若两个边界分别采用洛平边界条件(u+hu′)|_x=1=0(h≠0)和诺依曼边界条件u′|_x=-1=0，即：

设函数u(x)在切比雪夫点x=(x₀,x₁,…,x_N)T处的取值为向量u=(u₀,u₁,…,u_N)^T。与5.4.3小节的过程类似，整理可得(u₀,u_N)^T与(u₁,u₂,…,u_N-1)^T的关系：

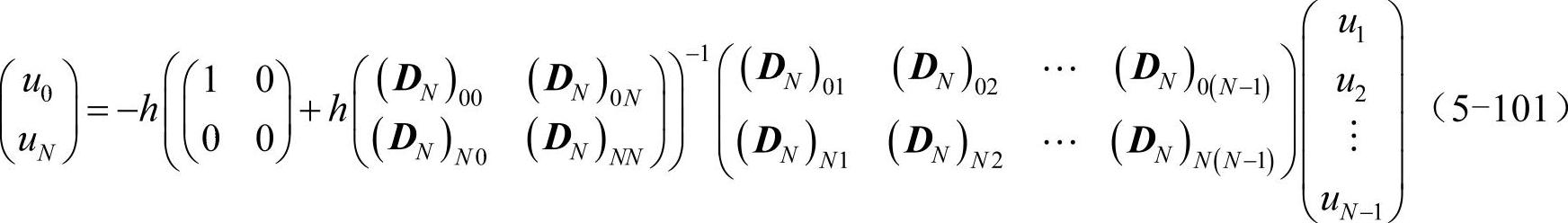
这样就把边界条件(u+hu′)|_x=1=0和u′|_x=-1=0转化为对u₀和u_N的约束条件，后面将用到这一关系。

式（5-102）描述了二维热传导问题，边界x=1处的洛平边界条件代表该边界是自由冷却的，边界x=-1和边界|y|=1处的诺依曼边界条件代表这些边界是绝热的。

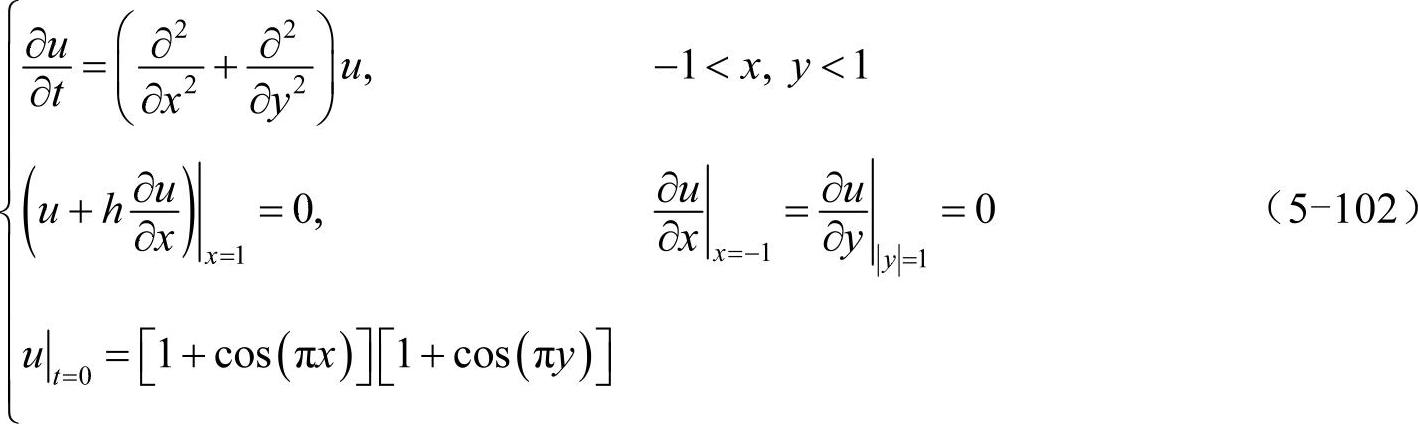
与一维热传导方程类似，为了能用ode45函数处理此问题，将上式等价写为：

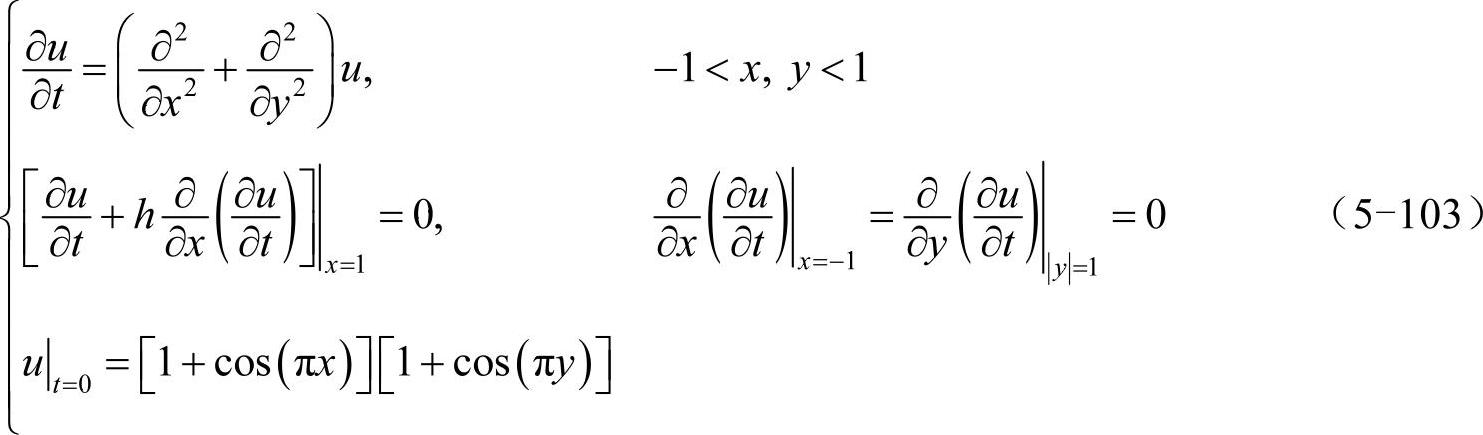
根据式（5-101）处理边界x=±1处的洛平边界条件和诺依曼边界条件，根据式（5-69）处理边界y=±1处的诺依曼边界条件（处理时需要将∂u/∂t看做u）。取h=0.1，代码如下：(www.xing528.com)

程序5-26

主程序代码如下：

文件heat2D.m代码如下：

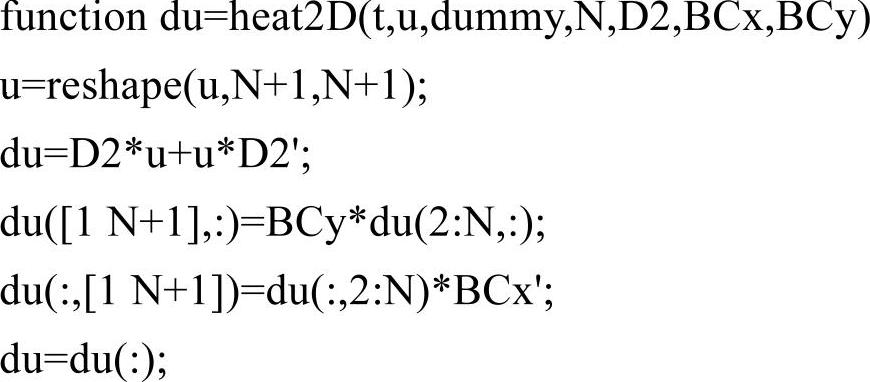
计算结果如图5-31所示，热量从中央的高温部分流向四周的低温部分。因为热量只能通过边界x=1传递到外界，而其他3个绝热边界处都积累了热量，所以温度普遍比边界x=1处高。若时间t足够长，各处温度将趋于0。此外，数值解在边界x=1处的最大误差在10^-14数量级。

图5-31 1个边界自由冷却、其他3个边界绝热的二维热传导问题的解