Matlab微分方程高效解法：一维热传导方程的谱方法

在分析一维热传导方程的解法前，先把洛平边界条件写为矩阵形式。这里以洛平边界条件(u±hu′)|_x=±1=0为例，其中的正号对应右边界，负号对应左边界。那么可将其写为：

设函数u(x)在切比雪夫点x=(x₀,x₁,…,x_N)T处的取值为向量u=(u₀,u₁,…,u_N)T。则有：

将式（5-95）和式（5-68）代入式（5-94），整理可得(u₀,u_N)T与(u₁,u₂,…,u_N-1)T的关系：

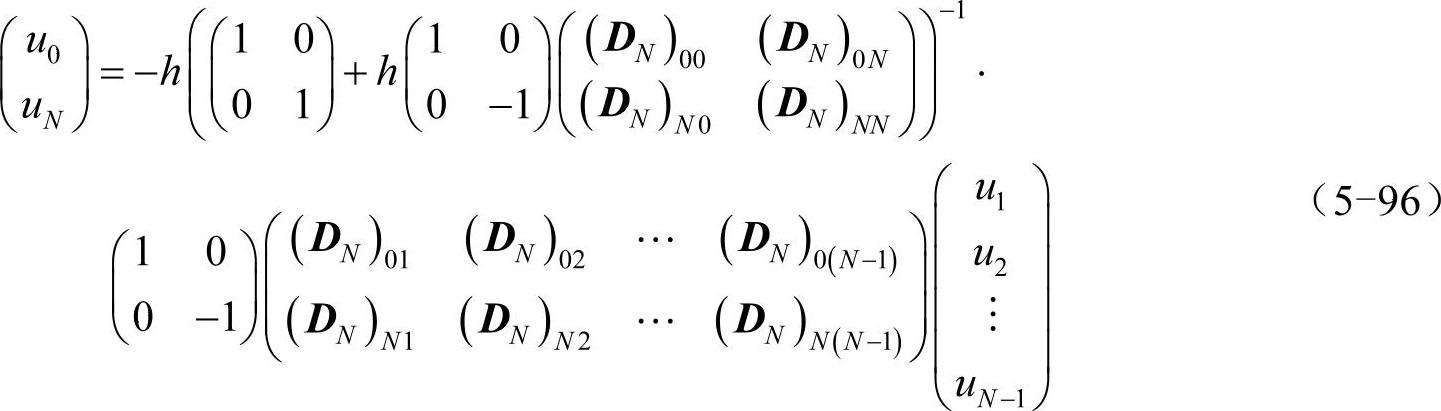
至此，洛平边界条件(u±hu′)|_x=±1=0被转化成了对u₀和u_N的约束条件（5-96），该式可用程序容易地计算。处理(u±hu′)|_x=±1≠0的情况与之类似，不再赘述。

下面讨论一维热传导方程：

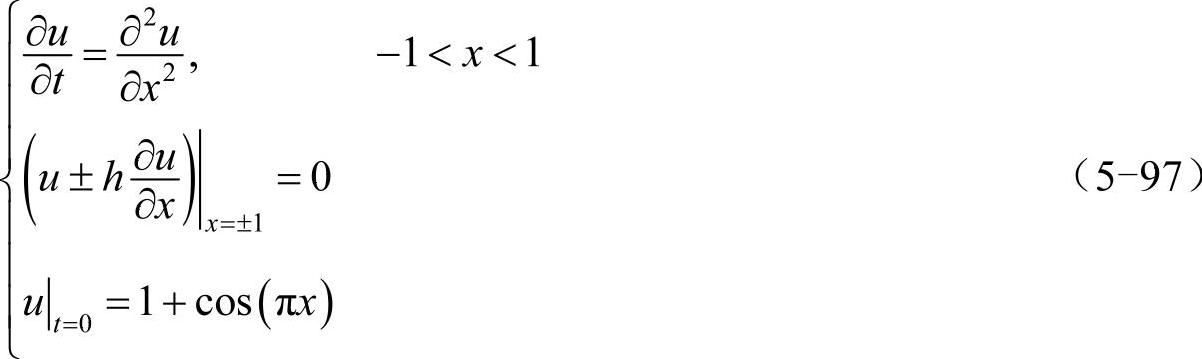
上式描述了均匀细杆上的热传导过程，u代表温度分布，t代表时间，x代表杆上的坐标，洛平边界条件代表杆在边界处是自由冷却的。所谓自由冷却，是指杆的两端与周围环境根据牛顿冷却定律交换热量，即单位时间单位横截面积从边界处释放的热量与边界和外界的温度差成正比。由此可以得到(u±h∂u/∂x)|_边=v，其中v为外界温度，h为一常数，正负号分别对应于右边界和左边界。可以预料，若时间t足够长，杆上的温度将处处趋于v。

根据方程的物理意义可知，∂u/∂t|_边和∂(∂u/∂x)/∂t|_边均是连续变化的，则u对x和t的二阶混合偏导数可以交换求导顺序（证明从略），即∂(∂u/∂x)/∂t=∂(∂u/∂t)/∂x。所以式（5-97）的边界条件可等价写为：

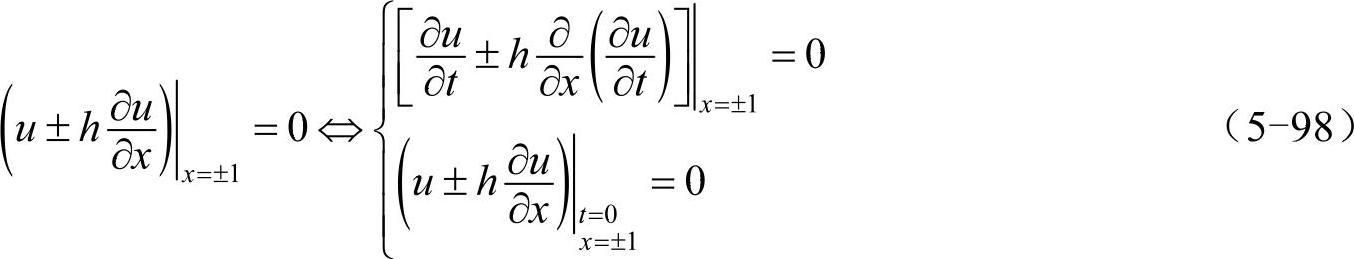
则式（5-97）可被转化为如下形式：(www.xing528.com)

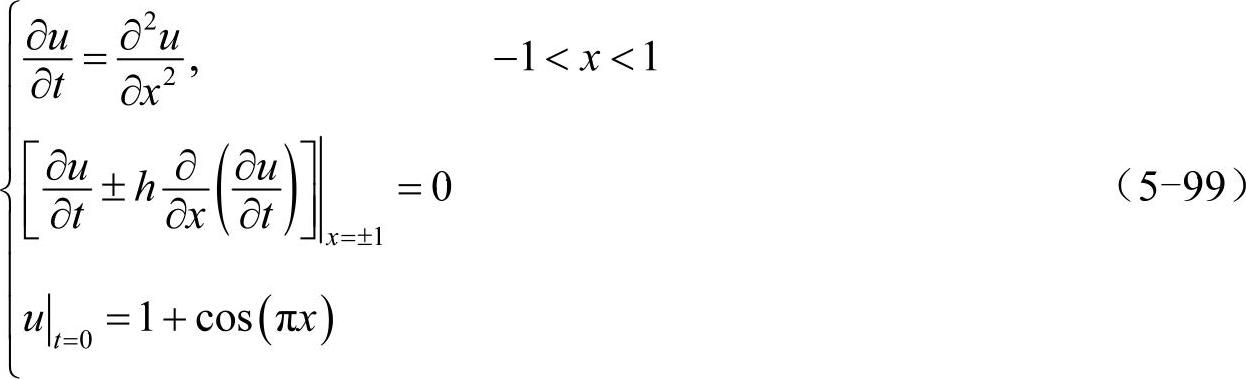
接下来就可以利用ode45函数计算上式，根据式（5-96）处理其中的边界条件（处理时需要将∂u/∂t看做u）。取h=0.1，代码如下：

程序5-25

主程序代码如下：

文件heat1D.m代码如下：

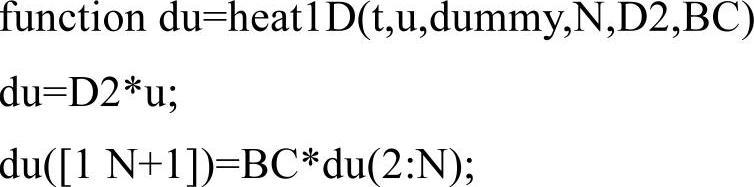
输出结果如图5-30所示，热量迅速在杆上扩散开来，并通过边界传递到外界，杆两端与外界的温差越小，向外界传递热量的速度也就越慢，最终整个杆的温度将趋于0。数值解在边界处的最大误差为3.5111×10^-15。

图5-30 两端边界自由冷却的一维热传导问题的解