【摘要】:考虑具有洛平边界条件的一维泊松问题:先将x和u分别离散化为N+1维向量x=(x0,x1,…那么,求解式,只需:在切比雪夫求导矩阵上乘以缩放因子可将上述方法推广至任意区间,以下面的一维泊松方程为例:根据式求解,并与其解析解u=ex+3x/4-3e-2+1比较,代码如下:程序5-23程序输出结果如图5-28所示:左图中,点表示计算得到的数值解,线表示解析解,二者吻合得很好。图5-28 左图:洛平边界条件下一维泊松问题的数值解(点)和解析解(线),右图:误差分布
考虑具有洛平边界条件的一维泊松问题:
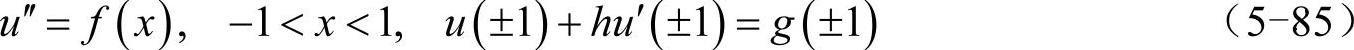
先将x和u分别离散化为N+1维向量x=(x0,x1,…,xN)T和u=(u0,u1,…,uN)T。针对两端边界的洛平边界条件,需要综合图5-8及图5-20所示的方法修改矩阵DN2。如图5-27所示:取出矩阵hDN的首(尾)行,在其首(尾)元素上加1,然后替换到矩阵DN2的首(尾)行处。这样修改后的矩阵DN2与向量u相乘所得向量的首尾元素将是u0+hu′(x0)和uN+hu′(xN)。
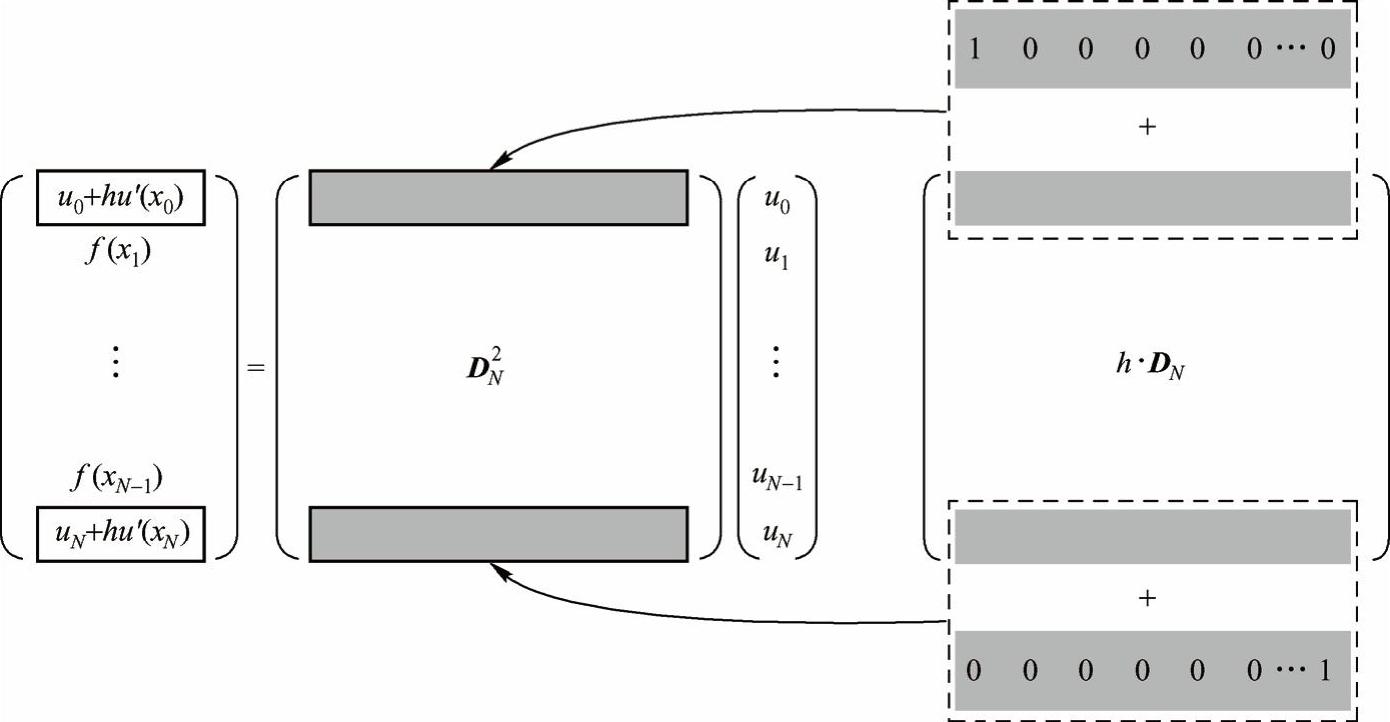
图5-27 在洛平边界条件下修改切比雪夫求导矩阵
在DN2上加两个“-”代表经过上述修改的切比雪夫求导矩阵,在f上加两个“-”代表将向量f=(f(x0),f(x1),…,f(xN))T的首尾元素分别替换为u0+hu′(x0)和uN+hu′(xN)的值(洛平边界条件)。那么,求解式(5-85),只需:

在切比雪夫求导矩阵上乘以缩放因子可将上述方法推广至任意区间,以下面的一维泊松方程为例:(https://www.xing528.com)
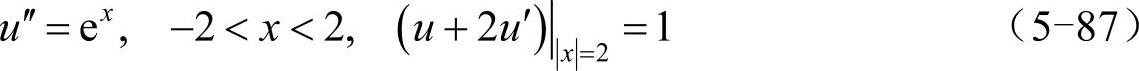
根据式(5-86)求解,并与其解析解u=ex+3(e-2-e2)x/4-3e-2+1比较,代码如下:
程序5-23

程序输出结果如图5-28所示:左图中,点表示计算得到的数值解,线表示解析解,二者吻合得很好。右图为误差分布,N=18时,最大误差仅在10-13级。
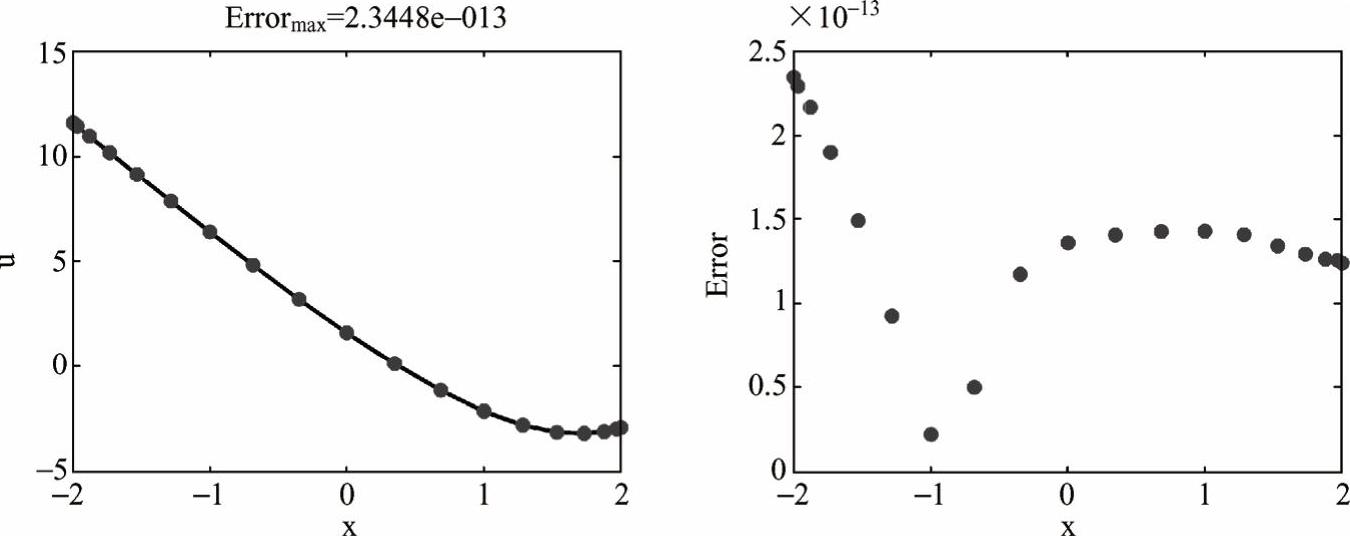
图5-28 左图:洛平边界条件下一维泊松问题的数值解(点)和解析解(线),右图:误差分布
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




