Matlab高效解法：谱方法解一维四阶问题

一维双调和问题（biharmonic problem）的形式如下：

u′′′′=f(x),-1<x<1,u(±1)=u′(±1)=0 （5-76）

求解上式的难点在于边界条件既规定了u(±1)=0同时又要求u′(±1)=0。为了简化这一复杂的边界条件，将u(x)的插值函数p(x)写为：

p(x)=(1-x²)q(x)，-1<x<1 （5-77）其中，q(x)在边界处取值为0，即q(±1)=0。容易知道，上式定义的p(x)必满足p(±1)=p′(±1)=0。这样就将插值函数p(x)的复杂边界条件简化为p(x)的狄利克莱边界条件。

对式（5-77）求4阶导数并代入q(x)=p(x)/(1-x²)，得：

那么，对p(x)求4阶导数的运算可写为矩阵形式：

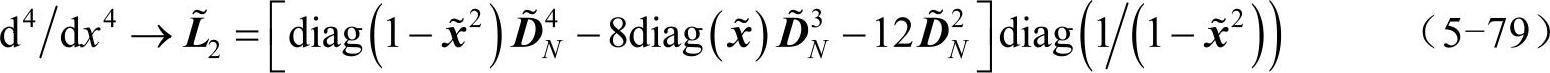
其中，函数diag表示将向量转化为对角矩阵，向量x代表(x₀,x₁,…,x_N)T。此外，向量1-x²代表(1-x²₀,1-x²₁,…,1-x_N²)T，向量1/(1-x²)代表(1/(1-x²₀),1/(1-x²₁),…,1/(1-x_N²))T。“~”表示删除向量的首尾元素以及删除矩阵首尾行、首尾列。根据式（5-79），可将式（5-76）写为矩阵形式：

求解上式只需求解：

(www.xing528.com)

并在得到的向量ũ的首尾补0。

以下面的双调和方程为例：

u′′′′=sin(πx),-1<x<1,u(±1)=u′(±1)=0 （5-82）

接下来求它的数值解，并与其精确解u=sin(πx)/π⁴+(x³-x)/2π³比较。代码如下：

程序5-21

结果如图5-25所示，N=24时的最大误差在10^-15数量级。

图5-25 左图：双调和方程的数值解（点）和解析解（线）；右图：误差分布

类似地，若双调和问题（5-76）的计算区间为[-L/2 L/2]，只需将式（5-77）中的1-x²改为L²/4-x²，并对D_N做相应的缩放即可。