Matlab谱方法高效解二维泊松方程

考虑如下二维泊松方程：

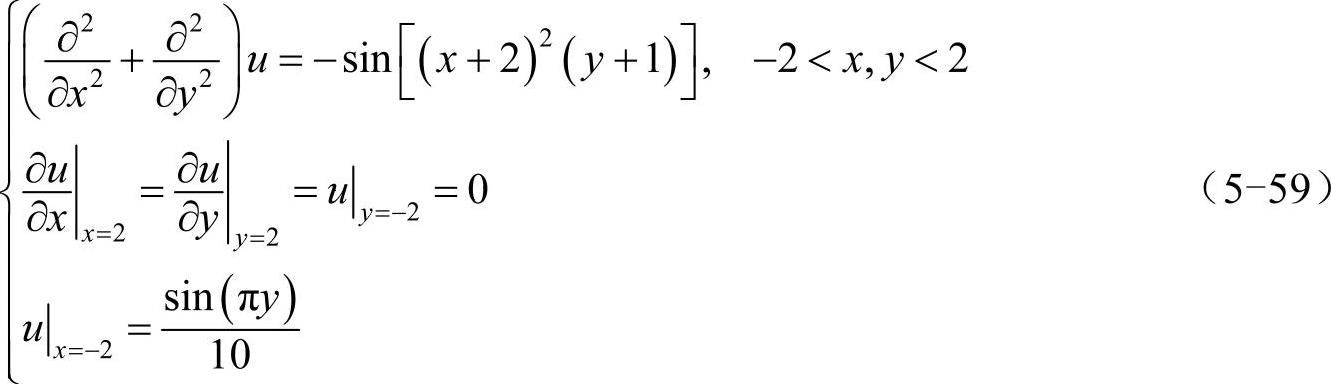
将函数u(x,y)离散化为(N+1)2维向量u：

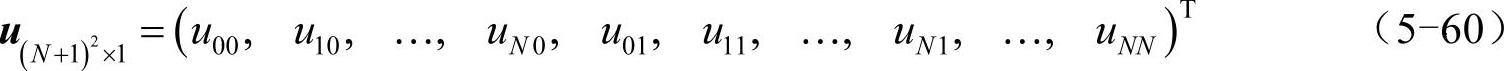
针对在x=-2边界和y=-2边界处的狄利克莱边界条件，可用图5-12所示的方法修改拉普拉斯算符矩阵L（式（5-61））中对应于这两个边界的行。

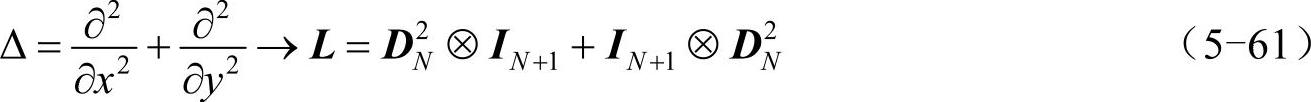
针对在x=2边界和y=2边界处的诺依曼边界条件，需要将5.3.1小节的方法推广到二维空间。先将∂/∂x、∂/∂y写为矩阵形式H_x、H_y：

并把H_x中对应于x=2边界的行覆盖到拉普拉斯算符矩阵L相应的位置，类似地，把H_y中对应于y=2边界的行覆盖到拉普拉斯算符矩阵L相应的位置。在拉普拉斯算符矩阵L上加“-”代表其经过了上述修改，则对于下式：

可知向量f中对应于x=-2边界和y=-2边界的元素，与向量u相应位置的元素相等，向量f中对应于x=2边界和y=2边界的元素，分别与向量H_xu和H_yu在该位置的元素相等。这样，求解式（5-59），只需：(www.xing528.com)

其中，向量f为离散化的f(x,y)=-sin[(x+2)2(y+1)]，它上面的“-”代表对其做如下修改：对应于x=-2边界和y=-2边界的元素分别取sin(πy)/10和0（狄利克莱边界条件），对应于x=2边界和y=2边界的元素取0（诺依曼边界条件）。

具体代码如下：

程序5-18

程序运行结果如图5-22所示。

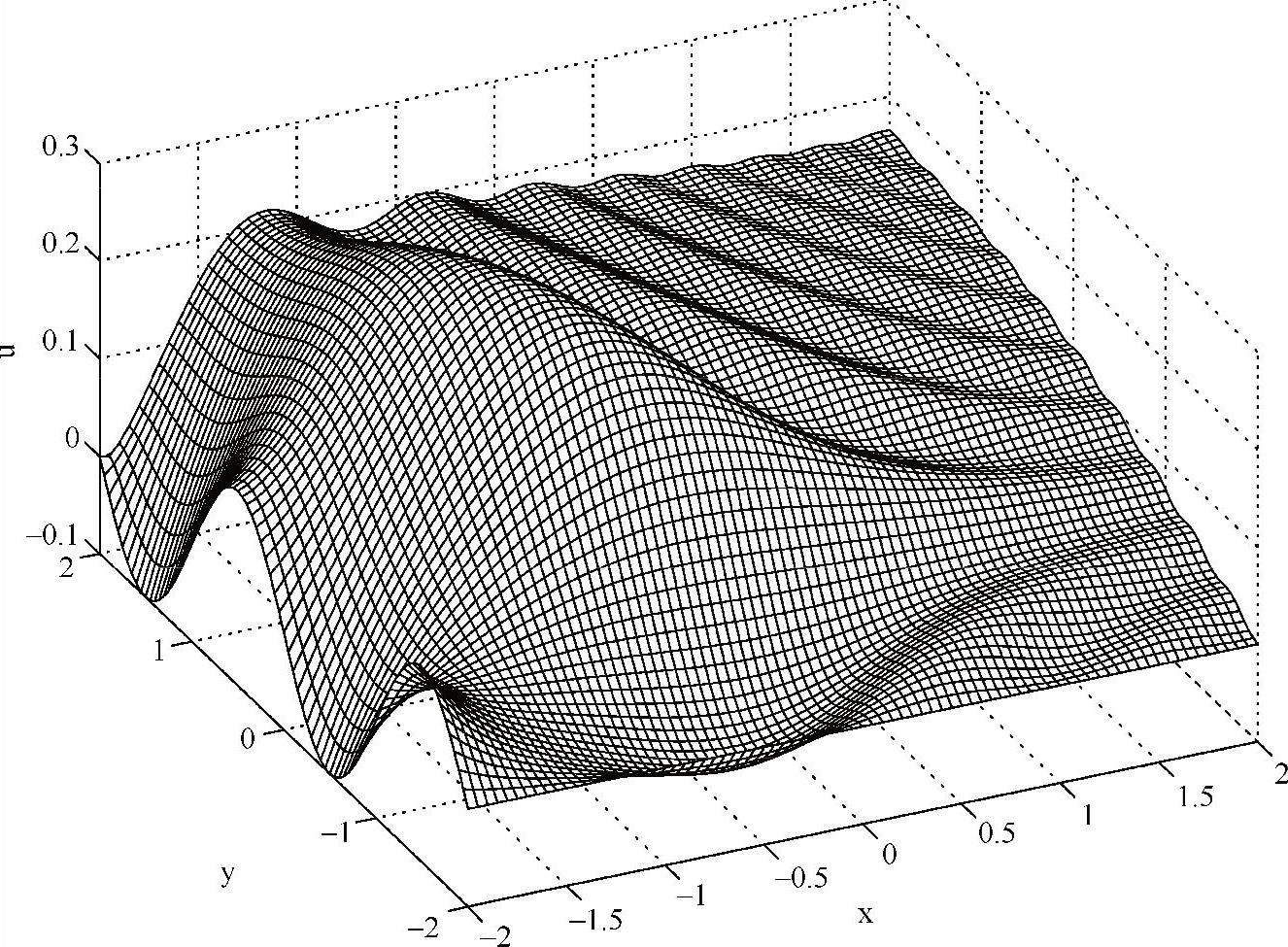
图5-22 二维泊松方程的解