Matlab谱方法高效解一维特征值问题

本小节分析一维无限深方势阱中粒子的波函数分布问题。宽为L的无限深方势阱表达式为：

由于势垒无限高，粒子不能穿过阱壁，所以阱外和阱壁处的波函数必为0。在势阱内，采用自然单位的一维定态薛定谔方程为（取L=2）：

其中，u代表波函数，λ代表能量特征值。上式的精确解为：λ_n=-π²n²/4，u_n=sin[nπ(x+1)/2]，n=1,2,3,…。

用N+1维向量u代表切比雪夫点上的波函数取值，删去其首尾元素得到N-1维向量ũ。则式（5-51）的矩阵形式为：

调用Matlab的eig函数求解矩阵的特征值，代码如下：(www.xing528.com)

程序5-15

这里N=16，所以在每个特征函数上只获得了17个数据点。当特征函数的变化比较剧烈时，这些有限的数据就不足以描绘出特征函数的本来模样。但实际上这些数据点包含了更多的信息，因为本章使用代数多项式作为插值函数，所以利用polyval、polyfit函数（多项式曲线拟合的Matlab函数）可以精确地获取插值函数在其他位置的值，以便画出准确的特征函数图像。如图5-18所示，点为计算结果，曲线为多项式曲线拟合的结果，每幅图上面都标有计算得到的特征值。

需要强调的是，在特征函数的每个周期内，至少有2个数据点才能保证其正确性。比如，对于同样的N，切比雪夫点在原点的密度为等间距点在原点密度的2/π，在d维空间中，这一比例变为(2/π)d。根据式（5-51)的精确解表达式，特征函数的周期为4/n。所以，在原点处，若特征函数每周期内的数据点多于2个，有：2/π·N/2·4/n>2，可化为：n<2N/π≈10。这即是说，当N取16时，计算结果中n≥10的特征值和特征函数都是不足为信的，这与图5-18一致。与精确解相比，第7、8、9个特征值虽有误差，但还比较小，第10、11、12个特征值就很不可信了，特征函数亦如此。

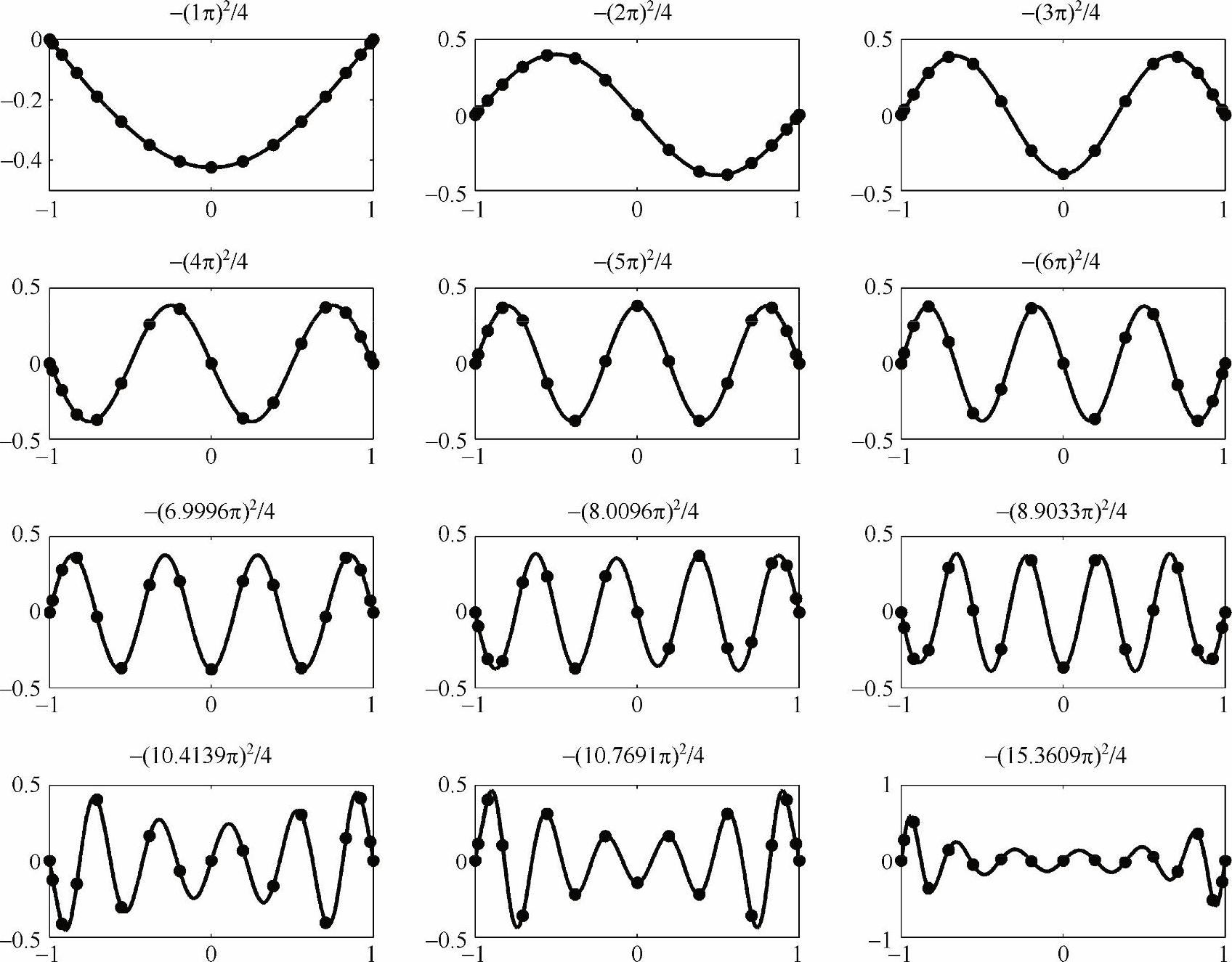
图5-18 一维无限深方势阱中粒子波函数的特征值和特征函数