【摘要】：考虑如下二维热传导方程其中，t代表时间，x、y代表空间坐标，u代表t时刻区域内的温度分布，边界条件给出了边界处的温度。根据式、式处理二维热传导方程等号右边的两项，用ode45计算左边的/t，代码如下：程序5-13主程序代码如下：文件heat.m代码如下：程序的输出结果如图5-16所示，热量迅速地从中央高温区域向四周扩散，温差越小，扩散速度越慢，直到各个位置的温度都趋于0。图5-17 二维热传导方程的计算结果
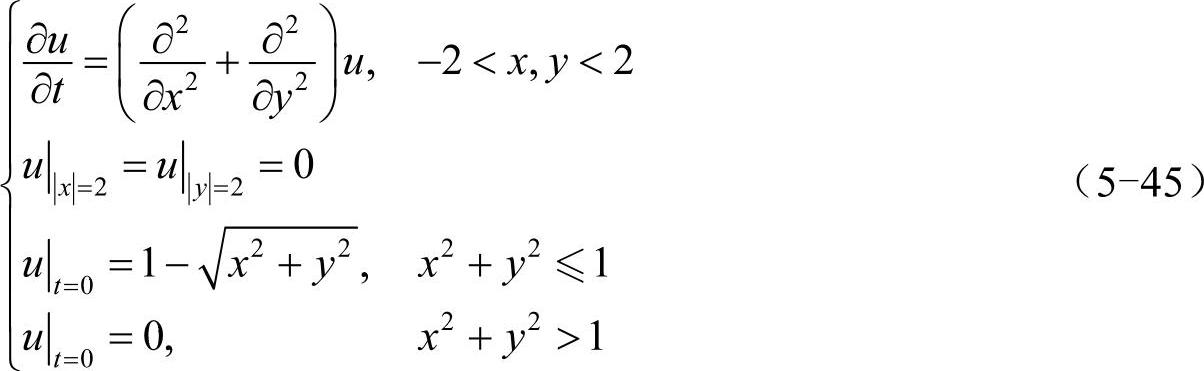
其中，t代表时间，x、y代表空间坐标，u(x,y,t)代表t时刻区域内的温度分布，边界条件给出了边界处的温度。用方阵ũ(N-1)×(N-1)表示除边界以外位置的离散化函数值（定义见式（5-30）），则有：
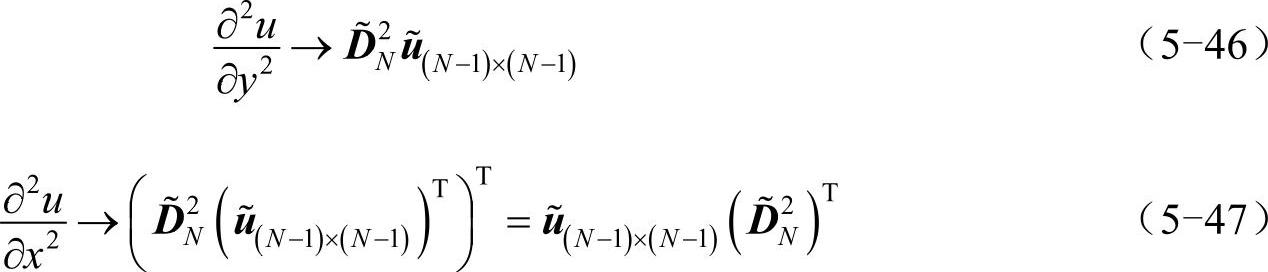
为了避免出现(N-1)2阶大型方阵，所以此处不用式（5-34）的形式表示拉普拉斯算符。只有在迫不得已的情况下才可以使用式（5-34），如：特征值问题、拉普拉斯算符的逆运算等。
根据式（5-46）、式（5-47）处理二维热传导方程等号右边的两项，用ode45计算左边的∂/∂t，代码如下：
程序5-13
主程序代码如下：
文件heat.m代码如下：
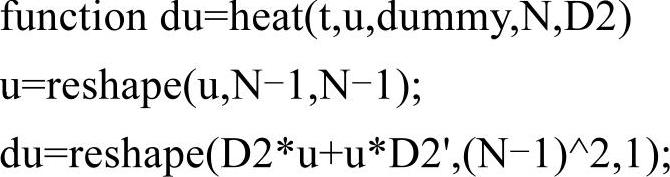
程序的输出结果如图5-16所示，热量迅速地从中央高温区域向四周扩散，温差越小，扩散速度越慢，直到各个位置的温度都趋于0。
下面分析更复杂边界条件下的二维热传导方程：
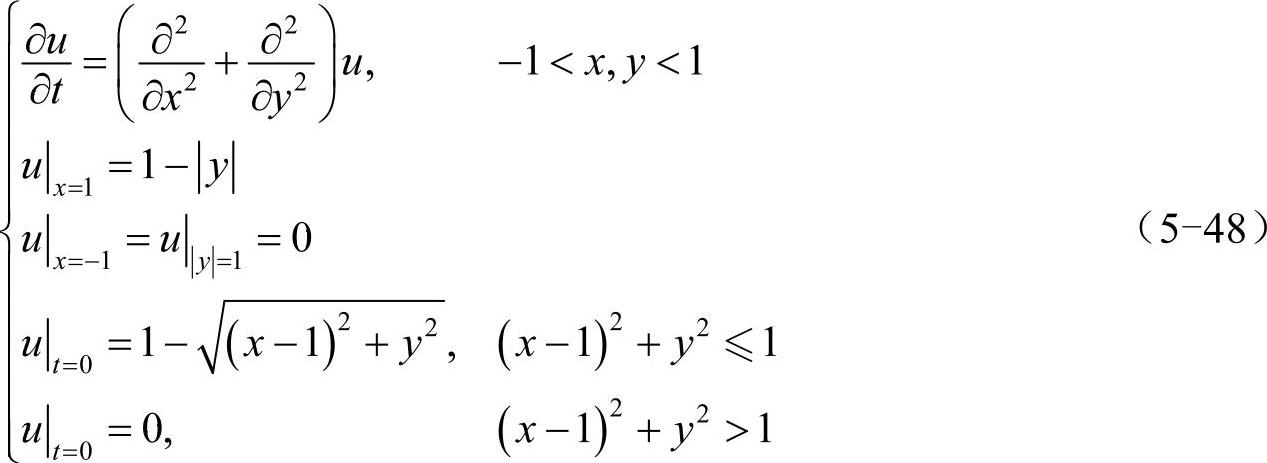(www.xing528.com)
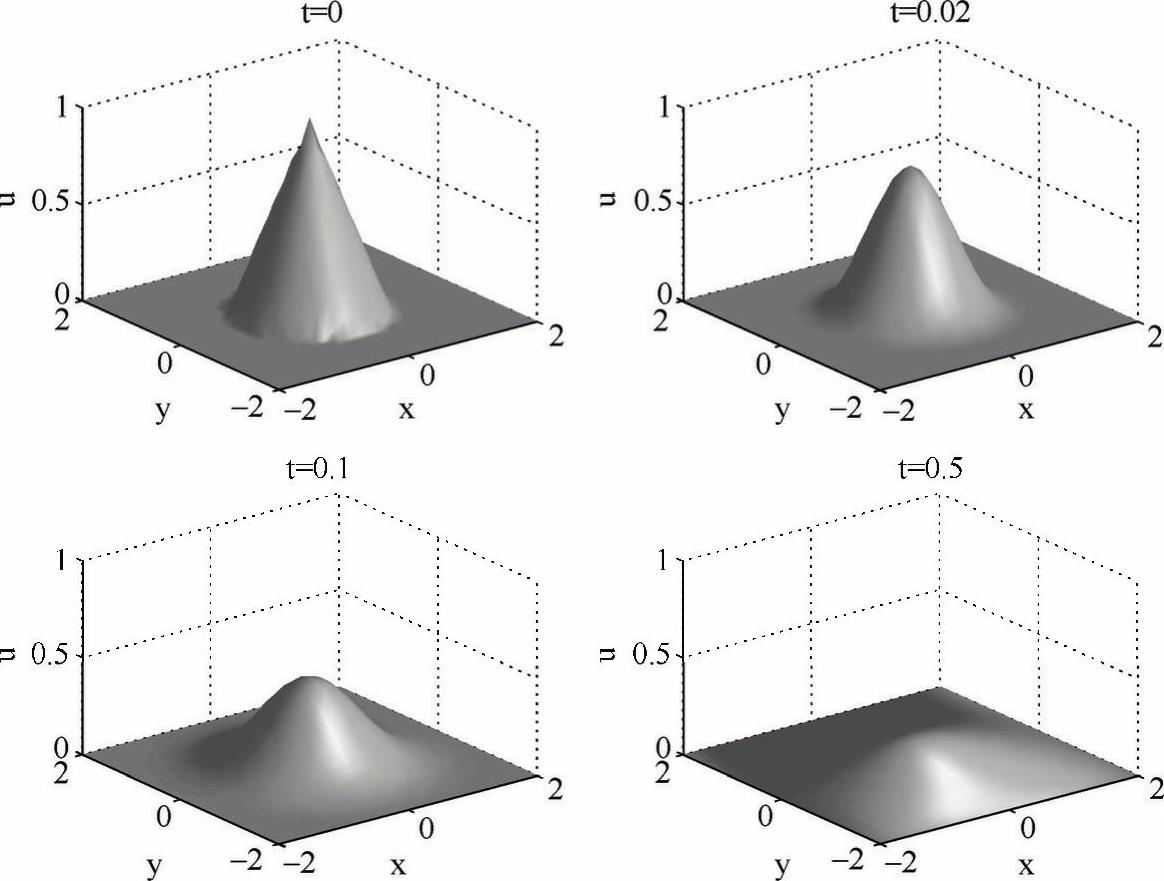
图5-16 二维热传导方程的计算结果
可将其等价写为：
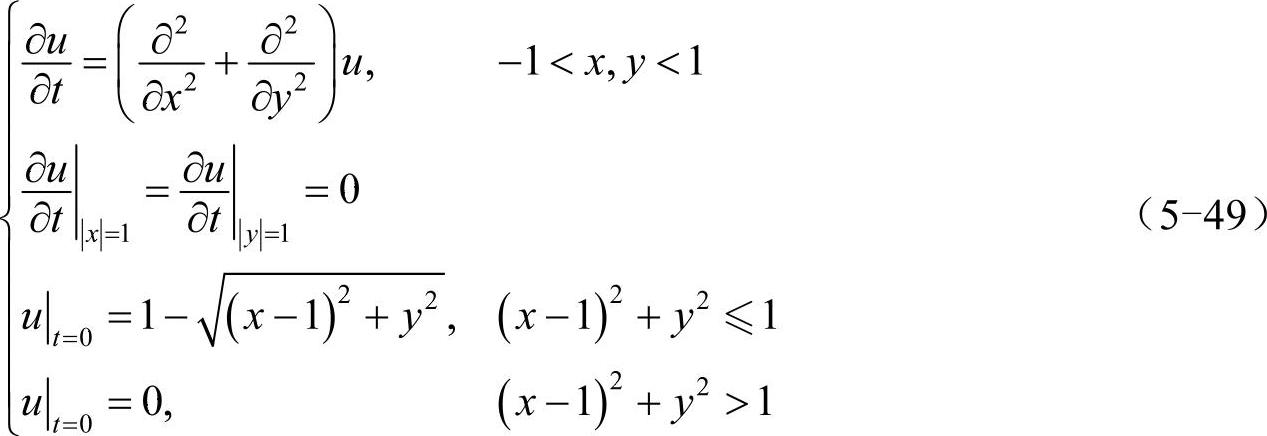
这种形式可直接用ode45函数计算，具体代码如下：
程序5-14
主程序代码如下：
文件heat2.m代码如下：
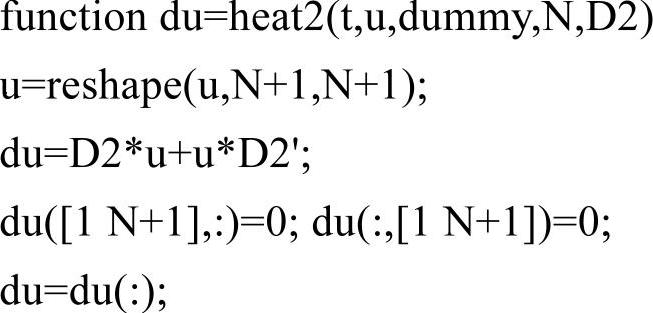
程序输出结果如图5-17所示，从t=0时刻开始，温度分布曲面逐渐趋于光滑，从x=1边界进入的热量被另外三个边界吸收，稳定之后就成了右下图的形态。
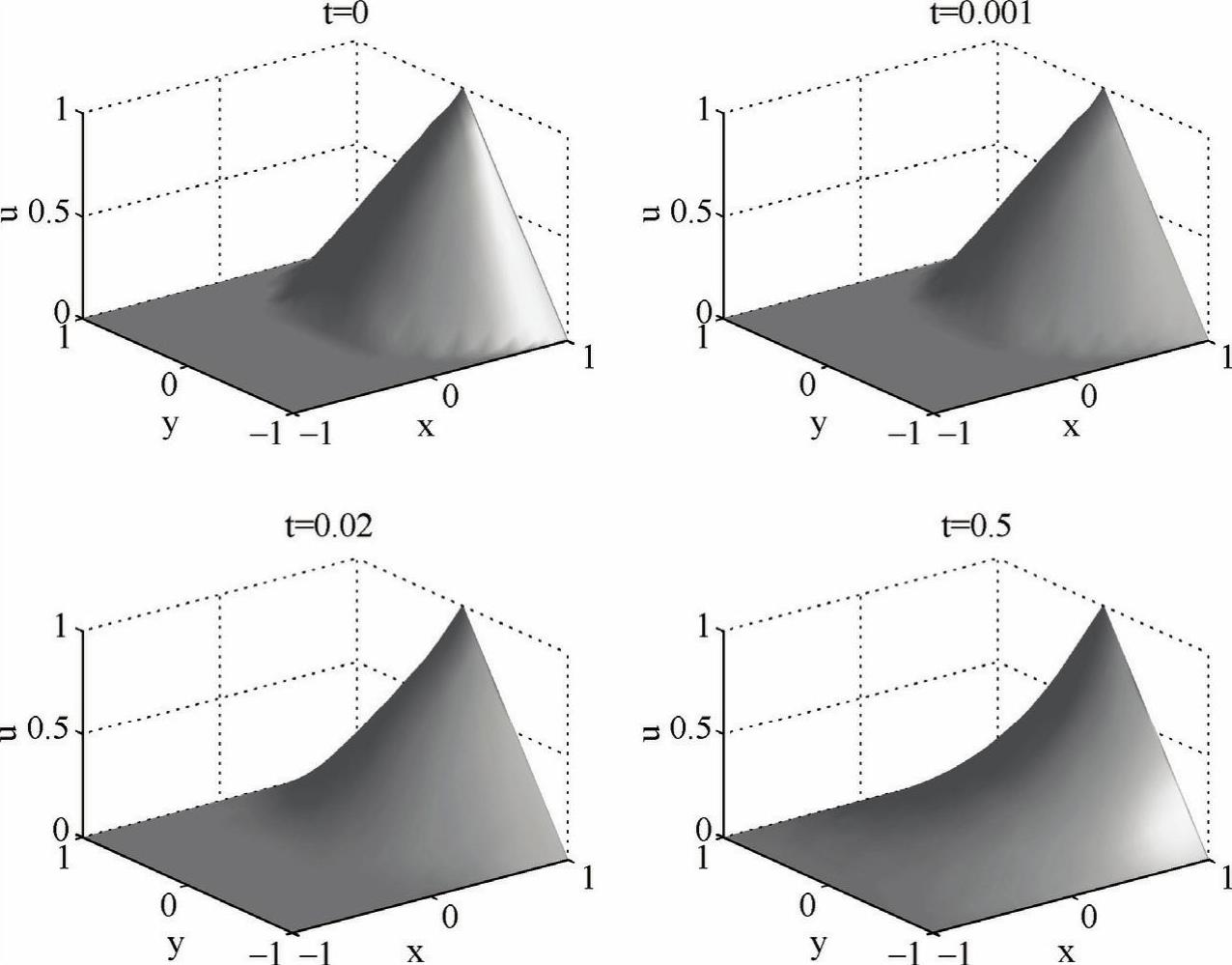
图5-17 二维热传导方程的计算结果
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
