Matlab谱方法高效解Allen-Cahn方程

Allen-Cahn方程的形式为：

离散化x和u(x,t)之后，式（5-41）中的∂²/∂x²可用矩阵D_N²计算，∂/∂t可用ode45函数计算。但需要把边界条件转化为ode45函数能直接处理的形式，所以将上式写为：

容易知道，u(±1,0)=±1及∂u/∂t|_x=±1=0等价于u(±1,t)=±1，所以式（5-41）和式（5-42）是等价的（u(±1,0)=±1是隐含在初始条件里的）。当ε=0.01时，求解式（5-42）的代码如下：

程序5-11

主程序代码如下：

文件allen_cahn.m代码如下：

程序输出结果如图5-14所示，由于计算范围中部的网格比边缘的稀疏，而且切比雪夫求导矩阵的计算精度高，无需较大N值，所以曲面在u变化快的地方就不够光滑（上图）。用interp2函数插值得到的密集、均匀网格上的结果更准确、美观（下图）。

若Allen-Cahn方程的边界条件包含时间t，比如：

(www.xing528.com)

类似地，可将其写为ode45函数能直接求解的等价形式：

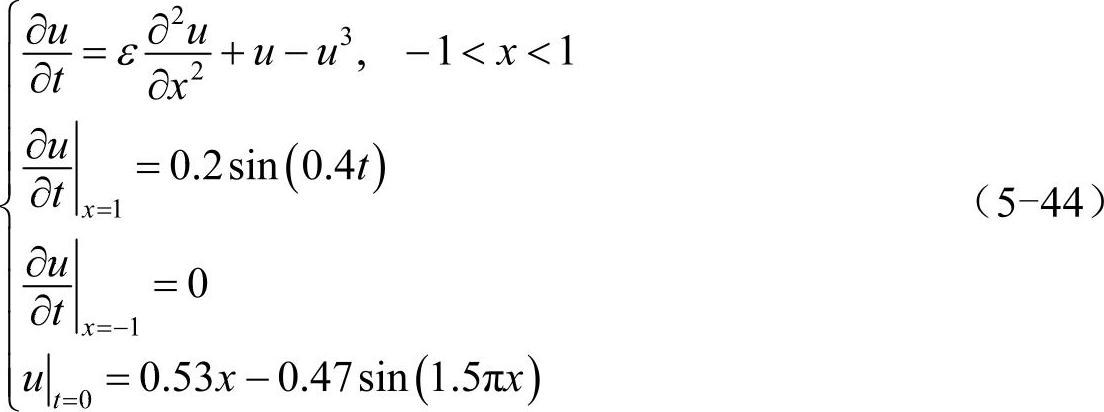
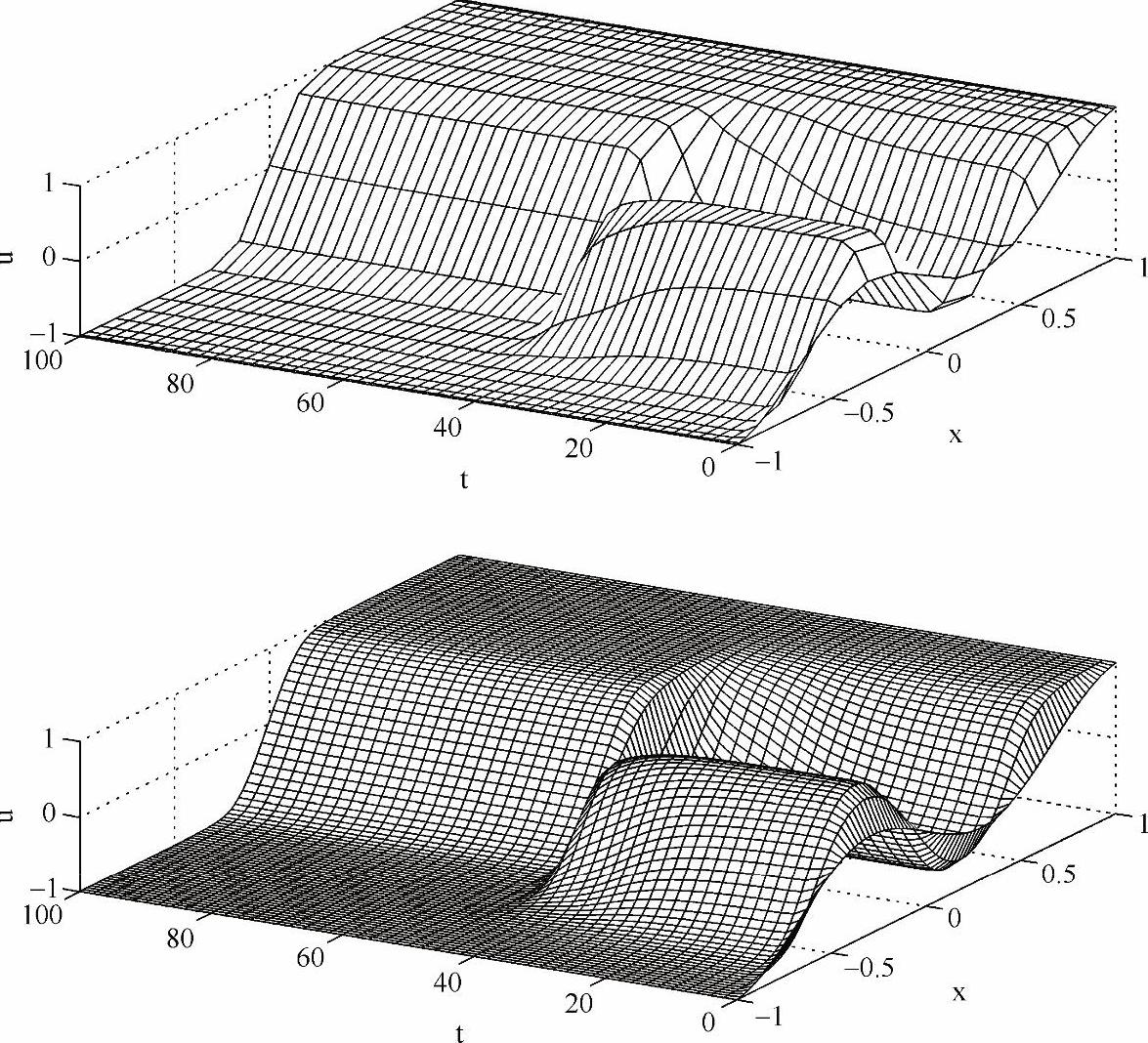
图5-14 上图：计算Allen-Cahn方程的结果；下图：利用interp2插值并 加密、均匀化网格之后的结果

只需对程序5-11中的allen_cahn.m文件稍加改动就能实现式（5-44）的求解，代码如下：

程序5-12

文件allen_cahn.m代码如下：

程序输出结果如图5-15所示。本例和上例的问题均来源于文献[2]，得到的结果与文献[2]完全相同，但这里给出的方法更简洁、精确，有兴趣的读者可以比较一下。

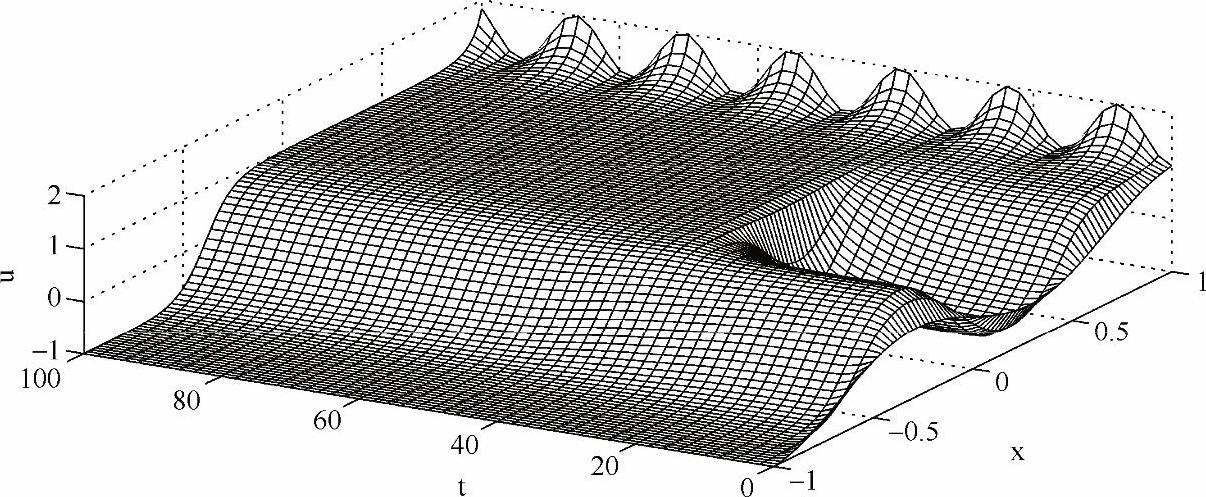
图5-15 Allen-Cahn方程的数值结果