Matlab谱方法解二维泊松方程

对于含有边界条件的二维泊松方程（5-29），不能直接使用式（5-21）和式（5-22）求解，还需要根据边界条件对矩阵和向量进行相应修改。

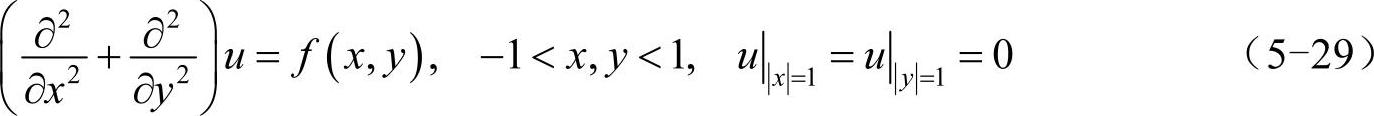
考虑到函数u在边界上的取值为0，所以将图5-6的思路推广到二维平面上来。用N-1阶方阵或(N-1)2维向量ũ表示除边界外所有位置的函数值，即：

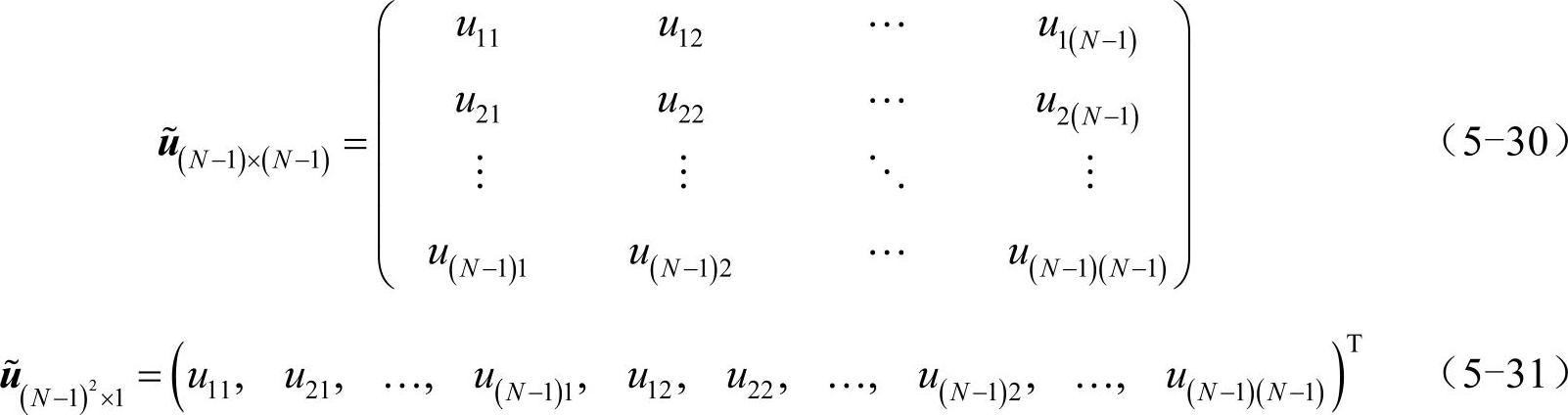
那么，可在u|_|x|=1=u|_|y|=1=0的条件下将式（5-29）中的∂²u/∂y²和∂²u/∂x²写为矩阵形式：

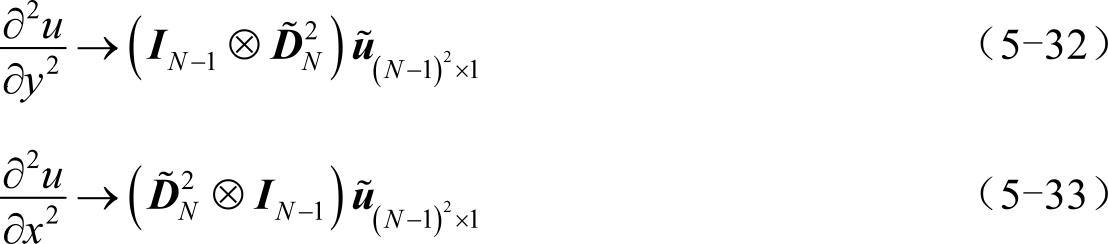
则拉普拉斯算符可写为：

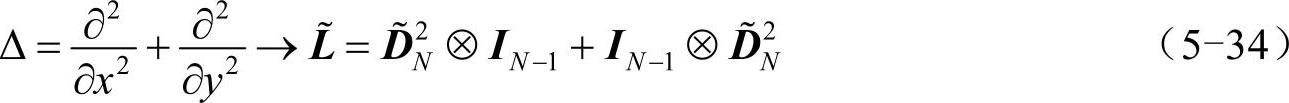
求解式（5-29），只需：

其中，向量f为f(x,y)在各个离散点的取值，上面的“~”代表对其进行删除所有边界值的操作，D_N²上面的“~”代表对其进行删除首尾行、首尾列的操作。在这些过程中，(N+1)2维向量变为(N-1)2维向量，N+1阶方阵变为N-1阶方阵。当然，通过式（5-35）得到ũ之后，还需要在边界对应的位置上补0。

图5-10分别显示了在不考虑边界条件情况下（式（5-21）和式（5-22））和函数在边界取值为0的情况下（式（5-32）和式（5-33）），∂²/∂x²、∂²/∂y²和∂²/∂x²+∂²/∂y²的矩阵形式，每个点表示一个非零元素。N=5时，上三图均为6²阶方阵，下三图均为4²阶方阵。与有限差分法所构造的二维求导矩阵相比，二维切比雪夫求导矩阵要更稠密。此外，较之前者，后者的精度更高，所以只需较小的N就可以计算出令人满意的结果，大大地减小了运算量。代码如下：

程序5-7

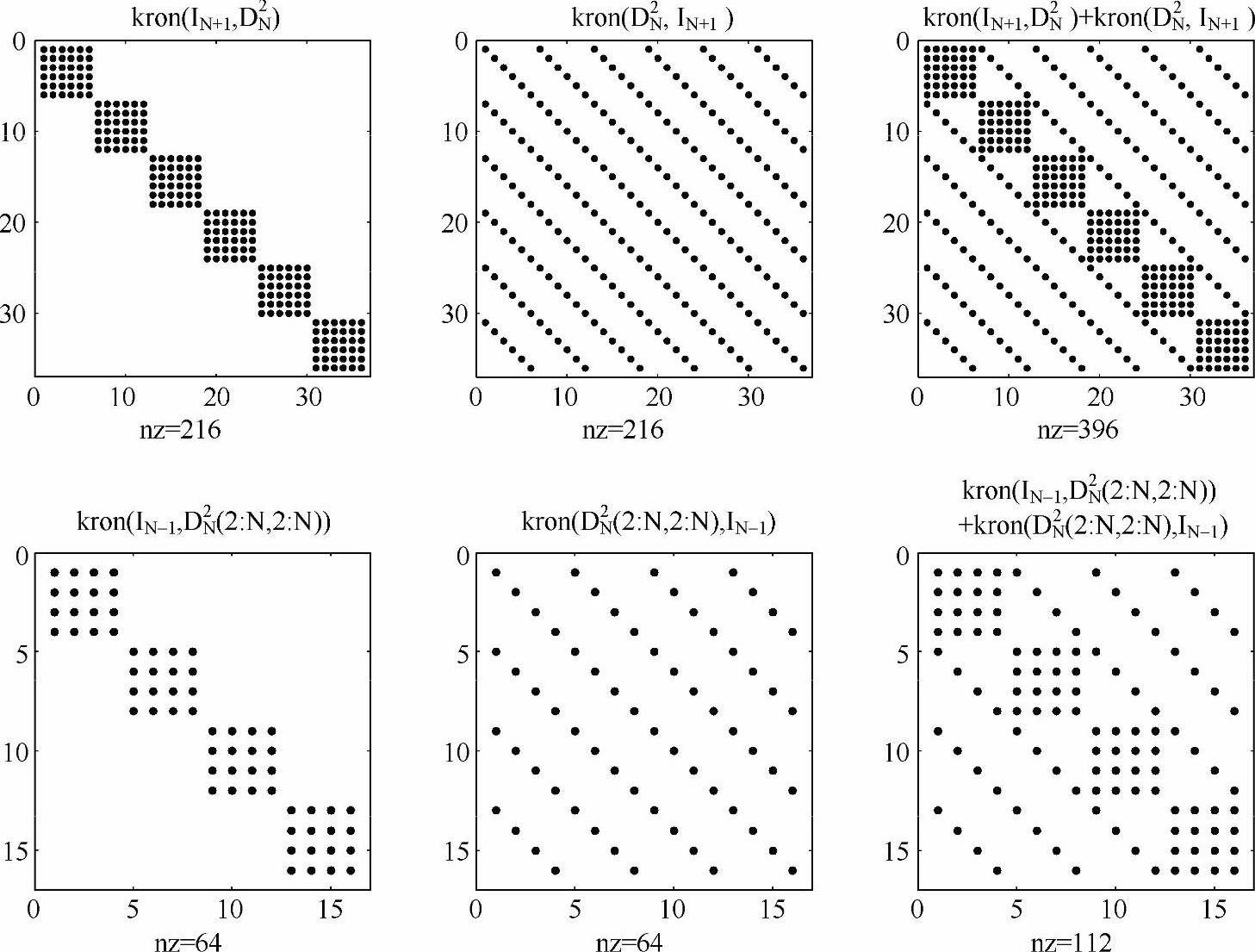
图5-10 不考虑边界条件（上三图）和函数在边界上取值为0（下三图）时， ∂²/∂x²、∂²/∂y²以及∂²/∂x²+∂²/∂y²的矩阵形式，N=5

接下来以二维泊松方程（5-36）为例给出具体求解过程，代码如下：

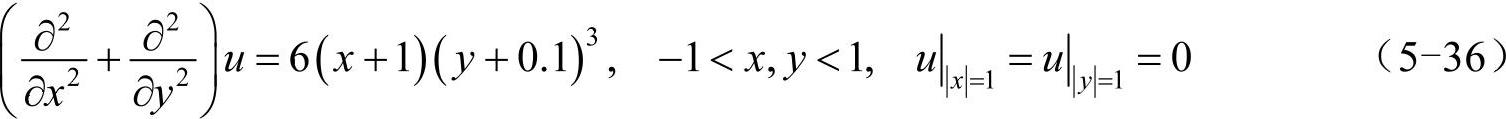
程序5-8

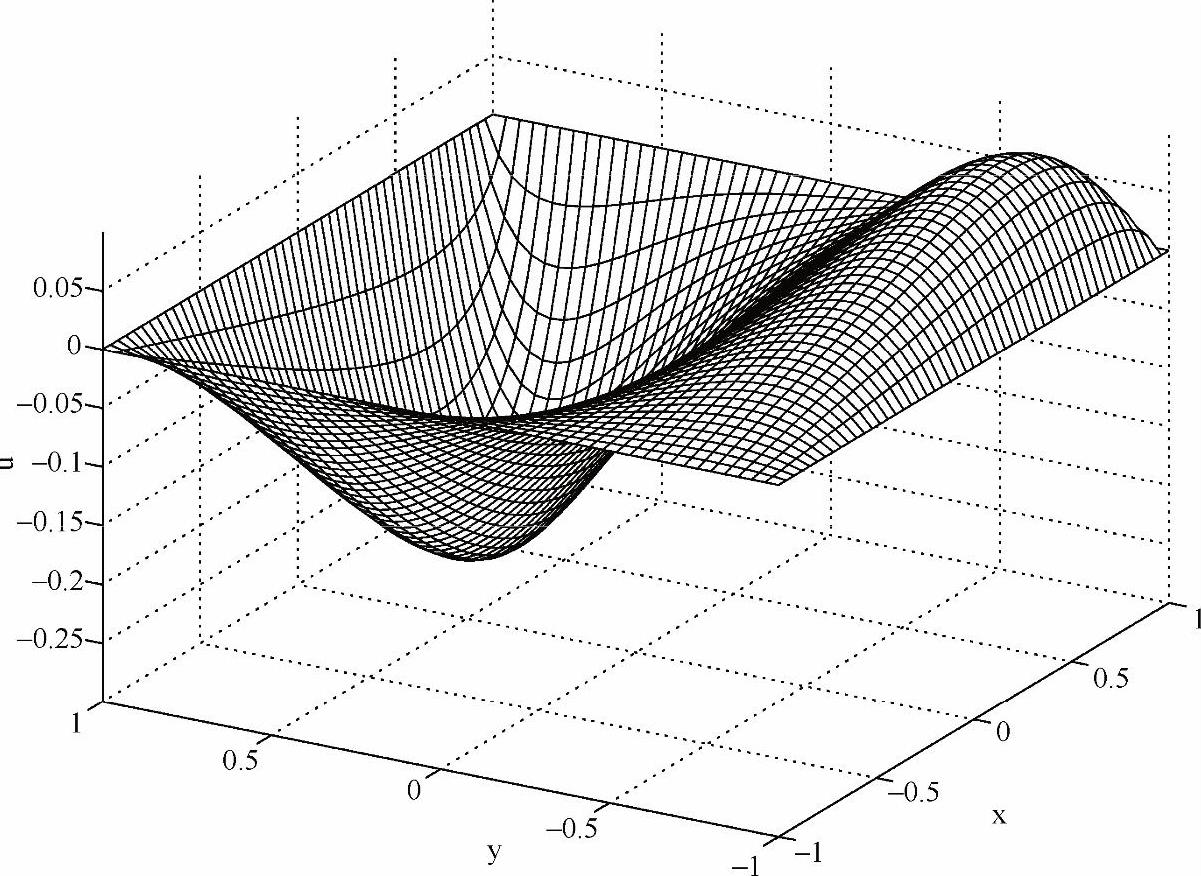
因为N仅为20，且原点附近的网格比较稀疏，所以直接画出来的解的曲面将不够光滑。为解决这一问题，本程序使用了二维数据内插值函数interp2，使最终结果建立在稠密、均匀的网格上，如图5-11所示。

(www.xing528.com)

图5-11 二维泊松方程的解

再来考虑具有更复杂边界条件的二维泊松方程，如式（5-37）所示（其中的sinc(x)函数定义为sin(πx)/πx）：

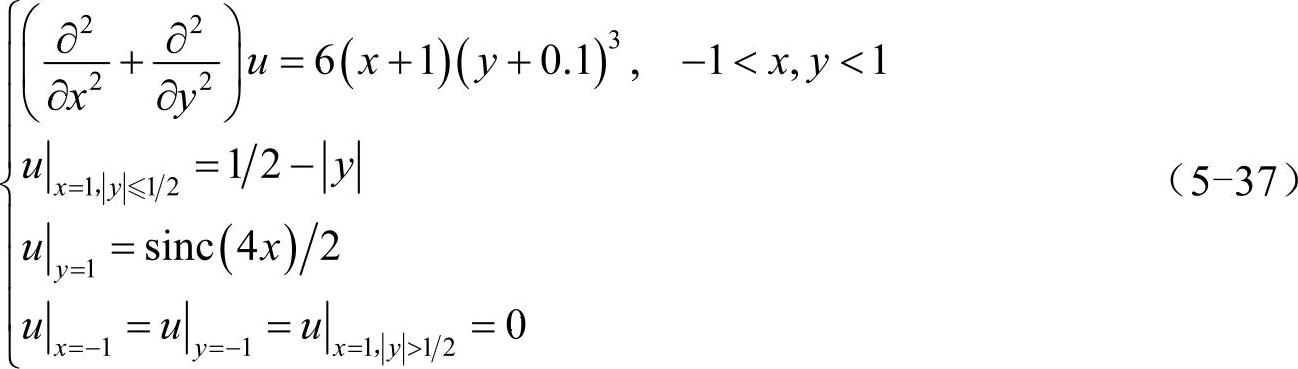
针对这种更具一般性的二维边界条件，可将图5-8所示的思路推广到二维空间上来，先写出不含边界条件的拉普拉斯算符的矩阵形式（注意与式（5-34）区别）：

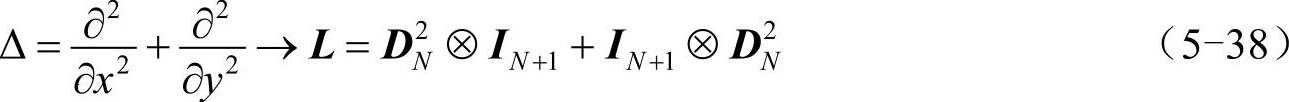
然后对矩阵L进行修改，代码如下：

程序5-9

其中，语句“bound=find(abs(X)==L/2|abs(Y)==L/2);”表示：找到矩阵L中所有对应于边界的行的序号，之后将这些行的所有元素替换为0，最后把这些行中第i个元素设置为1（i是该行的序号）。程序输出的结果显示了这一过程，如图5-12所示。

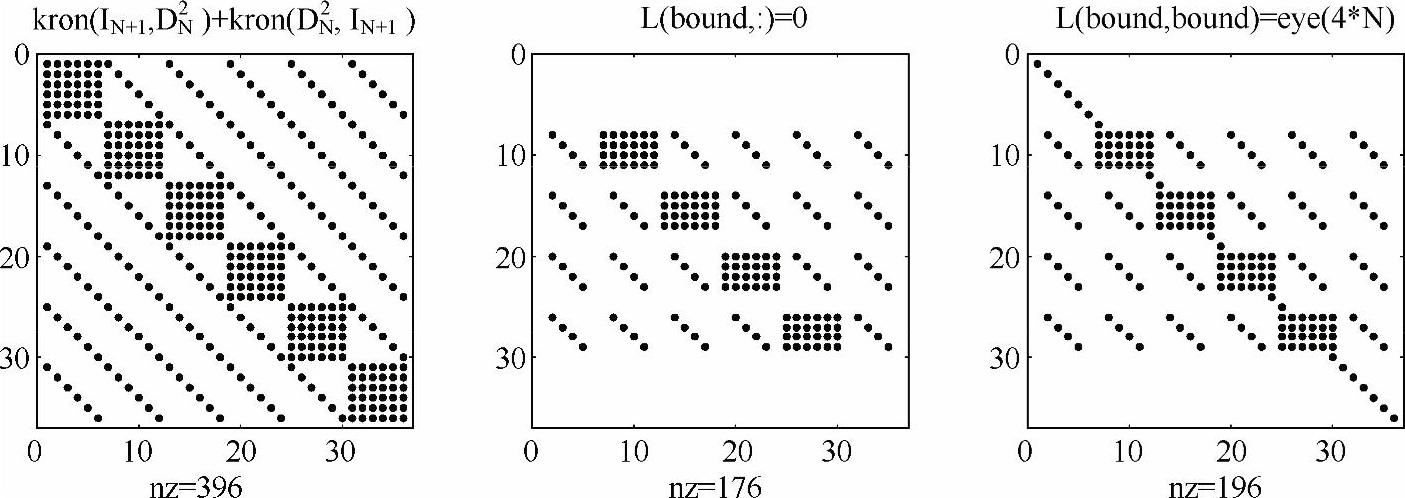
图5-12 修改拉普拉斯算符矩阵的过程

在L上加“^”表示修改后的拉普拉斯算符矩阵。对于式（5-39），容易知道：在边界处，向量f的元素和向量u的元素相等；在其他位置，向量f的元素等于∂²u/∂x²+∂²u/∂y²在该处的值。

类似于式（5-28），求解式（5-37）只需：

其中，f上的“^”表示：在边界处，f的取值与u(x,y)的边界条件一样，而在其他位置的取值为f(x,y)=6(x+1)(y+0.1)3。具体代码如下：

程序5-10

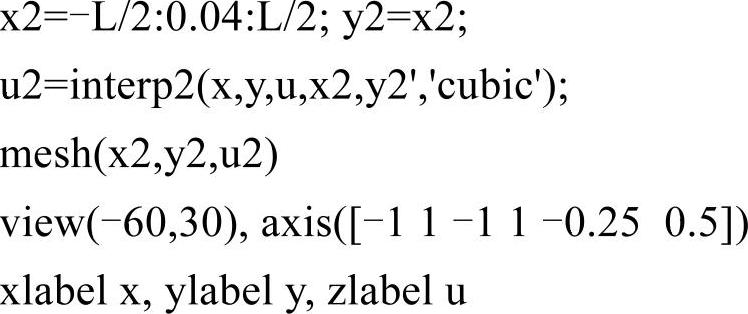
程序输出结果如图5-13所示：

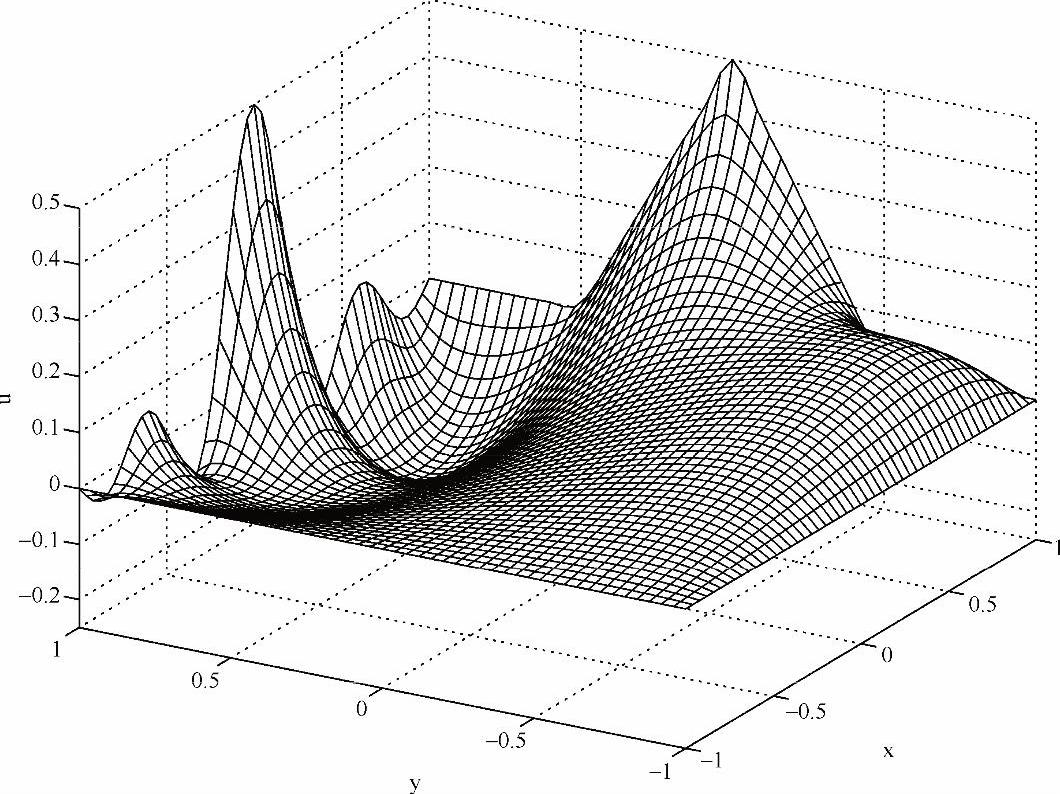
图5-13 复杂边界条件下二维泊松方程的解