Matlab微分方程高效解法：吉布斯和龙格现象解析

首先，比较以下3种对有限区间内非周期函数插值的方法：

（1）用第4章的方法在周期性边界条件下对函数进行插值。

（2）在区间内等间距的点上对函数进行代数多项式插值。

（3）在区间内的切比雪夫点（Chebyshev points）上对函数进行代数多项式插值。

方法1采用了周期性边界条件，如果该函数在计算区间的边界附近迅速衰减到0或趋于某一特定值，那么就可以在周期性边界条件下对其精确插值（前面章节有这样的实例）。但一般来讲，方法1相当于将该函数强制转化为在边界处间断、周期为L的周期函数（L为区间宽度），且认为其插值函数的形式是周期sinc函数的线性叠加。如此得到的插值函数会在间断点附近产生震荡，带来误差。若增加插值所使用的离散点个数N，震荡将向间断点处靠近，且震荡幅度趋于一个常数，约等于间断点处跳变值的9%，这种现象称为吉布斯现象（Gibbs phenomenon）。

例如：对定义在[-π,π]上的y=e^x函数进行扩展，得到在边界处间断、周期为2π的周期函数，此周期函数的插值函数为：

其中，x_j为区间[-π,π]上间隔2π/N的N个点（即：-π,-π+2π/N,-π+4π/N,…,π-2π/N），y_j为x_j处的函数值，S_N为周期sinc函数，N取64。如图5-1所示，插值函数p(x)在间断点处出现了振荡，极大地影响了插值精确度。实现上述过程的代码如下：

程序5-1

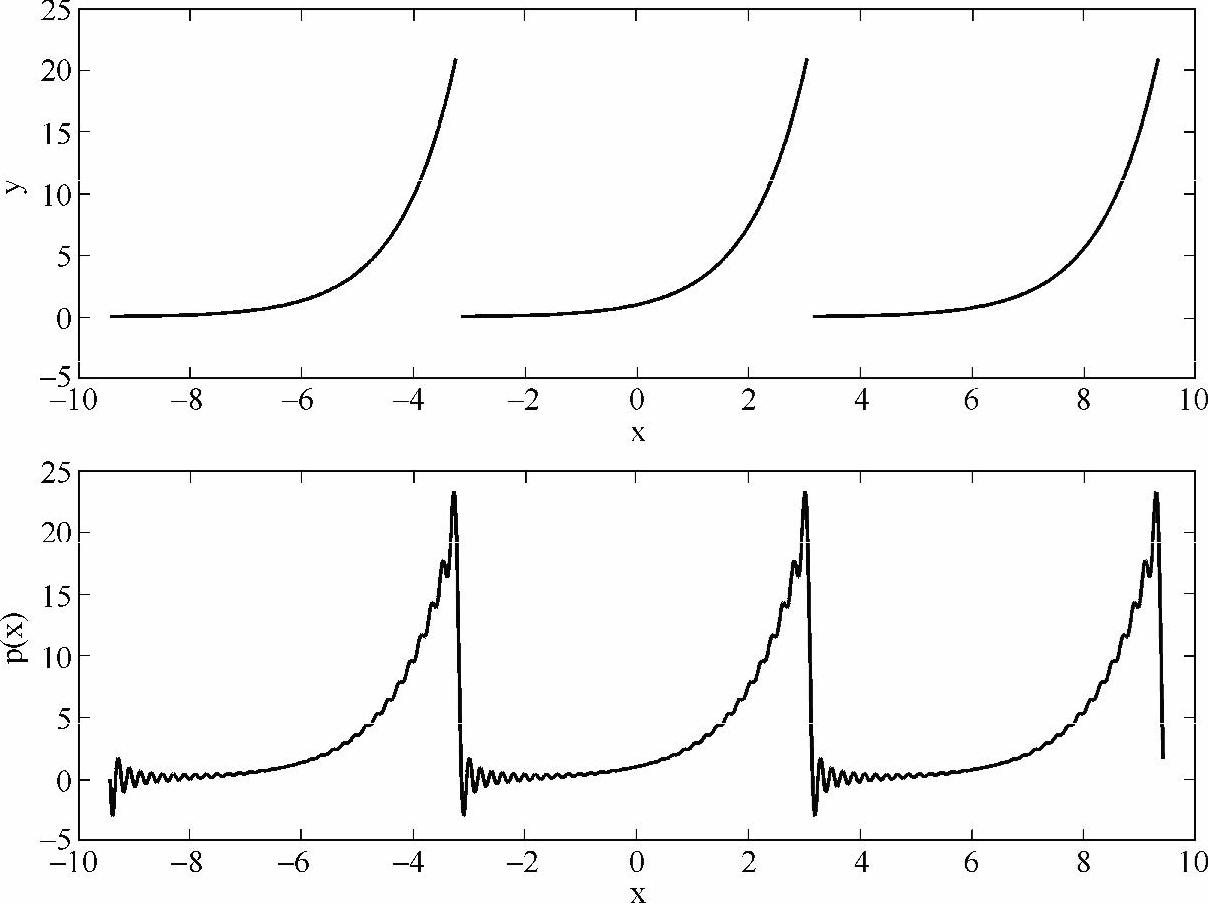
图5-1 上图：由[-π,π]上的y=e^x函数扩展得到的在边界处间断、周期为2π的周期函数； 下图：插值函数出现了吉布斯现象

方法2是一种比较容易想到的方法：在宽为L的区间内均匀地选取N+1个位置（即：-L/2,-L/2+L/N,-L/2+2L/N,…,L/2-2L/N,L/2-L/N,L/2），用N次代数多项式在这些位置对函数进行插值，插值函数的形式为：

p(x)=a₀+a₁x+…+a_Nx^N （5-2）

此方法没有使用周期性边界条件，避免了吉布斯现象的出现。但是，N次代数多项式必然存在N-1个极值，它将导致插值函数p(x)在区间的边界处出现震荡，并随着N的增大而变得更加严重，这被称为龙格现象（Runge's phenomenon）。由于震荡带来误差，所以方法2也是行不通的，后面会用实例说明。

方法3在区间内选取了不均匀的N+1个位置——切比雪夫点，在区间[-1,1]内的切比雪夫点的位置为：(www.xing528.com)

x_j=cos(jπN),j=0,1,…,N （5-3）

可以把这些切比雪夫点理解为上半个单位圆上等间距的点在横轴的投影，N=8和N=16的情况如图5-2所示。注意切比雪夫点是从右向左排序的。

图5-2 切比雪夫点是上半个单位圆上等间距的点在横轴的投影。左图：N=8，右图：N=16

下面这个例子使用方法2和方法3对函数y=1/(1+25x²)进行代数多项式插值，并比较了插值函数，代码如下：

程序5-2

程序输出结果如图5-3所示，在均匀点上对函数进行代数多项式插值会导致在区间边界附近出现很大误差，而在切比雪夫点上对函数进行代数多项式插值则几乎没有这个问题。随着N的增大，前者的误差会越来越大，而后者的误差约正比于2^-N。

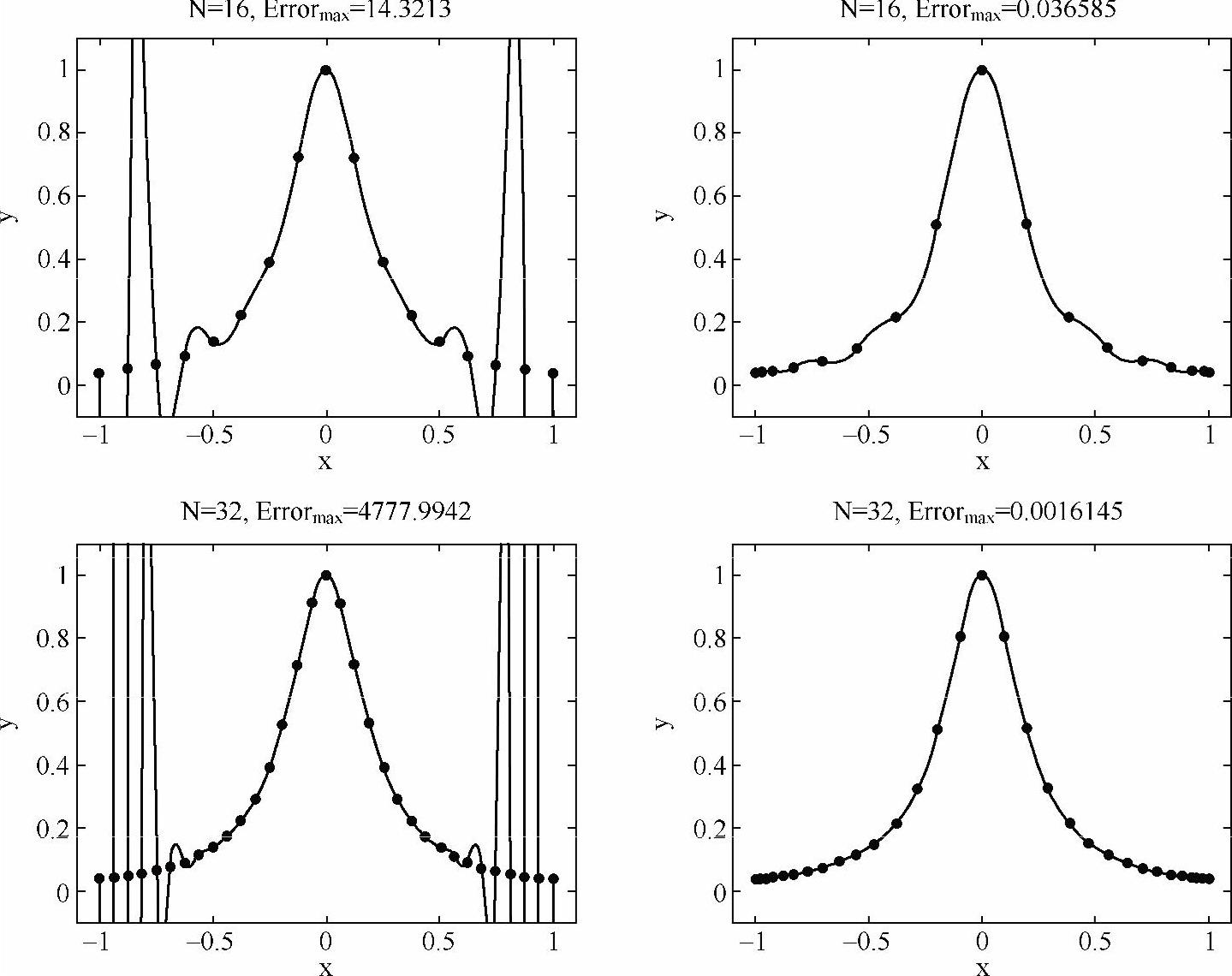
图5-3 根据离散数据（点）得到插值函数（曲线）。左边两图：使用均匀点插值； 右边两图：使用切比雪夫点插值

通过上面的分析可知，由于方法3没有使用周期性边界条件，不存在间断点，从而杜绝了吉布斯现象，同时又通过切比雪夫点划分区间，避免了龙格现象，是一种针对有限区间内非周期函数的理想插值方法。

实际上，为了消除龙格现象，有很多非均匀划分区间的方法，使用切比雪夫点划分的方法只是其中之一。这些方法都符合以下条件：当N→∞时，点的密度分布满足

证明从略。