Matlab微分方程高效解法：二维平流-扩散方程求解

二维平流-扩散方程（advection-diffusion equation）描述了大气的准二维运动，它的形式如下：

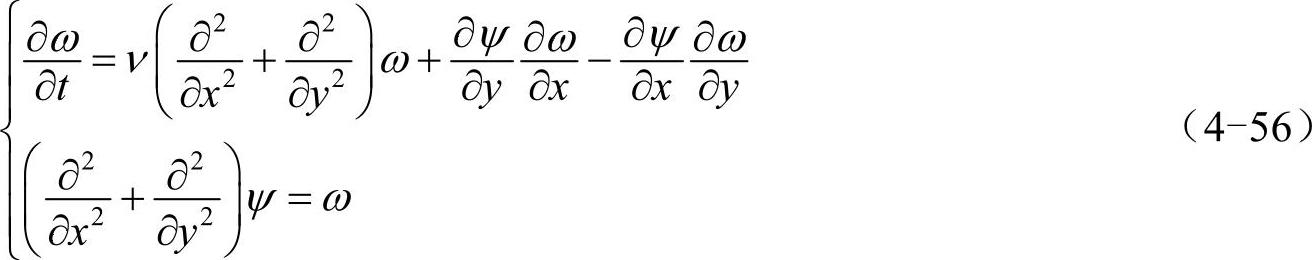
其中，ψ、ω分别为流函数（stream function）和涡量（vorticity），x、y为空间坐标，t为时间，v为一常数。式（4-56）中的第一式同时包含了平流部分——∂ψ/∂y·∂ω/∂x-∂ψ/∂x·∂ω/∂y，以及扩散部分——ν(∂²/∂x²+∂²/∂y²)ω。将ψ和ω离散化为方阵ψN×N和ω_N×N之后，等号右边可写为ν[ω_N×N(D_N(2))T+D_N(2) ω_N×N]+D_NψN×N·ω_N×N(D_N)T-ψN×N(D_N)T·D_NωN×N，等号左边的∂/∂t使用ode45函数计算。

流函数ψ可看作涡量ω的一个参量，计算涡量ω的过程中需要先用式（4-56）中的第二式求解流函数ψ，这是一个对ω的积分运算，由于产生了积分常数c，所以ψ并不是唯一的，即：ψ=ψ0+c。但是注意到式（4-56）中的ψ都是以导数的形式存在，所以积分常数c并不会影响ω的计算结果，可不做考虑。计算流函数ψ有两种方法：

（1）直接对∂²/∂x²+∂²/∂y²的矩阵形式求逆得到积分矩阵，对ω进行积分：

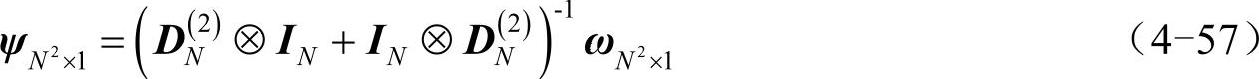
（2）利用第3章的方法，对方程做二维傅里叶变换，将积分运算转化为在频域上的除运算（注意用技巧避免分母为0）：

因为方法一中存在对N²阶方阵的求逆运算，运算量较大，所以这里采用方法二。

使用周期性边界条件，初始条件ω(x,y,0)=sech(x²+y²/20)，取v=0.001，数值计算二维平流-扩散方程的代码如下：

程序4-9(www.xing528.com)

主程序代码如下：

advection_diffusion.m文件代码如下：

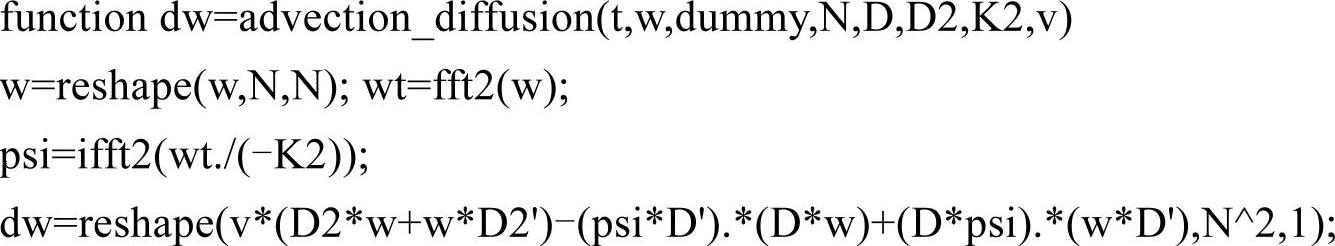
程序输出结果如图4-12所示，随着时间t的推移，涡量ω的分布出现了逆时针的旋转。如果将平流部分变号，旋转方向将变为顺时针，读者可自行尝试。

图4-12 二维平流-扩散方程计算结果

[1]锁模是光学里一种用于产生极短时间激光脉冲的技术。