【摘要】：本小节以反应-扩散系统中的Schnakenberg模型为例介绍计算斑图的方法，它的形式如下：其中，u和v可看做两种化学反应物质的浓度，x、y为空间坐标，t为时间，参数取值如下：a=0.1、b=0.8、d=26、γ=100。等号左边的/t交给ode23函数计算即可，具体代码如下：程序4-8主程序代码如下：schnakenberg.m文件代码如下：程序输出的结果如图4-11所示，t=0时的初始条件设置为噪声，随后图形逐渐开始自组织。图4-11 计算二维Schnakenberg模型得到的斑图
1952年，被称为计算机理论之父的英国科学家图灵提出了一个新颖的想法：一些动物（如：老虎、金钱豹）身上之所以会长着有规律的条纹斑点图案（斑图），是因为在细胞中存在一种化学物质，由于反应-扩散系统的特性而自组织形成了斑图。这种想法逐渐被后来的实验和理论所证实。本小节以反应-扩散系统中的Schnakenberg模型为例介绍计算斑图的方法，它的形式如下：
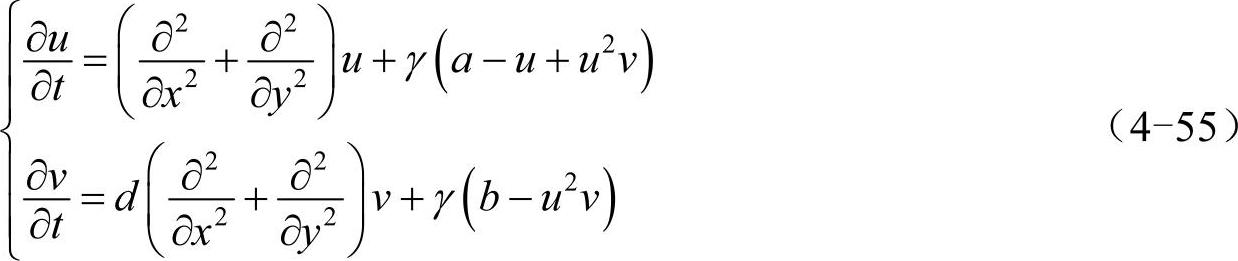
其中，u和v可看做两种化学反应物质的浓度，x、y为空间坐标，t为时间，参数取值如下：a=0.1、b=0.8、d=26、γ=100。由于动物表皮为闭合曲面，因此使用周期性边界条件是合理的。
若把u离散化为方阵uN×N，则方程中的(∂2/∂x2+∂2/∂y2)u可表示为uN×N(DN(2))T+DN(2) uN×N，(∂2/∂x2+∂2/∂y2)v同理。等号左边的∂/∂t交给ode23函数计算即可，具体代码如下：
程序4-8
主程序代码如下：
(www.xing528.com)
schnakenberg.m文件代码如下：
程序输出的结果如图4-11所示，t=0时的初始条件设置为噪声，随后图形逐渐开始自组织。在t=0.3时，斑图已经初具雏形，十分类似动物皮毛上的图案。
图4-11 计算二维Schnakenberg模型得到的斑图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
