高效解法：谱方法求解一维波动方程

对于一根两端固定、细长柔软的弦线，若其平衡位置为x轴，u(x,t)表示弦上坐标为x的点在时刻t垂直于x方向的位移，则弦的自由振动方程为：

实际上，杆的纵振动方程、理想传输线的电报方程也是此方程。对于无界（-∞＜x＜∞）弦的自由振动，如果计算区间足够大，那么就可以采用周期性边界条件。这里取a=1，初始条件为：

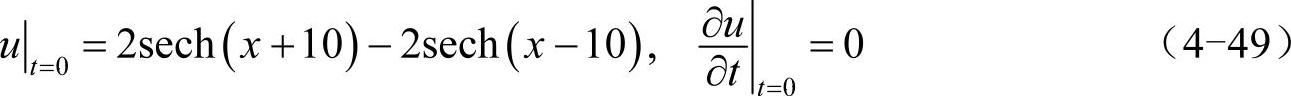
在数学物理方法中，给定初始条件的无界弦自由振动方程存在解析解，称为达朗贝尔公式。对于初始条件（4-49），弦各处的初始速度为0，弦的初始波形包含了x=±10处的2个sech函数。根据达朗贝尔公式，这2个sech函数将分别分裂成两半，以速度a沿着x轴的正方向和负方向传播，即正行波和反行波，这些正行波和反行波的叠加就给出了弦的总位移。下面给出数值解法的代码，并与达朗贝尔公式的预测进行比较。

程序4-4

主程序代码如下：(www.xing528.com)

wave1D.m文件代码如下：

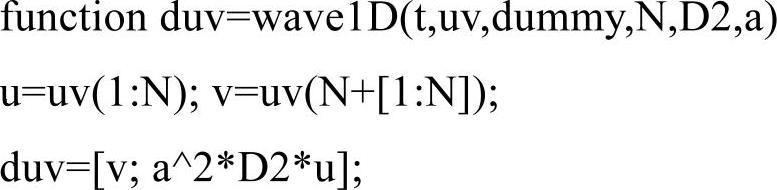
程序输出结果如图4-7所示，上图是弦在t=0,5,10,20时的位移u，下图是位移u随位置x、时间t的变化情况。初始条件中的sech函数在t=0之后分裂为正行波和反行波，正行波和反行波的振幅为分裂前sech函数振幅的一半，并分别以速度a=1向两边传播。在t=10时，其中的一对正行波和反行波叠加为0，所以它们暂时消失了。总之，数值计算的结果与达朗贝尔公式的预测完全一致。

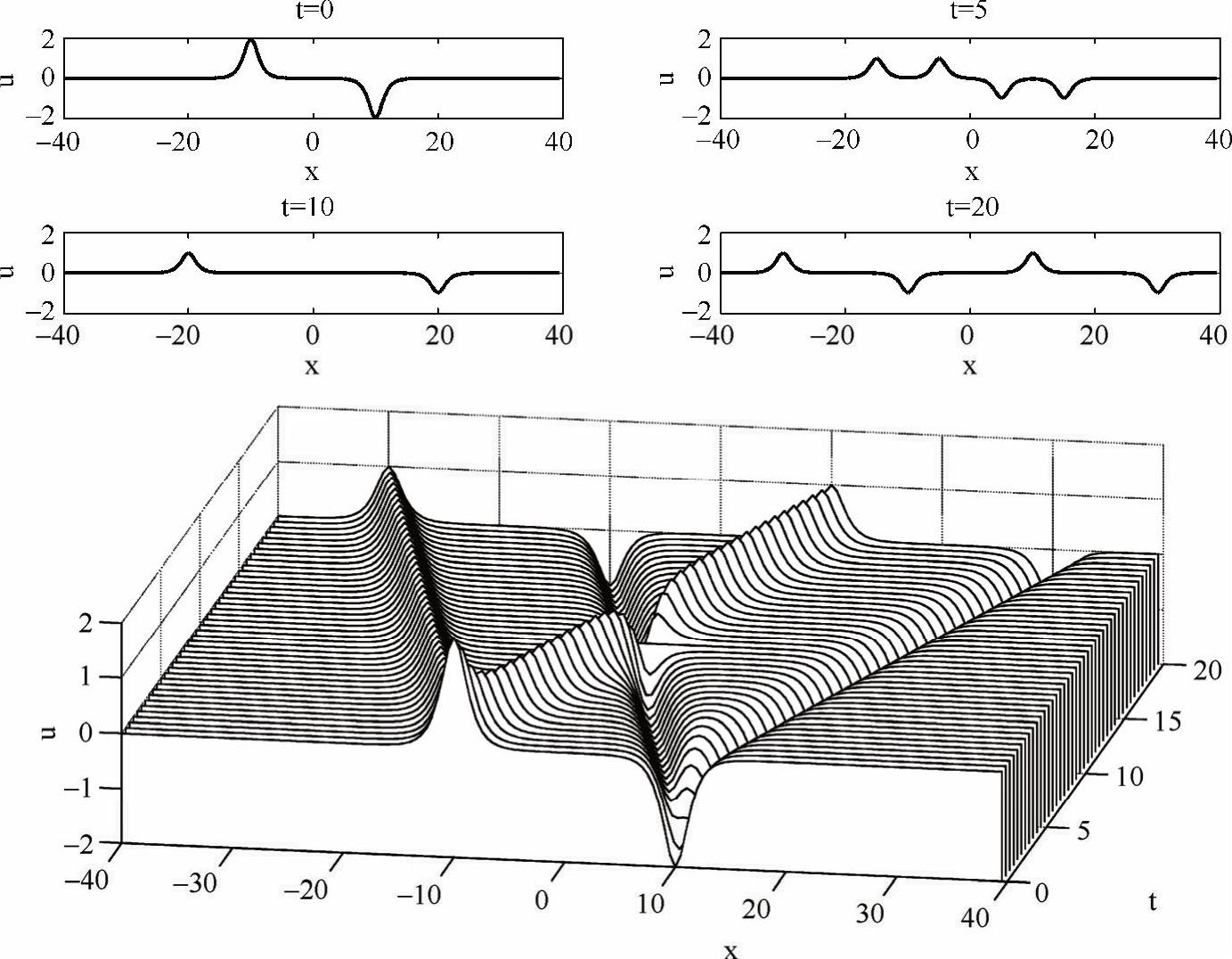
图4-7 一维波动方程数值解