谱方法解一维线性谐振子定态薛定谔方程

一维谐振子的特征值问题是量子力学中一个重要的基本问题，分子的振动、晶格的振动、原子核表面的振动和辐射场的振动等都可以分解为若干彼此独立的一维谐振动。若选取自然平衡位置为坐标x的原点和势能零点，则一维线性谐振子的势能可以表示为U(x)=Kx²/2，其中K是描述简谐作用力强度的参数。采用自然单位，一维线性谐振子的特征值问题有如下形式：

其中，u为波函数，λ为特征值，且u≠0。此问题存在解析解，特征值λ_n=2n+1，其中n=0,1,2,…，相应的特征函数为：

其中，H_n(x)为埃尔米特多项式（Hermite polynomials）。由于特征函数随着|x|的增加而迅速衰减，所以，若计算区间足够宽的话，就能保证特征函数在边界处的值总是近似为0，这样即使用周期性边界条件来处理此特征值问题也无妨。或者，也可以认为这里的势场是周期势场。

将x和u离散化为：x=(x₁,x₂,…,x_N)^T，u=(u1,u2,…,uN)^T，那么式（4-41）可写为矩阵形式：

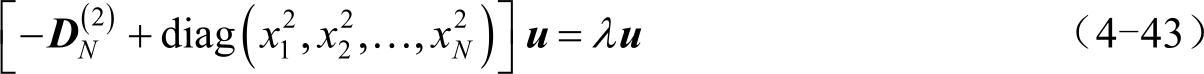
用Matlab中的eig函数可方便地求解这种矩阵形式的特征值问题，具体代码如下：(www.xing528.com)

程序4-2

结果如图4-4所示，前25个特征值、特征函数与解析解基本一致。随着特征值的增加，特征函数的分布范围也越来越大。如果特征函数的分布范围超出了计算区间，那么周期性边界条件会导致错误，所以一定要保证计算区间足够大。注意，每个特征值对应的特征函数并不是唯一的，如果u_n是特征值为λ_n的特征函数，那么ku_n也必是它的特征函数，k为非零常数。

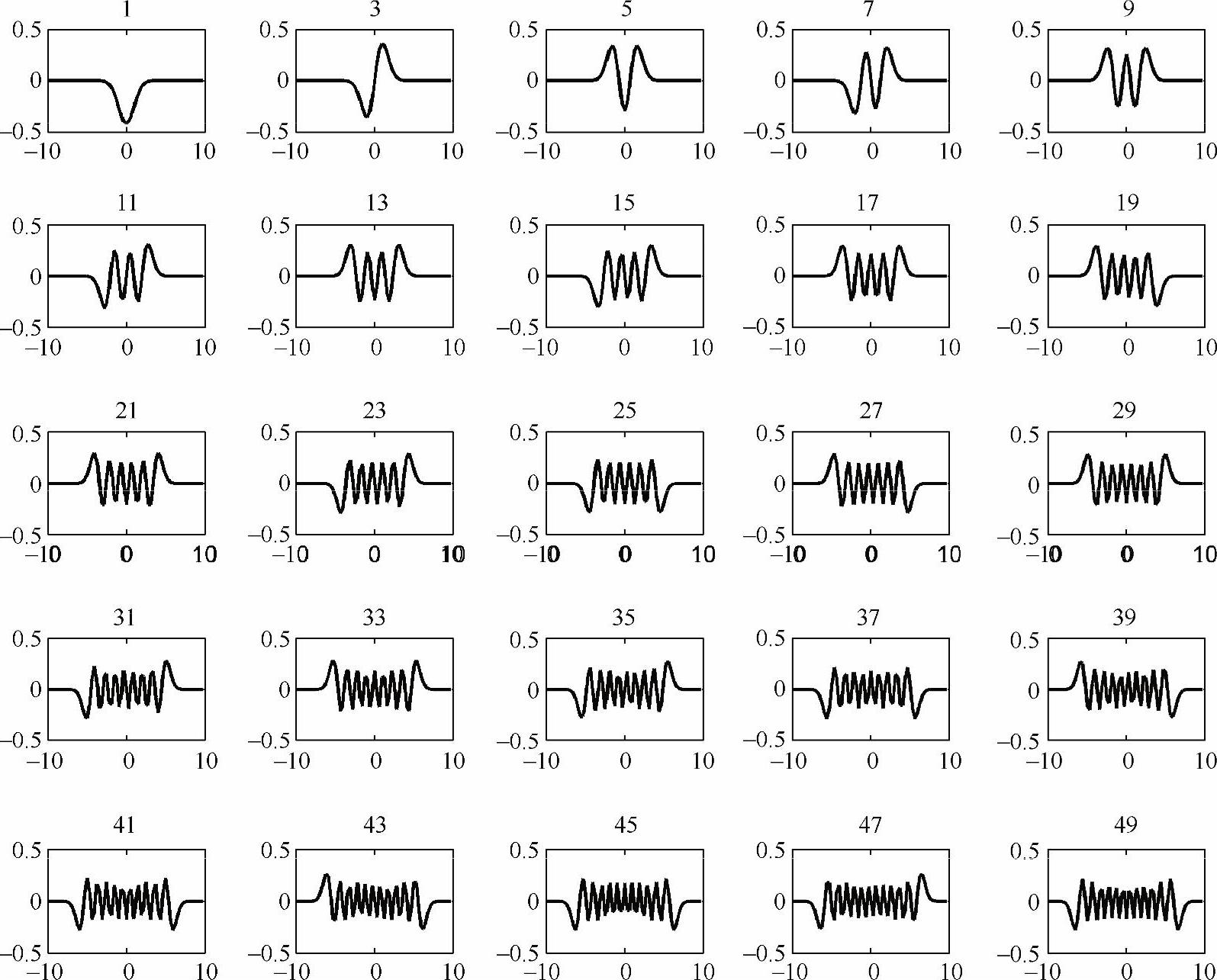
图4-4 一维线性谐振子的前25个特征值和特征函数