Matlab谱方法快速求解微分方程

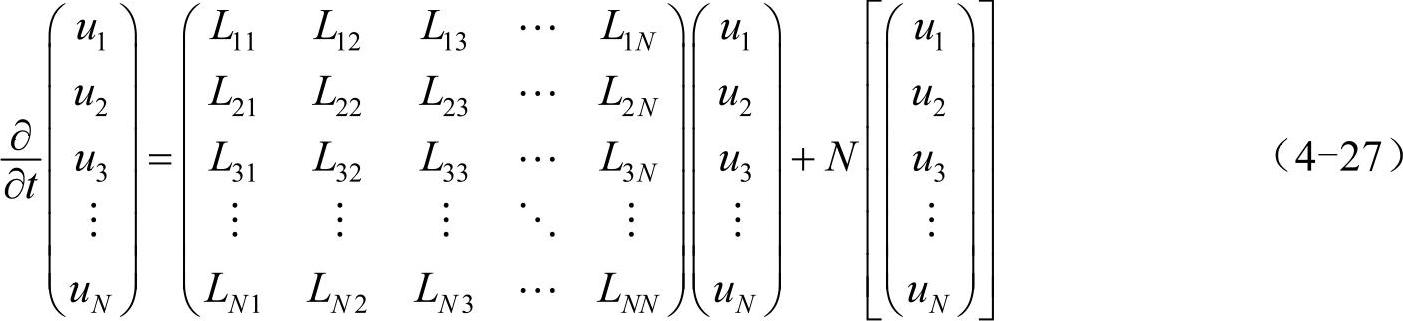
与第3章一样，待求解的偏微分方程的普遍形式为：

其中，u(x,t)为x、t的函数，L代表线性算符，N(u)为非线性项。通过函数代换可将等号左边的n阶导数∂ⁿ/∂tⁿ降到1阶，所以下面分析式（4-26）的求解过程，这与式（4-25）降阶后得到的方程组的解法是一样的。

用谱求导矩阵数值求解式（4-26）的步骤如下：

（1）在x轴上的计算区间内，将x离散化为N个等间距的位置x=(x₁,x₂,…,x_N)^T，相应地，将函数u离散化为N维向量u=(u₁,u₂,…,u_N)^T。

（2）在等号右边，将线性算符L和非线性项N(u)里所有对函数u的求导运算替换为谱求导矩阵与向量u的乘运算，即：∂ⁿu/∂xⁿ→D_N⁽ⁿ⁾u，并将L和N(u)都写成矩阵形式，得到形如式（4-27）的微分方程组。注意，若计算区间长度不是2π，则必须在D_N(n)上乘以缩放系数。

（3）用时间步进法（欧拉法、龙格-库塔法等）数值计算式（4-27）等号左边的∂/∂t，在周期性边界条件下，得到不同t处的向量u。

针对步骤2，这里以L=a·∂²/∂x²+b·∂/∂x+c、N(u)=u³+u³·∂²u/∂x²+f(x)·∂u/∂x为例进行说明，a、b和c分别为常数。对线性算符L，除了将∂ⁿ/∂xⁿ替换为D_N⁽ⁿ⁾之外，还必须在线性算符的常数c上乘以N阶单位矩阵I_N，得到N阶方阵L，即：L=aD_N⁽²⁾+bD_N+cI_N。注意：Matlab对矩阵与常数之间的加法是有特殊定义的，如果忘记在c上乘以I_N会导致错误，因为线性算符矩阵L与向量u相乘Lu=(aD_N(²)+bD_N+cI_N)u=aD_N(²) u+bD_Nu+cu≠(aD_N(²)+bD_N+c)u。对非线性项N(u)，替换∂ⁿ/∂xⁿ为D_N⁽ⁿ⁾时，D_N(n)与向量u之间的乘法是矩阵乘法，在Matlab中用“*”表示。而u³应理解为向量u中的每个元素的立方，这在Matlab中用“.^3”表示。类似地，f(x)·(D_Nu)也应处理为f(x)和向量D_Nu中的每个对应元素的相乘，在Matlab中用“.*”表示。所以此时Lu+N(u)在Matlab中应写为：

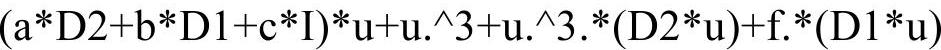
换句话说，只有谱求导矩阵D_N(n)与向量u之间的乘法是矩阵运算，其余的运算均是在矩阵或向量的元素之间进行的。但也有一个例外，由于线性算符L中的常数c在矩阵化时乘了单位矩阵I_N，所以实际上cI_N与向量u之间也是矩阵乘法，这样才能将其与线性算符L中的其他项相加：L=aD_N⁽²⁾+bD_N+cI_N。

若方程式（4-26）再增加一个维度，等号右边包含了u(x,y,t)的∂ⁿ/∂xⁿ和∂ⁿ/∂yⁿ，那么求解步骤中的一些细节就需要推广到二维空间上。在x轴、y轴上的计算区间内分别取等间距的N个位置x=(x₁,x₂,…,xN)T以及y=(y₁,y2,…,yN)T，于是在x^-y平面上的计算区域内就得到了N²个位置的坐标(x₁,y₁),(x₁,y₂),…,(x1,yN),(x2,y1),…,(x2,yN),…,(xN,yN)。相应地，函数u可以被离散化为N阶方阵（第一种形式）或N²维列向量（第二种形式），如式（4-28）、式（4-29）所示：

式（4-28）中，第i行j列的元素u_ij对应的坐标是(x_j,y_i)。列向量（4-29）的第1到第N个元素对应于式（4-28）的第1列，第N+1到第2N个元素对应于式（4-28）的第2列……依此类推，如图4-3所示。另外，可以通过Matlab中的reshape函数在二者间进行转换。

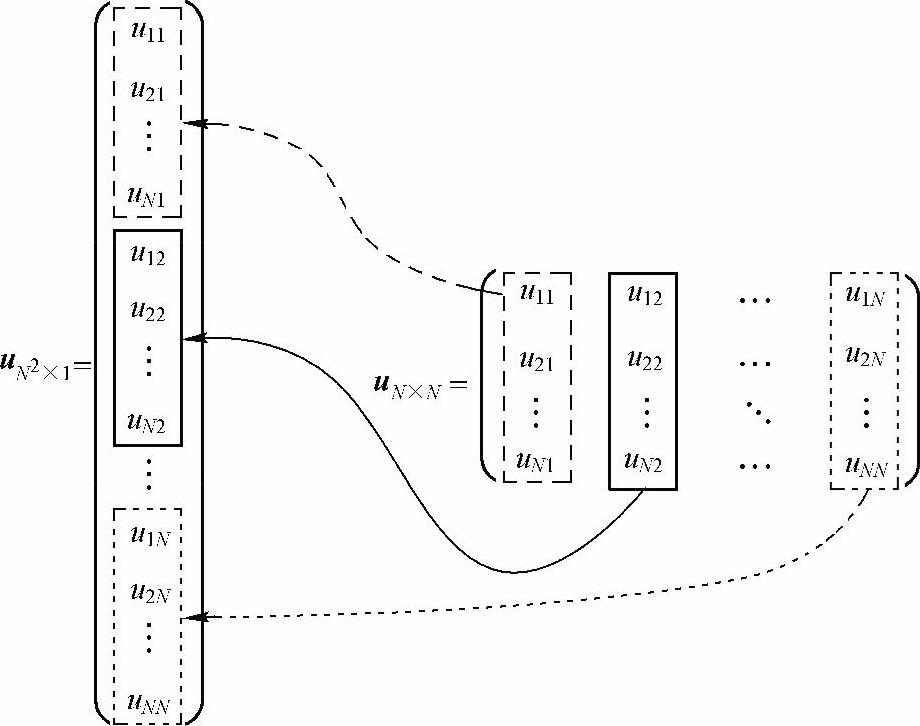
图4-3 函数u的两种离散形式及它们的对应关系

针对函数u的两种离散形式，∂ⁿu/∂xⁿ和∂ⁿu/∂yⁿ的计算方法也大为不同。对于第一种形式，有：

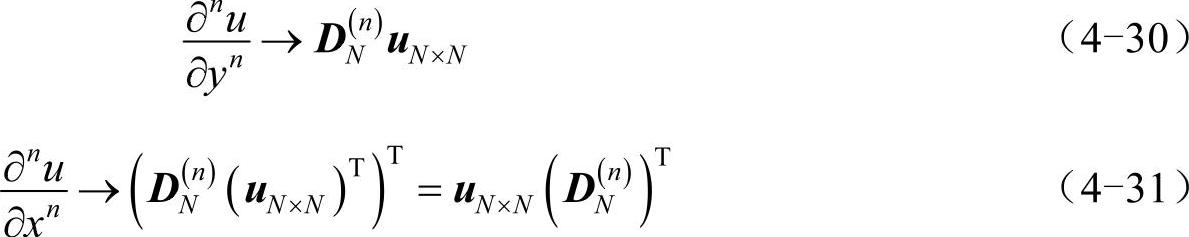
对于第二种形式，有：(www.xing528.com)

其中I_N为N阶单位矩阵，“”代表克罗内克积（Kronecker product），它是两个任意大小矩阵间的运算，可用Matlab中的kron函数实现。若k×l矩阵与m×n矩阵做克罗内克积运算，结果将是km×ln矩阵，并可以被分成k×l块，比如：

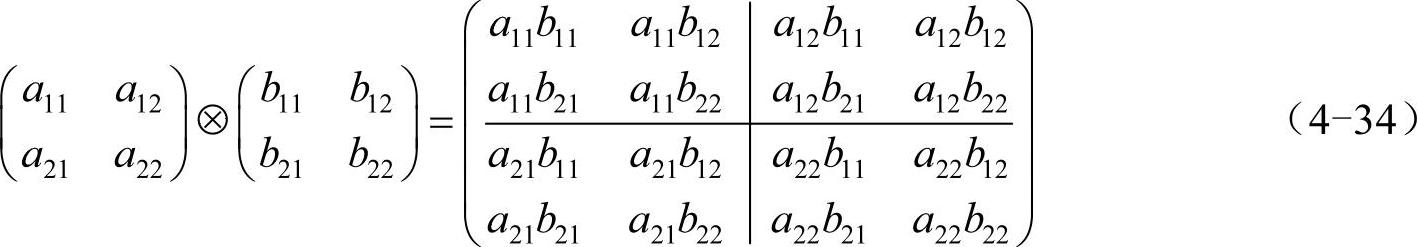
为帮助读者理解，下面给出n=2、N=3时式（4-32）和式（4-33）的一个例子，设D(3²)为：

那么，∂²u/∂y²为：

其中，空白元素均为0，下同。∂²u/∂x²为：

最后，比较函数u在二维平面上的两种离散形式（式（4-28）和式（4-29））以及相应的数值求导过程。从使用的难易度和运算量来讲，前者是远远优于后者的。因为前者最多只出现N阶方阵之间的乘法运算，而后者出现了N²阶方阵与N²维向量的乘法运算。但是在做某些求导过程的逆运算时，就不得不采用第二种离散形式。例如，在x-y二维平面上函数u和v有如下关系：

v=Δu （4-38）

∆为拉普拉斯算符，根据式（4-32）和式（4-33），拉普拉斯算符可以表示为N²阶方阵：

若已知v，求u只需：

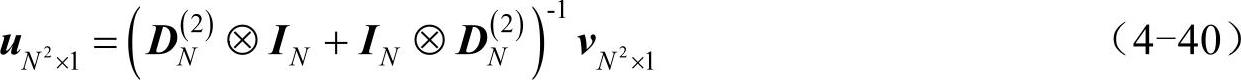
类似地，还可以用此方法求诸如a∂ⁿ/∂xⁿ+b∂^m/∂y^m等导数的逆运算。然而，对于第一种离散形式，有v_N×N=D_N⁽²⁾u_N×N+u_N×N(D_N(2))^T，无法直观、方便地利用D_N⁽²⁾和v_N×N

求得u_N×N。

此外，在二维的特征值问题中，也必须采用第二种离散形式才能求解。