Matlab谱求导矩阵：高效计算微分&误差分析

周期δ函数定义为：

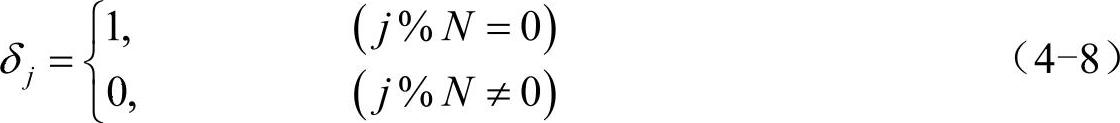
其中，百分号“%”代表求余运算，周期δ函数在j=mN（m为任意整数）时取值为1，其他情况为0，它所对应的横坐标为x_j=jh。利用式（4-3）求周期δ函数的离散傅里叶变换，结果为一常数h：

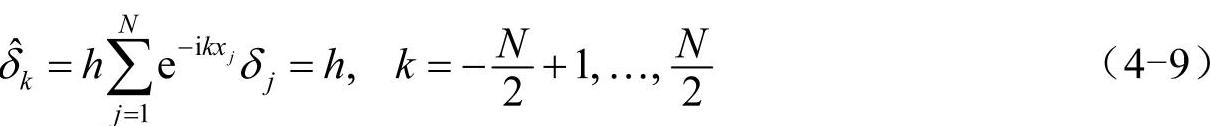
再利用式（4-6）求周期δ函数的插值函数：

由式（4-2），最终得到的周期δ函数的插值函数为周期sinc函数S_N：

可以证明，S_N(x)|_x→0=1。图4-1显示了周期δ函数以及它的插值函数——周期sinc函数S_N(x)，二者的周期均为2π，无论N取值为4还是16，后者都精确、巧妙地经过了前者的所有离散点。

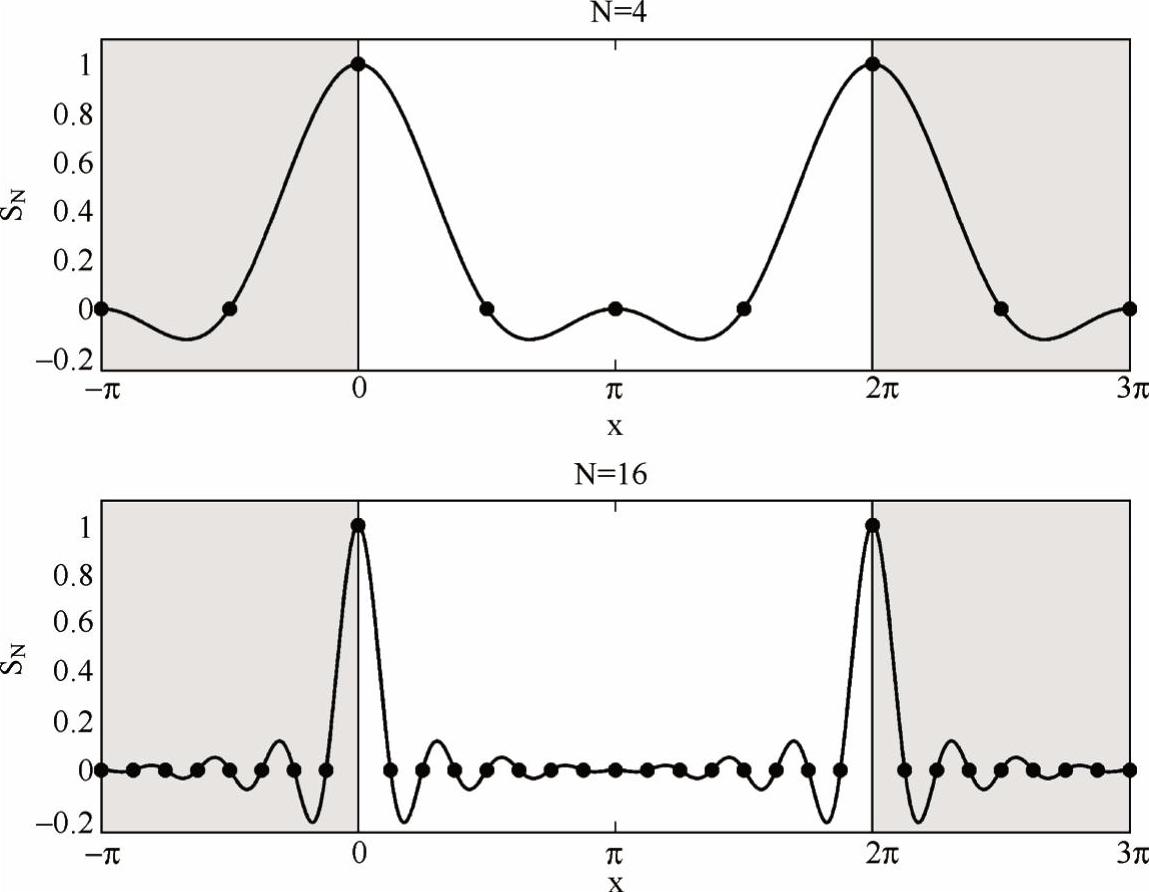
图4-1 曲线为周期sinc函数，黑点为周期δ函数，上下两图分别对应N=4和N=16

若将区间[0,2π]上的序列u₁,u₂,…,u_N写为周期δ函数的线性叠加，即：

那么，将其中的周期δ函数替换为周期sinc函数S_N，就得到序列u₁,u₂,…,u_N的插值函数p(x)：

注意到p(x)就是S_N(x)的线性组合，如果用p(x)来估算序列u₁,u₂,…,u_N在x_j=jh处的1阶导数，则有：

其中，x_j-x_m=(j-m)h。将上式写为矩阵形式：

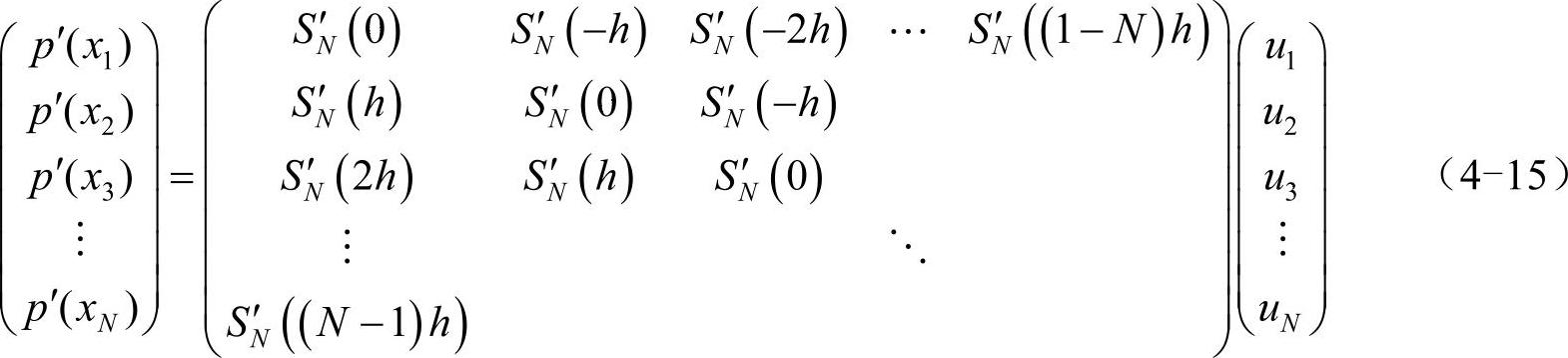
因此，只需在向量(u₁,u₂,…,u_N)^T上乘以一个N阶方阵即可得到由它的谱方法插值函数p(x)的导数组成的向量(p'(x₁),p'(x₂),…,p'(x_N))^T，这个N阶方阵就是谱求导矩阵（spectral differentiation matrix）。下文用D_N来表示1阶N×N谱求导矩阵，D_N(n)表示n阶N×N谱求导矩阵。

周期sinc函数S_N(x)在x_j=jh处的1阶导数为：

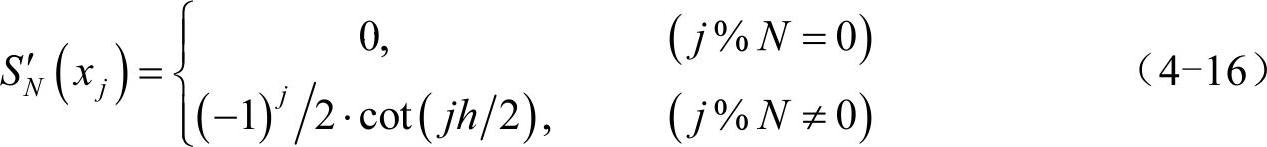
将其代入到式（4-15）中的N阶方阵，得到1阶谱求导矩阵：

类似地，还可以得到高阶谱求导矩阵。周期sinc函数S_N(x)在x_j=jh处的2阶导数为：

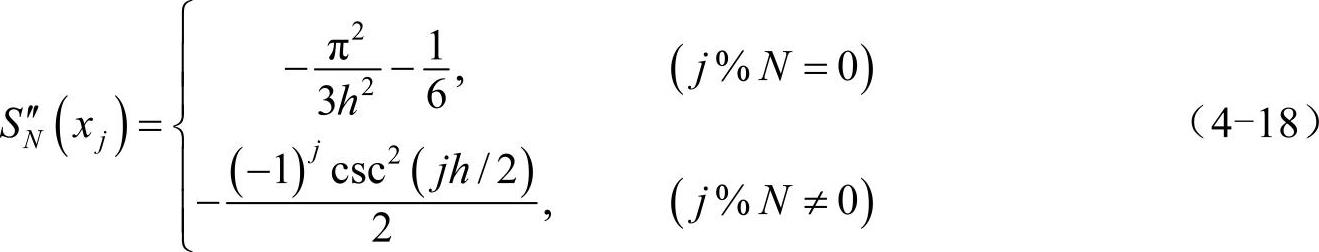(www.xing528.com)

那么，2阶谱求导矩阵为：

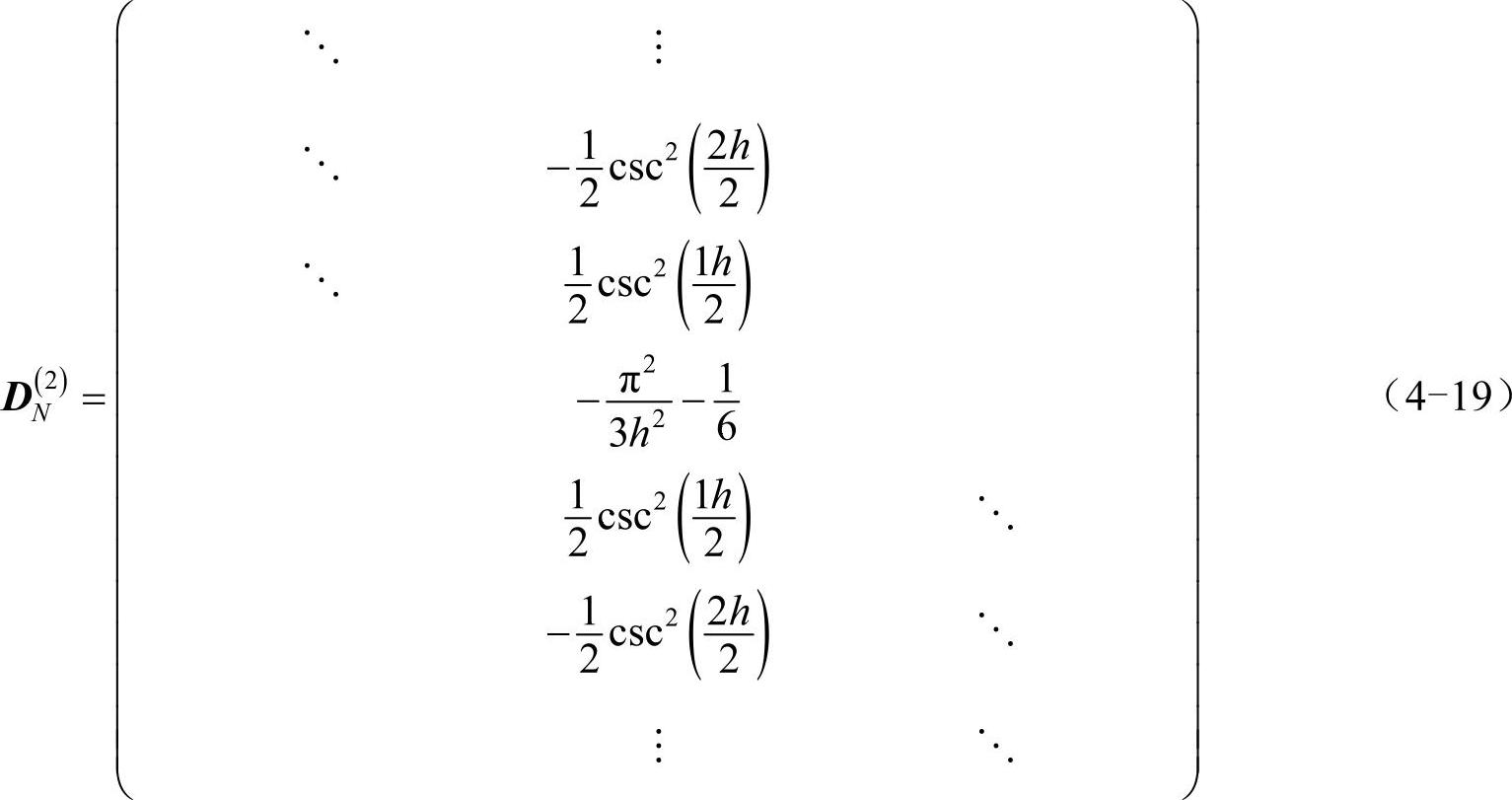
周期sinc函数S_N(x)在x_j=jh处的3阶导数为：

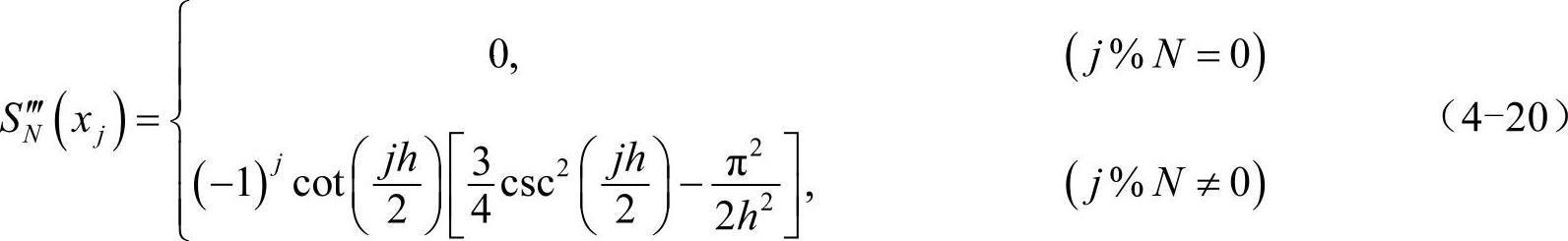
同样得到3阶谱求导矩阵：

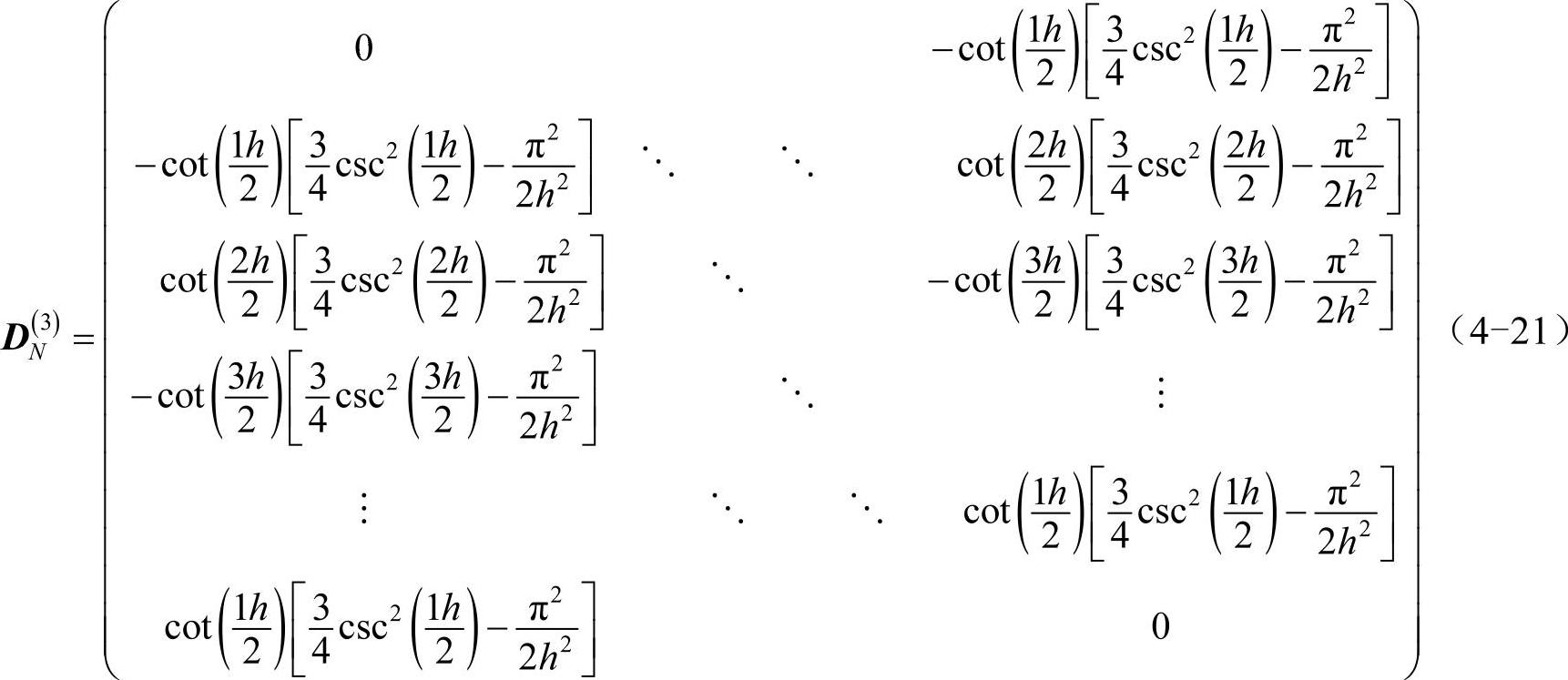
构造n阶谱求导矩阵D_N⁽ⁿ⁾的一般方法为：

（1）求周期sinc函数S_N(x)在x_j=jh处的n阶导数S_N⁽ⁿ⁾(x_j)。

（2）D_N⁽ⁿ⁾的第1列为(S_N⁽ⁿ⁾(x_N),S_N⁽ⁿ⁾(x₁),S_N(n)(x₂),…,S_N⁽ⁿ⁾(x_N-1))^T，第2列为(S_N⁽ⁿ⁾(x_N-1),S_N⁽ⁿ⁾(x_N),S_N⁽ⁿ⁾(x₁),…,S_N⁽ⁿ⁾(x_N-2))^T，第3列为(S_N⁽ⁿ⁾(x_N-2),S_N⁽ⁿ⁾(x_N-1),S_N⁽ⁿ⁾(x_N),…,S_N⁽ⁿ⁾(x_N-3))^T……依此类推。

此外，周期函数S_N(n)(x)的奇偶性是由n的奇偶决定的，这在构造D_N(n)时可以产生一些便利：

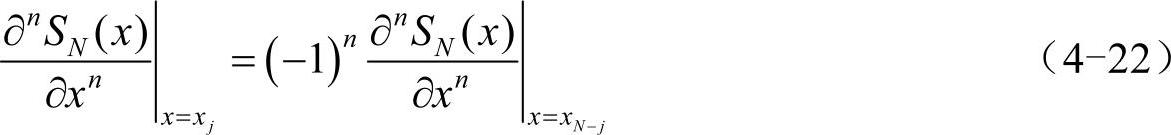
当n为奇数时，必有：

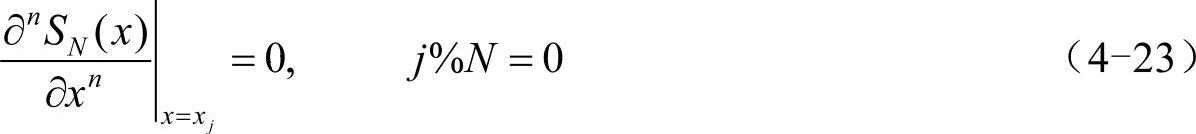
当n为偶数时，S_N⁽ⁿ⁾(x)在x=x_j处（j%N=0）的取值是无穷小/无穷小的形式，需要用洛必达法则求它的极限，即：

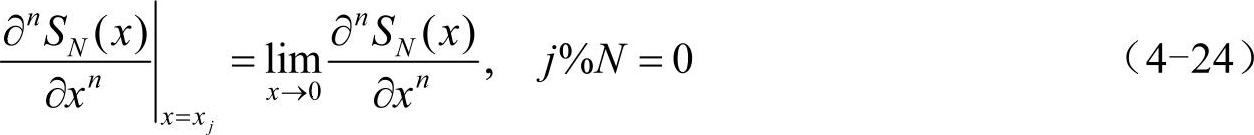
人工计算S_N(x)的n阶导数的工作量随着阶数n的增大而显著增加，比较省时省力的方法是利用Matlab的符号运算功能，调用diff函数和limit函数求导、求极限，并结合toeplitz函数，可实现程序自动生成D_N⁽ⁿ⁾，有兴趣的读者可以自行尝试。

由于谱求导矩阵D_N⁽ⁿ⁾是在计算区间长度为2π的前提下构造的，所以若实际的计算区间长度为L，则必须在D_N(n)上乘以缩放系数才可保证结果正确，即：(2π/L)nD_N⁽ⁿ⁾。

下面给出使用谱求导矩阵D_N、D_N⁽²⁾、D_N⁽³⁾对u(x)=e^sin(πx)求1、2、3阶导数，并与精确解u'(x)=πcos(πx)e^sin(πx)、u"(x)=π²e^sin(πx)[cos²(πx)-sin(πx)]、u'''(x)=π³e^sin(πx)cos(πx)[cos²(πx)-3sin(πx)-1]比较的实例。代码如下：

程序4-1

如图4-2所示，曲线为精确的u(x)、u′(x)、u″(x)和u′′′(x)，点为利用谱求导矩阵计算得到的u′(x_j)、u″(x_j)和u′′′(x_j)。在N的取值仅为32的情况下，用谱求导矩阵计算u(x)=e^sin(πx)的1、2、3阶导数与精确解的最大误差分别在10^-14、10^-12、10^-10数量级。

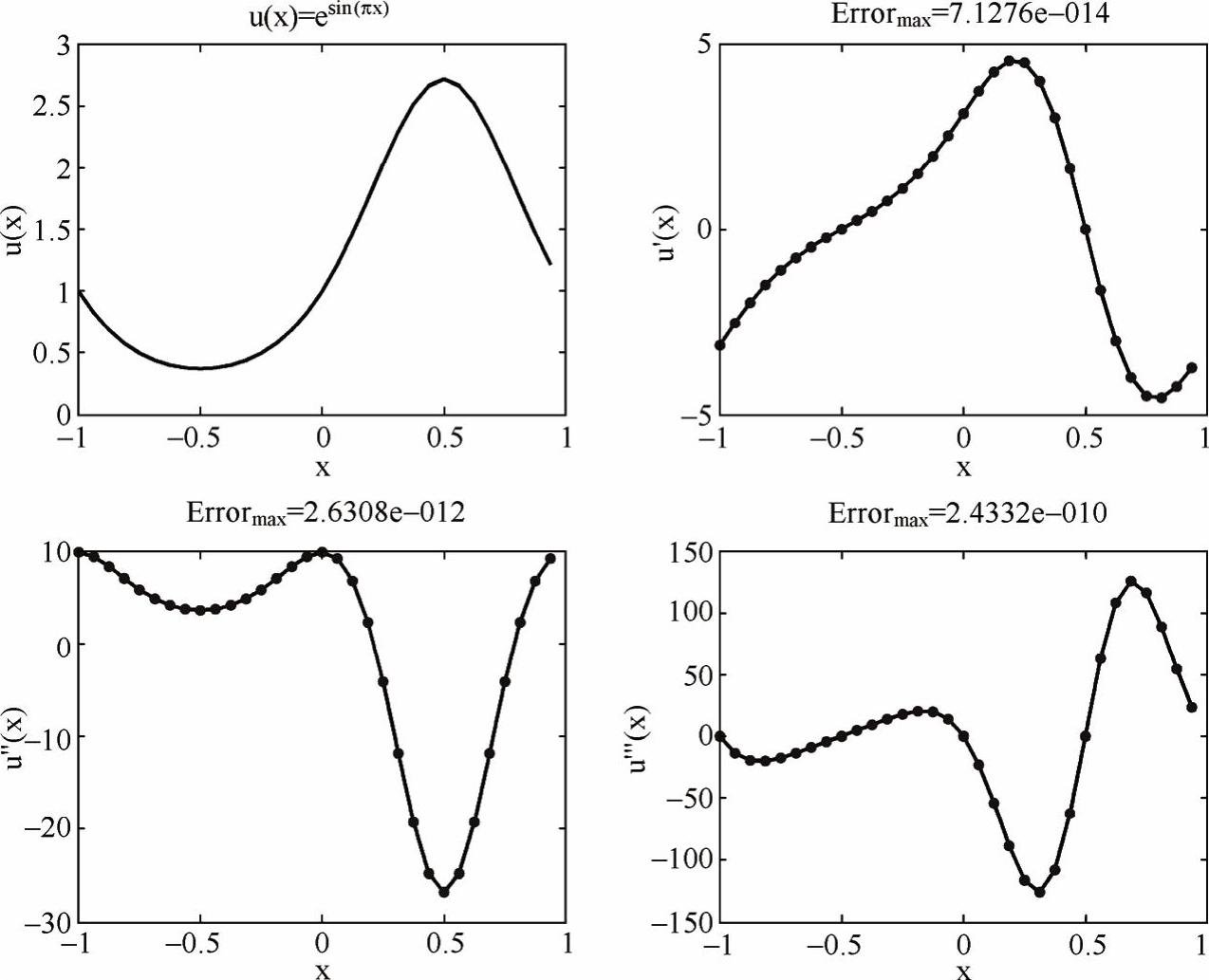
图4-2 用谱求导矩阵计算u(x)=e^sin(πx)的1、2、3阶导数（点）并与精确解（曲线）比较