Matlab谱方法插值：解决周期性边界条件的问题

考虑在区间[0,2π]上、具有周期性边界条件的插值问题。在此区间上间距为h的N个位置x₁,x₂,…,x_N对应的函数值为u₁,u₂,…,u_N。其中，x_j=jh，h=2π/N，即：

在推导前先做3点说明：

（1）选择区间[0,2π]是为了方便讨论，在该区间上得出的结论同样适用于对其平移得到的其他区间（如[-π,π]），并可以通过乘以缩放因子方便地将结论转化到其他长度非2π的任意区间上（如[-L,L]）。

（2）所谓周期性边界条件，是指N个函数值u₁,u₂,…,u_N可等效地看做是无穷多个函数值…,u_-1,u₀,u₁,…,u_N-1,u_N,u_N+1,…的一部分，并存在u_j+m_N=u_j的关系（m为任意整数）。这里把讨论的函数当做周期为2π的周期函数处理。

（3）N的奇偶会导致接下来的推导细节有所差异，但过程是相似的，所以本书只分析N为偶数的情况。

若对序列u₁,u₂,…,u_N做离散傅里叶变换，那么空域（时域）上的间隔h决定了频域上的区间为[-π/h,π/h]（见表3-1）。由式（4-2），该区间也可写为[-N/2,N/2]。本章中的离散傅里叶变换对定义为：

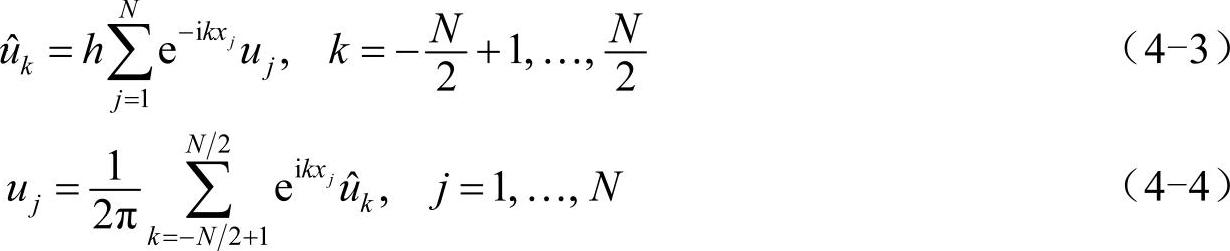(www.xing528.com)

这与第3章给出的Matlab中离散傅里叶变换对的定义略有不同，但实质是一样的。注意到式（4-4）中的频率分量并不是完全对称的，k中有0、±1、±2、……、±(N/2-1)、N/2，却没有-N/2，这在求解插值函数时会引起一些小小的问题。所以，令，并重新定义离散傅里叶逆变换为：

其中，“Σ′”代表求和时在k=±N/2的项上乘以1/2。需要强调的是，式（4-3）和式（4-4）仍然是离散傅里叶变换对的定义，式（4-5）仅是用于确定插值函数p(x)的。求p(x)时需要把式（4-5）中的x_j=jh推广到[0,2π]上的任意实数x，即：

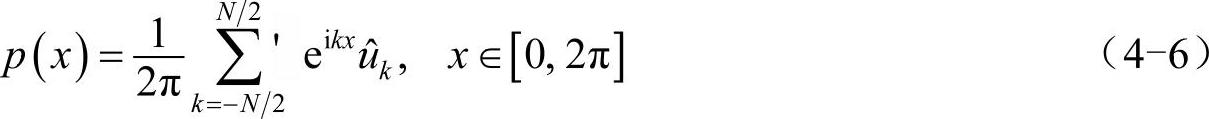
确定插值函数的步骤是这样的：先用式（4-3）将序列u₁,u₂,…,u_N变换为û_-N/2+1,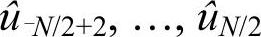，令，再根据序列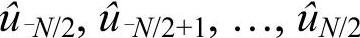通过式（4-6）得到p(x)。这样得到的插值函数p(x)可用来求序列u₁,u₂,…,u_N在x_j处的各阶导数，即：

上面介绍的是通过谱方法计算插值函数p(x)来估算序列u₁,u₂,…,u_N在x_j处的导数的基本原理。接下来，为了把上述过程转化为方便的矩阵运算，采用如下思路：首先求出周期δ函数的插值函数S_N(x)，然后将任意序列u₁,u₂,…,u_N写为周期δ函数的线性组合，进而可把它的插值函数p(x)写为S_N(x)的线性组合，最后找到p(x)和S_N(x)在x₁,x₂,…,x_N处导数的关系并写为矩阵形式，给出针对任意序列u₁,u₂,…,u_N的谱求导矩阵。