【摘要】:取a=1,初始条件为:在数学物理方法中,无界弦的自由振动可由行波法求出解析解,即达朗贝尔公式。首先引入函数v对式进行降阶:对上式等号两边做傅里叶变换,化为偏微分方程组:这样就可以用ode45求解了,详细代码如下:程序3-3主程序代码如下:文件wave1D.m代码如下:计算结果如图3-5所示,初始状态的波形分裂成两半,并分别向x轴正方向和负方向以速度a运动,这和达朗贝尔公式给出的结论是一致的。图3-5 一维波动方程的行波解
对于一根两端固定、没有受到任何外力的弦,若只研究其中的一段,在不太长的时间里,固定端来不及对这段弦产生影响,则可以认为固定端是不存在的,弦的长度为无限大。这种无界(-∞<x<∞)弦的自由振动由式(3-22)描述。

如果保证数值计算的区间足够大,在一定时间内,弦的振动范围始终没有超出计算区间(或可以近似地这么认为),那么就能够放心地使用周期性边界条件。取a=1,初始条件为:

在数学物理方法中,无界弦的自由振动可由行波法求出解析解,即达朗贝尔公式。根据达朗贝尔公式,从t=0开始,u的初始状态2sech(x)将分裂为两个sech形的波,分别向两边以速度a传播出去,即正行波和反行波。下面用傅里叶谱方法求解无界弦的自由振动问题,并与达朗贝尔公式的预测进行比较。首先引入函数v对式(3-22)进行降阶:

对上式等号两边做傅里叶变换,化为偏微分方程组:

这样就可以用ode45求解了,详细代码如下:(https://www.xing528.com)
程序3-3
主程序代码如下:

文件wave1D.m代码如下:
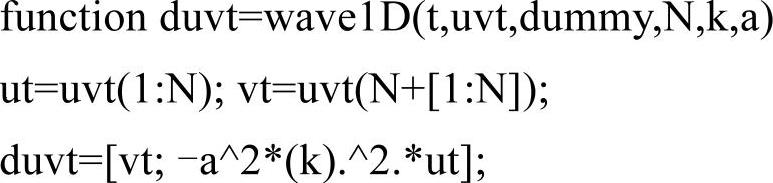
计算结果如图3-5所示,初始状态的波形分裂成两半,并分别向x轴正方向和负方向以速度a运动,这和达朗贝尔公式给出的结论是一致的。
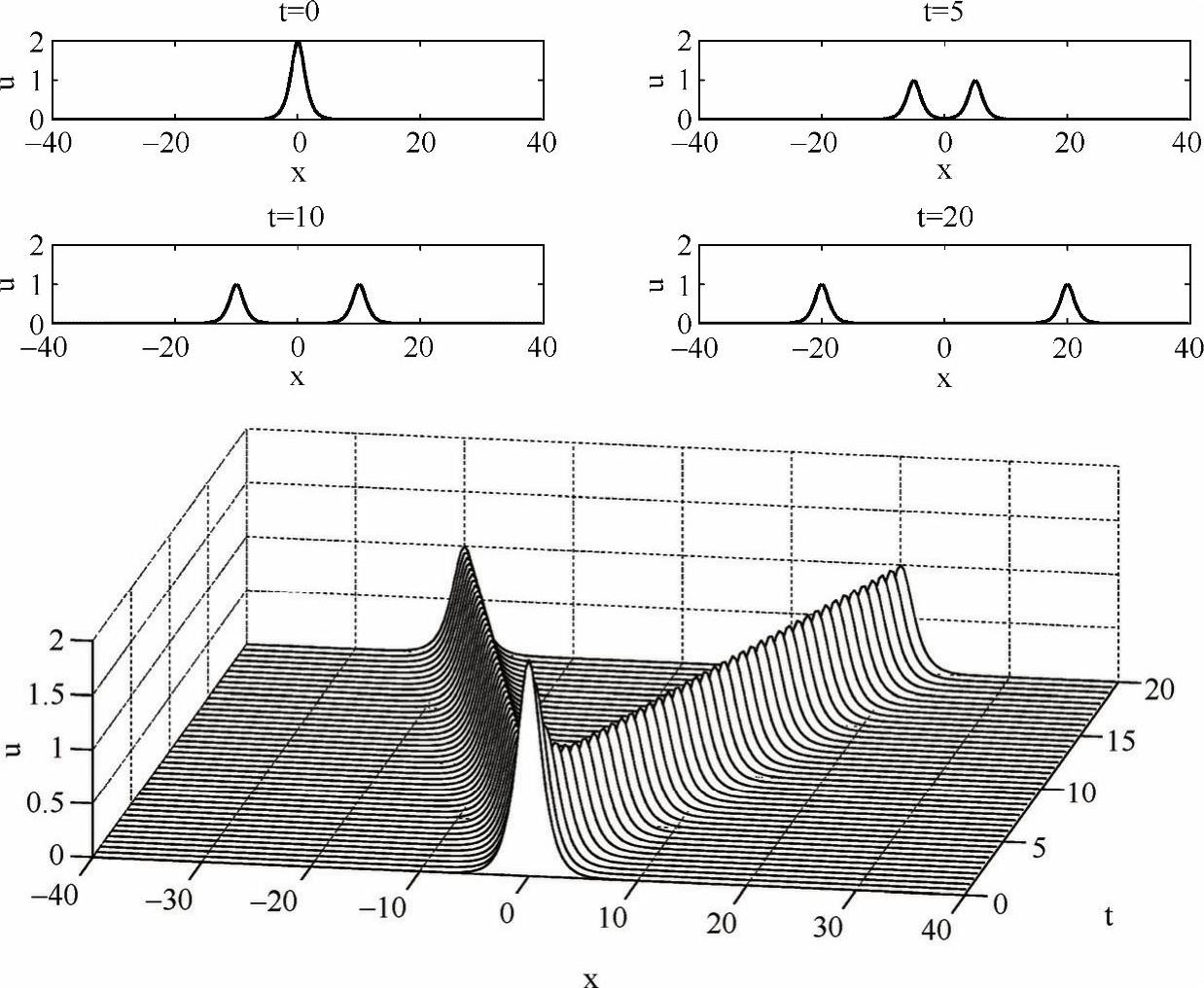
图3-5 一维波动方程的行波解
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




