滤波法解决刚性传输方程的影响

使用傅里叶谱方法时，若频域上关于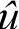的偏微分方程具有刚性，那么其求解速度将大大降低。本小节介绍的滤波法可以提高一部分这种刚性方程的求解速度。

首先分析偏微分方程在傅里叶谱方法中是如何被引入刚性的，以超扩散方程（hyper-diffusion equation）为例，见式（3-15）：

对其做傅里叶变换后，得：

如果x域上的计算区间宽度L=2，区间上数据点的数量N=256，那么|k|的最大值为Nπ/L≈400，则(k_max)4≈2.6×10¹⁰，假设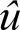在高频k_max处的数量级很小，不妨令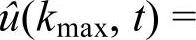10^-6，有：

等号右边的数量绝对值很大，这将导致ode45（其他变步长算法亦如此）在计算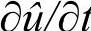时必须采用很小的步长∆t才能把误差控制在可接受范围内，因此显著增加了运算时间，这就是式（3-16）的刚性带来的计算困难。此外，采用过小的L、过大的N都会加剧这一问题。

一般地，对式（3-12）进行傅里叶变换得到式（3-13）之后，如果线性项α(k)û中的高频部分造成了方程的刚性问题，可用滤波法解决。方法如下：偏微分方程的线性部分是可以解析求解的，因此在式（3-13）两端乘上积分因子e^-α(k)t，整理得：(www.xing528.com)

将前两项合并，即：

令ŵ=e^-α(k)tû，则：

也可以写成以下形式，数值计算出式（3-20）或式（3-21）的结果再利用关系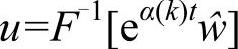将ŵ化为u即可。

这样就通过引入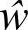将线性项中的刚性削弱了。然而非线性项中也可能存在刚性，以致影响运算速度，所以滤波法只是对傅里叶谱方法中的一部分刚性方程有效。实际上，较之傅里叶谱方法，滤波法对计算时间的节省只有在空域上最高阶导数的维度大于2的时候才能体现出来。