Matlab谱方法：微分方程高效解法

对于F[u′(x)]，由傅里叶变换的定义和分部积分法，得到：

当|x|→∞时，u(x)→0，则：

类似地，可以得到：

其中u⁽ⁿ⁾(x)代表u(x)的n阶导数。上式的意义在于：函数的求导运算在傅里叶变换的作用下，可转化为相对简单的代数运算，即：u⁽ⁿ⁾(x)=F^-1{(ik)ⁿF[u(x)]}。正是基于此原理，傅里叶谱方法（Fourier spectral method）利用傅里叶变换将偏微分方程中空域（space domain）或时域（time domain）上的求导运算简化为频域（spectral domain）上的代数运算，求解后再通过傅里叶逆变换得到空域或时域上的结果。在代码层面上，Matlab提供的快速傅里叶变换函数fft、逆变换函数ifft以及强大的矩阵运算能力也为简洁、优雅地实现傅里叶谱方法奠定了基础。

3.1.1小节已经提到，fft输出结果在频域上的顺序是颠倒的，经过fft函数变换后的序列在k轴上所对应的坐标是：

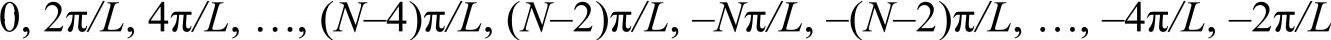
利用傅里叶谱方法求导时，在代码中通常使用顺序颠倒的频域坐标，以求序列u的一阶导数数值解为例：ifft(i^*k.^*fft(u))。其中，变量k是由Matlab语句(2^*pi/L)*[0:N/2-1-N/2:-1]生成的顺序颠倒的频域坐标，这样做是为了免去调用fftshift和ifftshift的步骤。

(www.xing528.com)

图3-2 傅里叶谱方法求u(x)=e^sin(πx)的1、2、3阶导数并与解析解比较

下面用实例说明傅里叶谱方法求u(x)=e^sin(πx)的1、2、3阶导数的过程，并与解析解u'(x)=πcos(πx)e^sin(πx)、u"(x)=π²e^sin(πx)[cos²(πx)­sin(πx)]、u'''(x)=π³e^sin(πx)cos(πx)[cos²(πx)­3sin(πx)­1]相比较，得到的最大误差分别在10^-14、10^-13、10^-11数量级，如图3-2所示。代码如下：

程序3-2

式（3-9）也可写为：

若把u(x)看成是对u(n)(x)做n次积分的结果，式（3-10）就具有了求不定积分的意义。当然，这里暂时没有考虑积分常数的问题。与式（3-9）比较可知，求n阶导数相当于在频域上乘以(ik)n，相应地，做n次积分就是在频域上除以(ik)n。需要强调的是，如此计算积分会出现一个问题，那就是k为0时会导致式（3-10）出现无穷大。在编写程序时有两种解决办法：

（1）将k的0值修改为很小的数，如：10^-6。

（2）在分母上加一个很小的数，防止分母为0，即：(ik)ⁿ+eps。其中，eps是Matlab中的浮点相对误差限，它的值在10^-16数量级。这样，就通过引入微小的误差避免了分母为0的问题。