高效解法：谱方法下的快速傅里叶变换

对于在(­∞,∞)有定义且绝对可积、并在任一有限区间上满足狄利克莱条件的函数u(x)，傅里叶变换（Fourier transform）及其逆变换（inverse Fourier transform）定义为：

上述定义式给出了一个傅里叶变换对（Fourier transform pair），本书中将它们记为û(k)=F[u(x)]和u(x)=F^-1[û(k)]。实际上，傅里叶变换对的定义并不是唯一的，两个定义式中的系数可以随意修改，只要它们的积为1/2π即可。此外，定义式中的e^-ikx和e^ikx（称为积分变换的核）也可以互换。容易知道，u(x)先后经过傅里叶变换及其逆变换仍将得到它本身，即：u(x)=F^-1{F[u(x)]}。在物理上，若研究对象为空间上的信号分布u(x)，x代表空间坐标，那么k就是波数（2π长度上波长的个数，代表信号在空间上的变化速度），û(k)称为波数谱；类似地，若将上式中的坐标x和波数k代换成时间t和角频率ω，研究对象就成了时间上的信号u(t)，其傅里叶变换就是频谱û(ω)，通过类比可知波数k其实就是一种空间上的频率。傅里叶变换及逆变换是空域（或时域）与频域之间的转换工具。

当函数u为二维函数时，将x方向上和y方向上的傅里叶变换记为F_x[]和F_y[]，并在变换后的函数上加“^”、“~”进行区分，如：，,y)]，其中k_x、k_y为x、y方向的波数。在二维情况下，默认F[]和F^-1[]分别代表二维傅里叶变换及逆变换，即F[]=F_y{F_x[]}或F_x{F_y[]}、F^-1[]=F_y^-1{F_x^-1[]}或F_x^-1{F_y^-1[]}，并有：

通常来讲，若不对“傅里叶变换”加任何限定，那么它指的就是连续傅里叶变换，也就是针对定义在无限区间内的连续函数u(x)的傅里叶变换，这是在理想条件下的数学定义。在实际应用中，尤其是计算机的信号采样、信号处理当中，信号是离散的、有限的，离散傅里叶变换（discrete Fourier transform）就是针对这一情况提出的。在Matlab中，对于序列u₁,…,u_j,…,u_N的离散傅里叶变换及逆变换定义为：

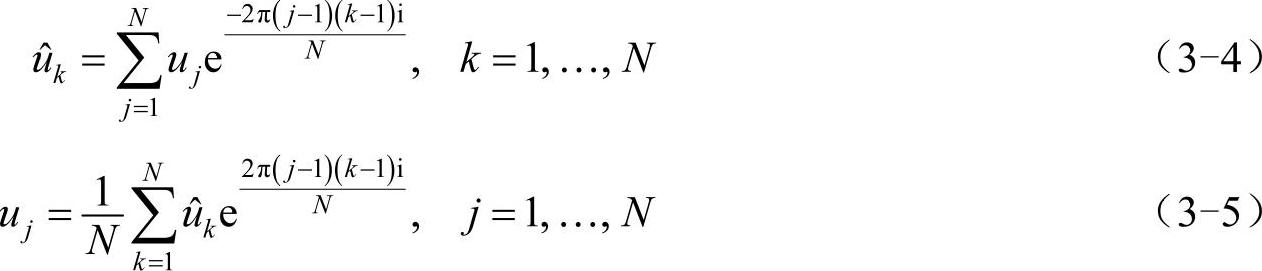
同样，上述定义中的归一化系数也可以有其他选择，但它们的乘积必须为1/N。如果将序列u₁,…,u_j,…,u_N看作等间隔空间（时间）点上的信号幅度值，那么经过离散傅里叶变换得到的序列,…,,…,就是其相应的频谱信息。通过定义式（3-4）和（3-5）容易得到和u_j=u_j+N，这就是说，离散傅里叶变换已经隐含了周期性边界条件，它假设待做离散傅里叶变换的离散信号在周期为2π的周期域上。在实际运算中，人们不直接采用上述离散傅里叶变换的定义式进行计算，而是使用快速傅里叶变换（fast Fourier transform）算法，此算法是二十世纪六十年代中期由Cooley和Tukey提出的，被誉为二十世纪最伟大的十大算法之一。离散傅里叶变换定义式的运算量（arithmetical operation）是O(N²)，而快速傅里叶变换可将运算量降低到O(NlogN)。特别是当N很大的时候，NlogN的增长速度仅接近于N，可以大大地节省计算时间。但是，为了获得较高的运算速度，待变换序列的元素数量必须是2ⁿ个，即其个数必须为2、4、8、16、32、64……。

在Matlab中，fft和ifft函数实现基于快速傅里叶变换算法的一维离散傅里叶变换及逆变换。fft函数的一般调用语法为：

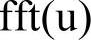
若u为一向量，则fft返回其离散傅里叶变换的结果。若u为一矩阵，则fft返回矩阵中每一列的离散傅里叶变换。若要计算矩阵u中每一行的离散傅里叶变换，只需调用fft(u,[],2)即可，它速度比fft(u.').'更快一些。ifft函数的调用语法与fft函数完全一样。

若输入fft函数的空域信号序列u₁,…,u_j,…,u_N在x轴上的坐标间隔是L/N，相应的横坐标x可认为是：

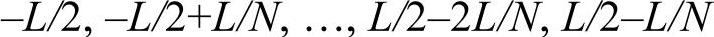
注意，fft函数输出的序列û₁,…,û_k,…,û_N所对应的频率并不是按照从小到大的顺序排列的，而是非负频率对应于前半部分序列，负频率对应于后半部分序列，即：

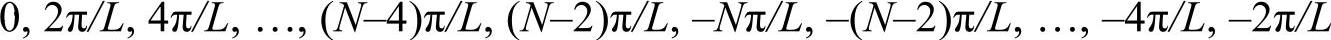
因此Matlab提供了fftshift函数，用于调整fft输出序列的顺序。也就是说，fftshift(fft(u))所对应的频率才是按照递增顺序排列的：

空域坐标与频域坐标的关系如表3-1所示，不难发现，空域上的两点间隔和频域区间长度成反比，乘积为2π，频域上的两点间隔和空域区间长度的关系亦如此。(www.xing528.com)

表3-1 空域坐标与频域坐标的关系

此外还有ifftshift函数用于进行与fftshift函数相反的操作。实际上，fftshift函数的作用仅是让fft的输出结果变得更易于观察，若还需要用ifft函数将频谱信息还原回空域信号，就必须在使用fftshift之后再用ifftshift函数将序列的顺序恢复，否则得不到正确结果。如果不是为了分析频谱信息，而是用下文即将介绍的傅里叶谱方法处理导数和微分问题，则大可不必使用fftshift和ifftshift函数调整序列的顺序，以减少代码冗余、节约时间。

基于快速傅里叶变换算法的二维离散傅里叶变换及逆变换由fft2、ifft2函数实现，一般调用语法为：

它返回矩阵u的二维傅里叶变换，等效于fft(fft(u),[],2)。ifft2与fft2的调用语法一样，就不再赘述。

fftshift函数的调用语法为：

若u为一向量，它将u左右两半互换并返回。若u为一矩阵，则它将u的第1、3象限互换以及第2、4象限互换并返回。此外，若要互换矩阵u的上下两半，可以调用fftshift(u,1)。要互换矩阵u的左右两半，只需调用fftshift(u,2)。ifftshift函数与fftshift函数功能完全相反，调用语法相同，这里不再重复。

接下来以实例说明fft等函数的用法。众所周知，sinc²函数的傅里叶变换是tri函数（三角形函数），即：

取a=1，实现函数sinc²(x)傅里叶变换的代码如下：

程序3-1

代码的执行结果如图3-1所示，sinc²形信号经过fft函数变换所得频谱的顺序出现颠倒，低频成分在两端，高频成分在中间。随后经过fftshift函数调整顺序，低频成分被置于频谱中间，其中的求绝对值函数abs用来得到频谱的振幅。再使用ifftshift函数还原频谱顺序并用ifft函数做傅里叶逆变换，就得到了最初的sinc²函数。注意到三角形函数的幅度与式（3-6）不相符，这并不是计算错误，而是快速傅里叶变换对fft和ifft的系数选取不同造成的，这一差异丝毫不影响后面即将讨论的傅里叶谱方法。

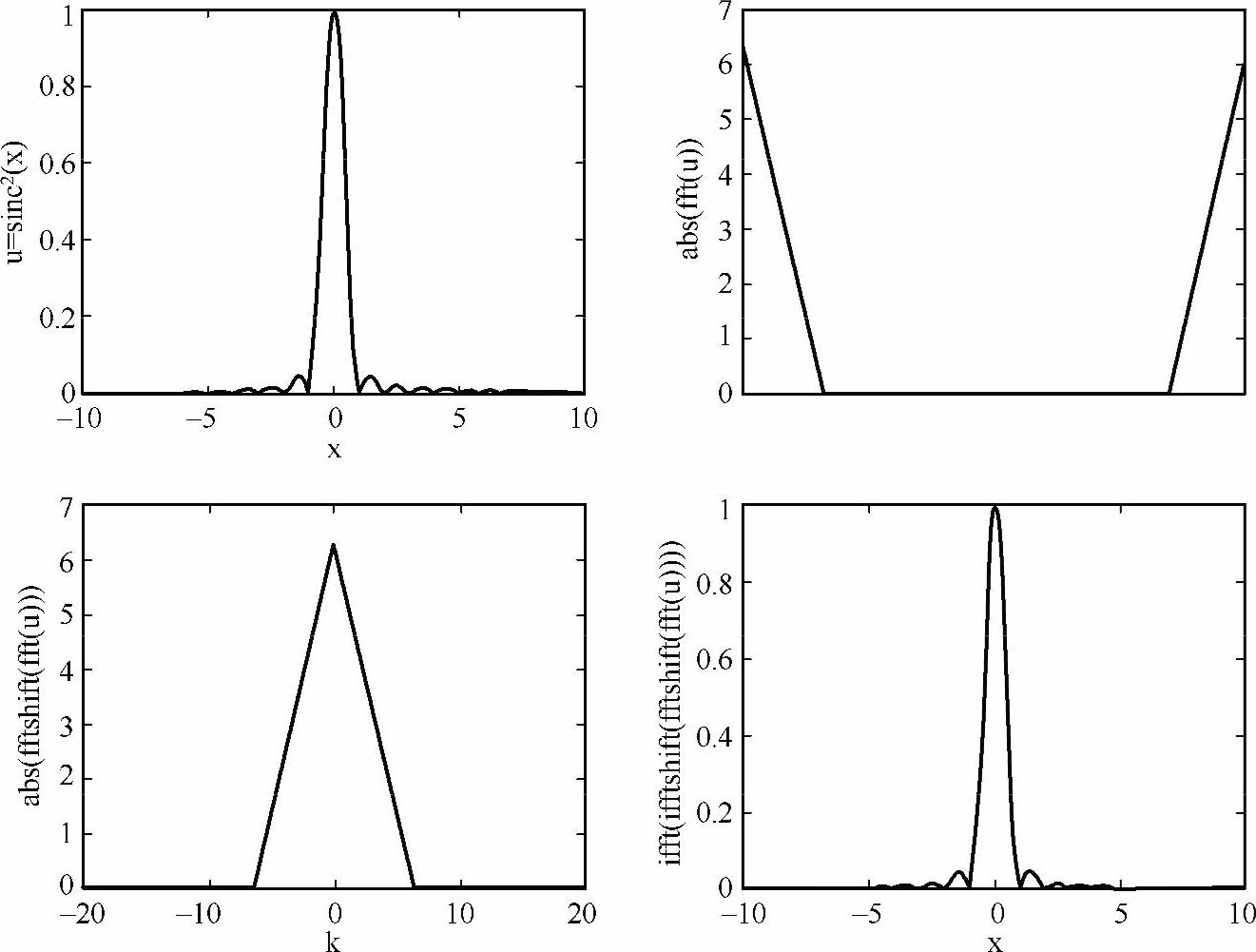
图3-1 fft、ifft、fftshift、ifftshift函数的用法