高效解法：Matlab谱方法解二维特征值问题

考虑单位圆内拉普拉斯算符的特征值问题：

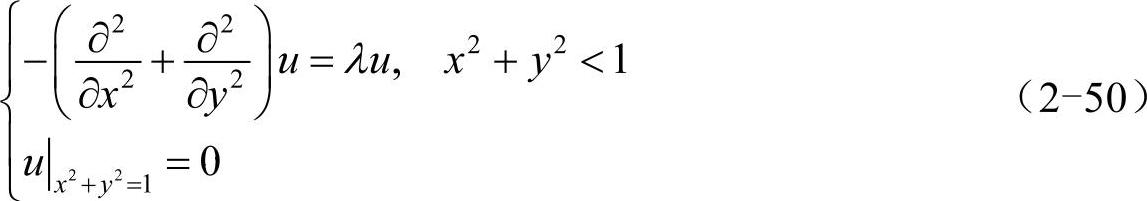
求解步骤如下：

启动偏微分工具箱，点击按钮，按住Ctrl键同时鼠标左键在原点按下并拖曳到合适位置画一个近似的单位圆。双击此圆打开图形参数设置对话框，将X-center、Y-center、Radius分别设置为0、0、1，点击OK。

点击按钮进入边界模式，双击每一段边界，打开边界条件设置对话框，选择狄利克莱边界条件“Dirichlet”，填入h=1、r=0，并点击OK。

点击按钮打开方程参数设置对话框，方程类型选特征值问题“Eigenmodes”。比较式（2-44）和式（2-50），可知参数取值如下：c=1、a=0、d=1。填入参数后点击OK。

点击Solve菜单中的Parameters选项，打开求解参数设置对话框。在此处可以设置特征值的搜索范围，这里以0到100之间的特征值为例，填入[0100]并点击OK。

点击按钮初始化三角网格，随后再根据需要多次点击按钮加密三角网格。

点击按钮求解方程，程序默认显示最小的特征值和其所对应的特征函数。(www.xing528.com)

点击按钮打开画图设置对话框，勾选Color、Height(3-D plot)，此外可以在Eigenvalue后的下拉菜单中选择特征值（由小到大排列），如图2-35所示。点击Plot后得到该特征值及其所对应的特征函数的彩色三维图，如图2-36所示为第6个特征值和特征函数。

图2-35 选择特征值

至此，利用偏微分工具箱求解四类基本偏微分方程的方法就介绍完了。实际上，偏微分工具箱还有针对性地为一些领域的具体问题提供了解决方案，如：结构力学、静电学、电磁学、热传导等，但限于篇幅，本书中就不再介绍，更多使用方法参见偏微分工具箱Help菜单中的内容。除了图形界面的工具之外，偏微分工具箱也提供了命令行的调用方式，可直接编写m文件求解偏微分方程，这使得偏微分工具箱更容易被其他程序调用并进一步处理结果。

偏微分工具箱的界面友好，且边界条件和求解区域可随意选取，这些优点毋须多言。但它依然不可避免地存在一些不足：只能求解特定类型的偏微分方程，为获得高精度必须提高网格密度，导致运算量提高。这些不足都将在后续章节介绍的谱方法中得到改进。

图2-36 第6个特征值所对应的特征函数