二维波动方程的高效解法：Matlab谱方法实现

考虑如下二维波动方程的定解问题，取a=0.1：

可近似认为上式描述了一个四周被固定的正方形弹性薄膜在中心被拉起并突然释放之后的过程，u为薄膜上每个点的位移。求解步骤如下：

和前面类似，先启动偏微分工具箱，点击按钮，按住Ctrl键同时点击并拖曳鼠标左键画一个正方形。双击此正方形打开图形参数设置对话框，将Left、Bottom、Width、Height分别设置为-1、-1、2、2，点击OK。

点击按钮进入边界模式，双击每一段边界，打开边界条件设置对话框，选择狄利克莱边界条件“Dirichlet”，填入h=1、r=0并点击OK。

点击按钮打开方程参数设置对话框，方程类型选双曲型“Hyperbolic”。比较式（2-43）和式（2-49），可知参数取值如下：c=0.1、a=0、f=0、d=1。填入参数后点击OK。

点击Solve菜单中的Parameters选项，打开求解参数设置对话框。其中，Time一栏为求解的时间区间，填入0:1代表从t=0计算到t=1。u(t0)一栏为u的初始条件，这里填入exp(-20^*(x.^2+y.^2))。u′(t0)一栏为∂u/∂t的初始条件，填入0即可。其余两栏为相对误差和绝对误差，一般采用默认设置，最后点击OK。(www.xing528.com)

点击按钮初始化三角网格，随后再根据需要多次点击按钮加密三角网格。

点击按钮打开画图设置对话框，勾选Color、Height(3-D plot)、Show mesh，点击Plot，可得带网格的彩色三维图，如图2-34所示为t=1时的数值解。

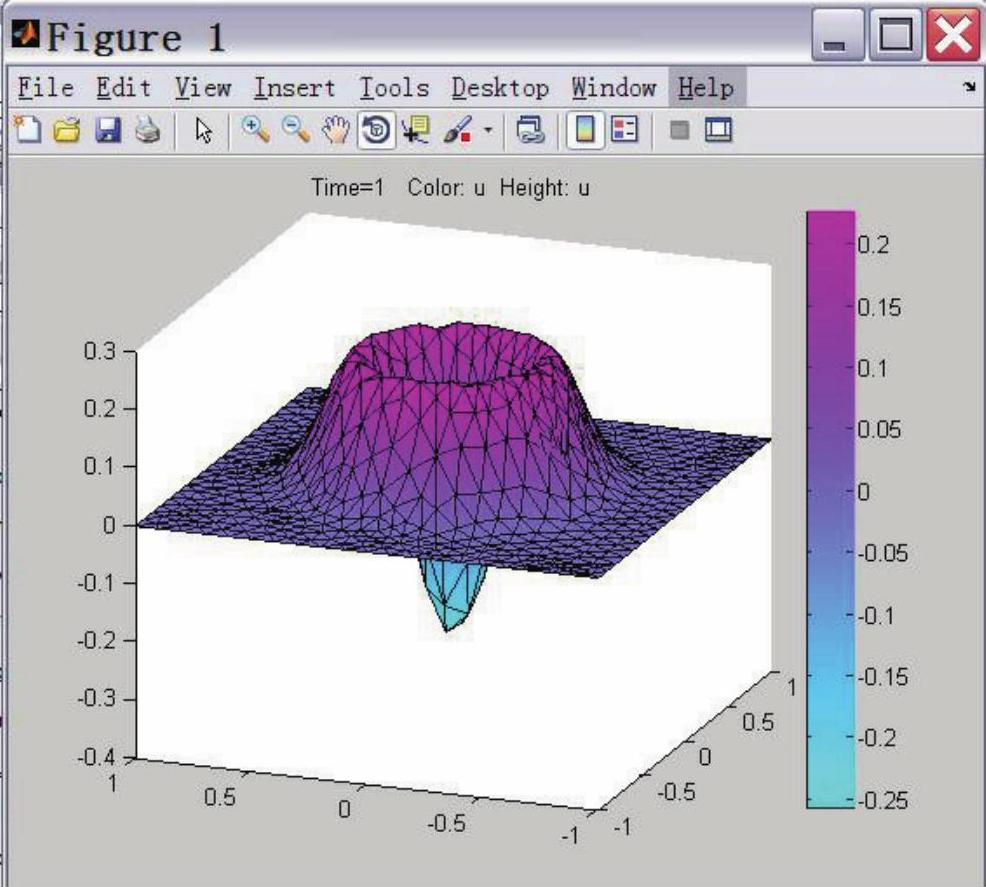
图2-34 带网格的彩色三维图

如果在Solve菜单中Parameters选项的Time一栏填入0:0.01:1，并在画图设置对话框勾选Color、Animation，点击Plot，将会得到数值解的彩色动画。0:0.01:1代表在t=0和t=1之间，每隔0.01就输出一幅图作为动画的一帧。Animation后方的Options选项可设置动画帧率、重复播放次数。