高效解法：二维泊松方程的谱方法

考虑单位圆上的泊松问题：

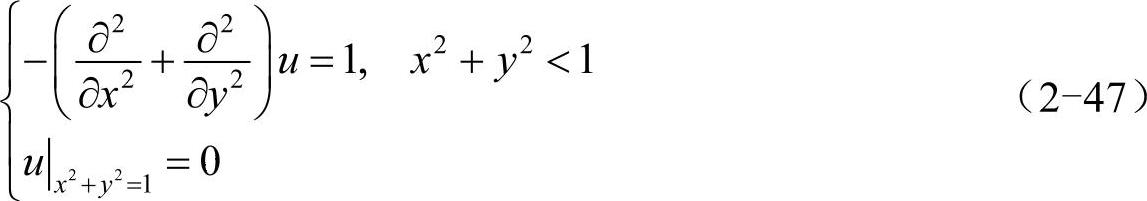
其解析解为u=(1-x²-y²)/4，求解步骤如下：

首先启动偏微分工具箱，点击按钮，按住Ctrl键同时鼠标左键在原点按下并拖曳到合适位置画一个近似的单位圆。双击此圆打开图形参数设置对话框，将X-center、Y-center、Radius分别设置为0、0、1，点击OK，这样就得到了作为求解区域的单位圆。

点击按钮进入边界模式，双击单位圆的每一段边界，弹出边界条件设置对话框，默认为h=1、r=0的狄利克莱边界条件“Dirichlet”，这正是所需要的，所以不用做任何修改，点击OK。如果若干段边界的边界条件是一样的，可按住shift键同时选择多段边界，双击后一起设置边界条件。

点击按钮打开方程参数设置对话框，方程类型选椭圆型“Elliptic”。比较式（2-41）和式（2-47），可知参数取值如下：c=1、a=0、f=1。填入参数后点击OK。

点击按钮初始化三角网格，随后可根据需要多次点击按钮加密三角网格，程序界面的最下方将会显示网格的结点数和三角单元数。若选择Mesh菜单下的Show Node Labels，将显示结点编号，如图2-26所示为初始网格及其结点编号。

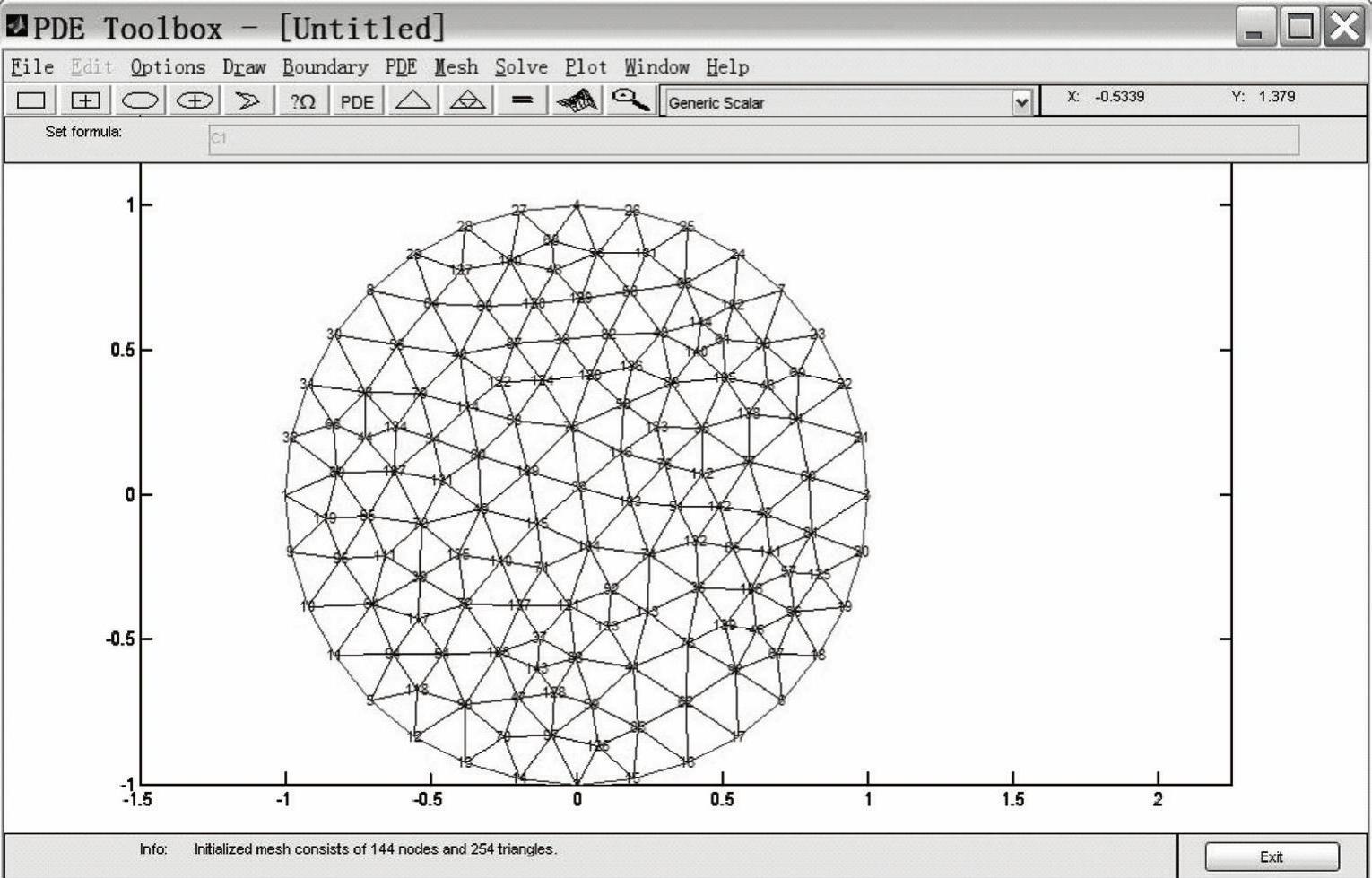
图2-26 显示结点编号

要导出网格剖分的数据信息，点击Mesh菜单下的Export Mesh，出现如图2-27所示的对话框。在其中填入用来存放点、边、三角形数据的变量名（默认为points、edges和triangles的首字母p、e和t），之后点击OK即可将数据导出到Matlab的workpace相应变量中。

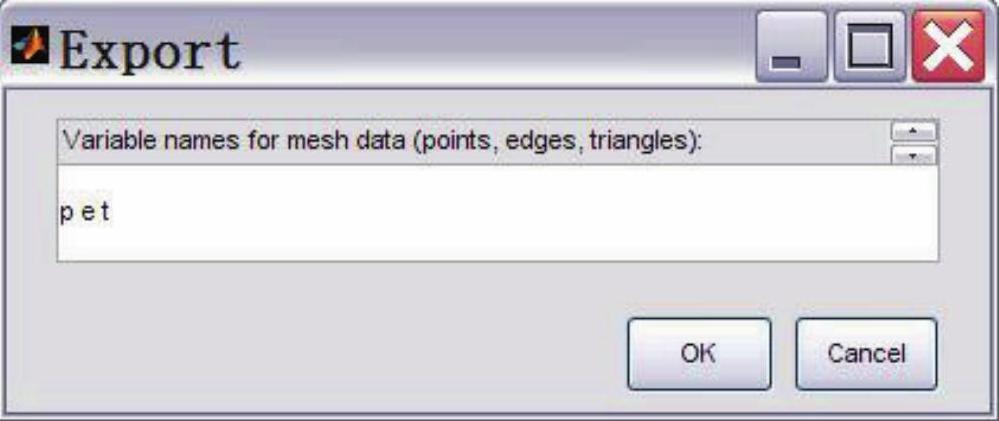
图2-27 导出网格剖分的数据

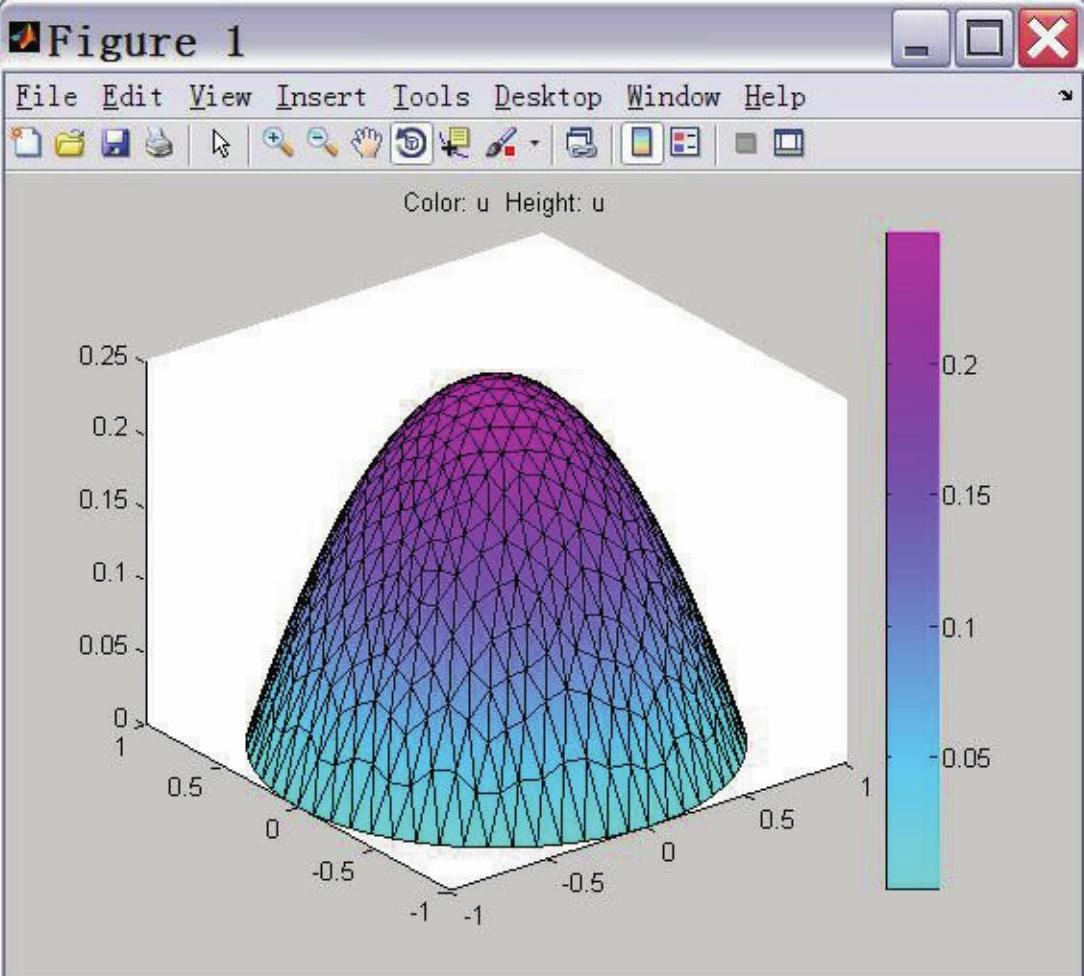
点击按钮数值求解方程，方程的数值解默认以彩色二维图显示，颜色的深浅代表函数u取值的大小。点击按钮打开画图设置对话框，勾选Color、Height(3-D plot)、Show mesh，点击Plot，得到标有剖分网格的彩色三维图，如图2-28所示。当按钮处于按下状态时，可通过鼠标左键的拖曳来旋转三维图，以调整最佳的观察角度。选择File菜单下的Save As，可将图像以指定的图片格式保存。

(www.xing528.com)

图2-28 标有剖分网格的彩色三维图

偏微分工具箱也允许用户自定义画图的内容。点击按钮打开画图设置对话框，勾选Color、Height(3-D plot)、Show mesh，并在Height(3-D plot)后面Property的下拉菜单中选择user entry，其后user entry的文本框中填入数值解与精确解的差，即u-(1-x.^2-y.^2)/4，如图2-29所示。点击Plot，得到计算误差的彩色三维图，可以看出误差在10^-4数量级，如图2-30所示。

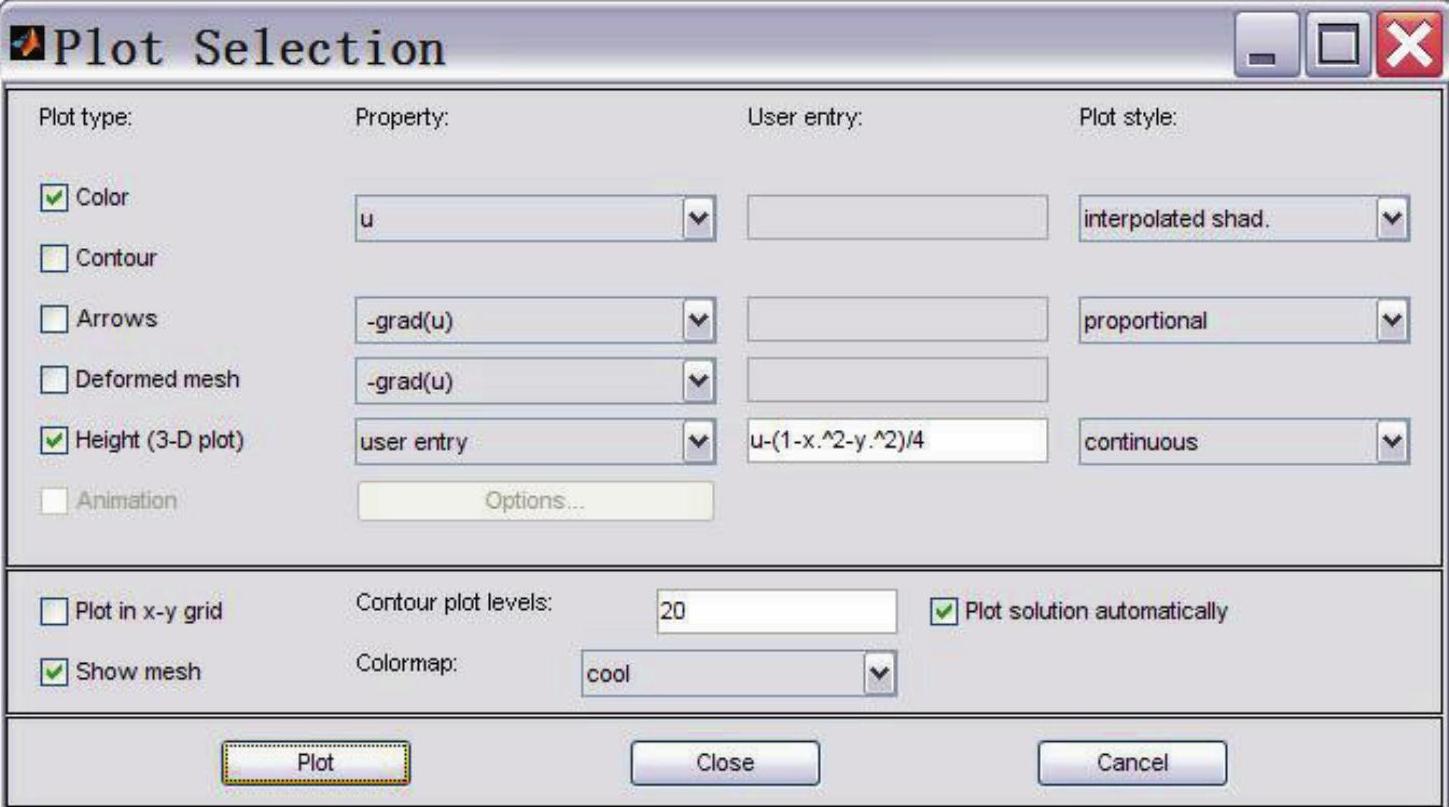
图2-29 画误差分布图的设置

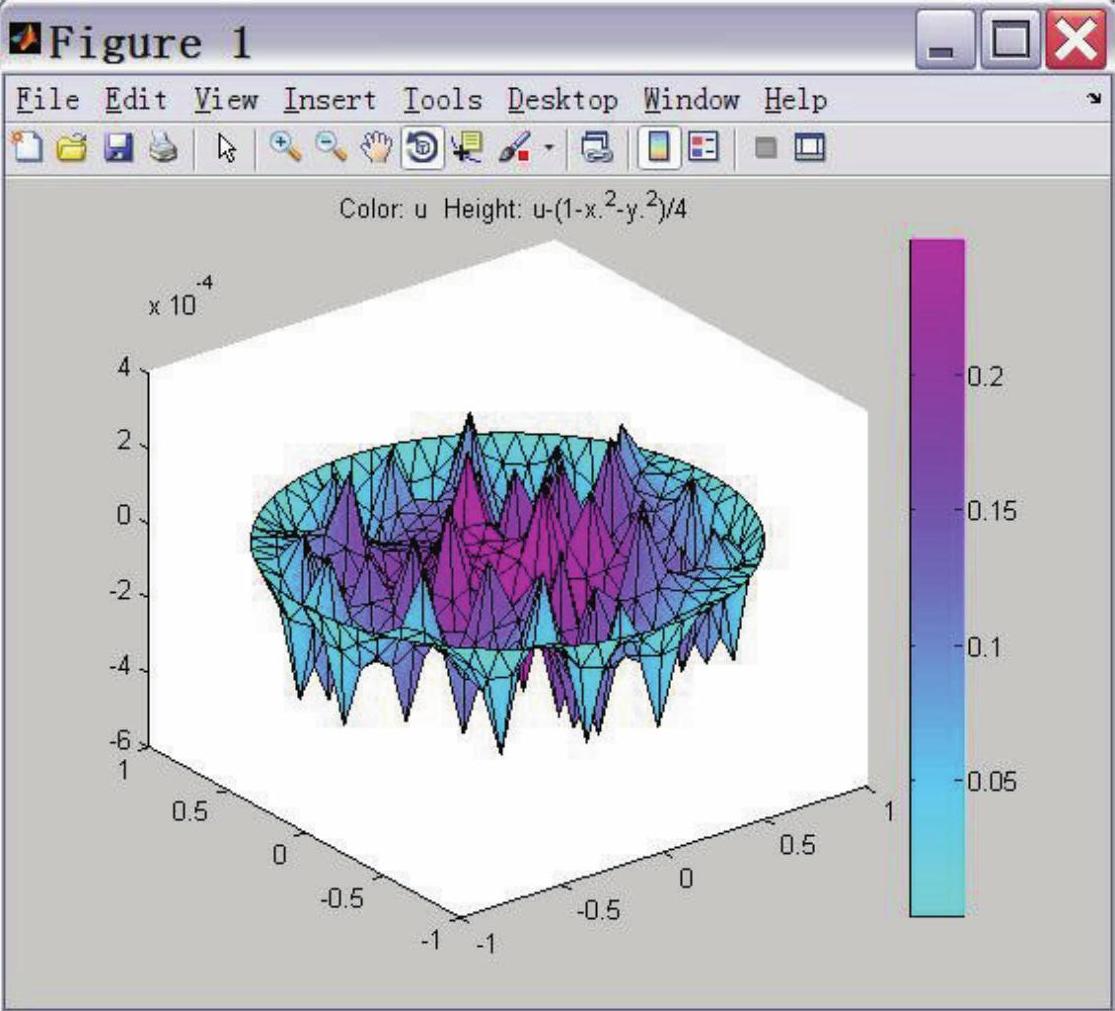
图2-30 误差的彩色三维图

要导出数值解u在每个结点处的取值，点击Solve菜单下的Export Solution选项打开导出数值解的对话框，填入导出的变量名（默认为u），点击OK即可，如图2-31所示。

图2-31 导出每个结点处的数值解

由于之前已经导出了三角网格的相关数据，所以结点位置（x、y坐标构成的二维数组，默认变量名为p，按结点序号排列）及该位置上数值解u的取值（默认变量名为u，按结点序号排列的一维数组）都出现在了workspace中，可供Matlab进行后续处理，如图2-32所示。

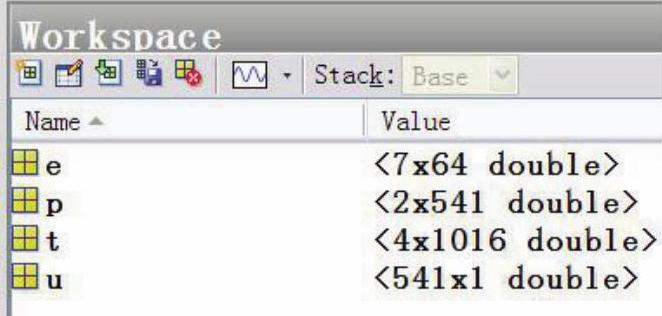
图2-32 workspace中的结点数据和对应的数值解u的取值