用Matlab高效解1维波动方程

考虑如下一维波动方程：

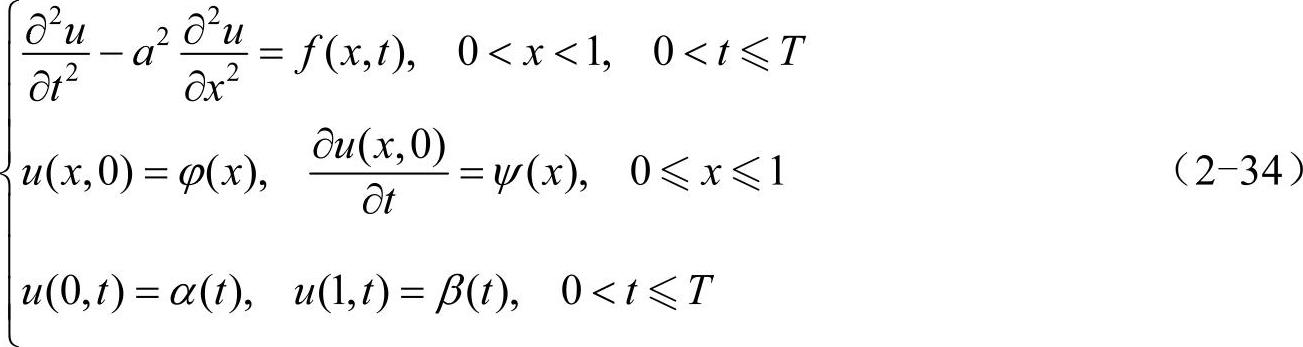
其中，a为正常数，f(x,t)、φ(x)、ψ(x)、α(t)和β(t)为已知函数。这里的计算区域网格剖分过程和2.2.2小节完全一样，就不再赘述。在结点处讨论一维波动方程，有：

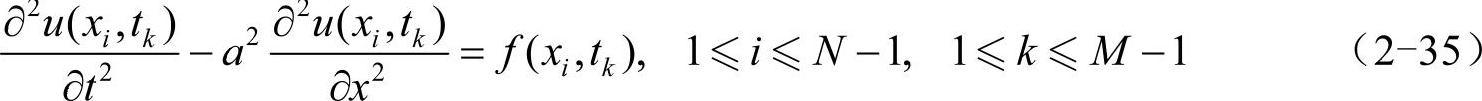
由泰勒公式，有：

将上两式代入式（2-35），并将小量O(τ²+h²)作为局部截断误差忽略掉，同时引入步长比s=aτ/h，并使用简写u^k_i=u(x_i,t_k)，得差分格式：

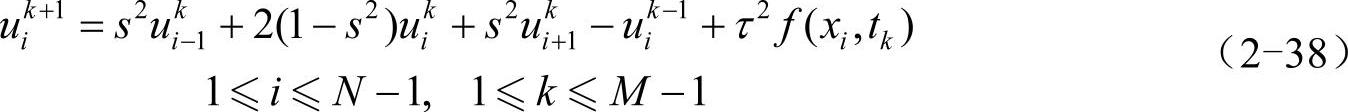
根据CFL条件，仅当步长比s≤1时，上式才是稳定的，误差也会被控制在较小的程度，证明从略。如图2-9所示为此差分格式所涉及结点的相对位置。要计算函数u在(x_i,t_k+1)处的取值，就需要用到函数u在(x_i-1,t_k)、(x_i,t_k)、(x_i+1,t_k)及(x_i,t_k-1)处的取值。

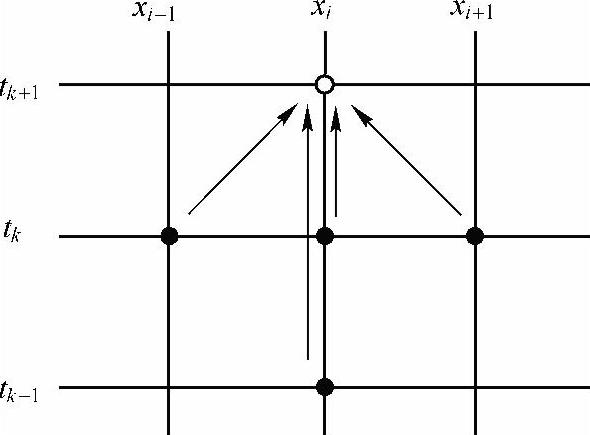
图2-9 差分格式（2-38）所涉及结点的相对位置

将差分格式（2-38）写为矩阵形式（2-39），注意最后一个向量的首尾元素已包含了边界条件：

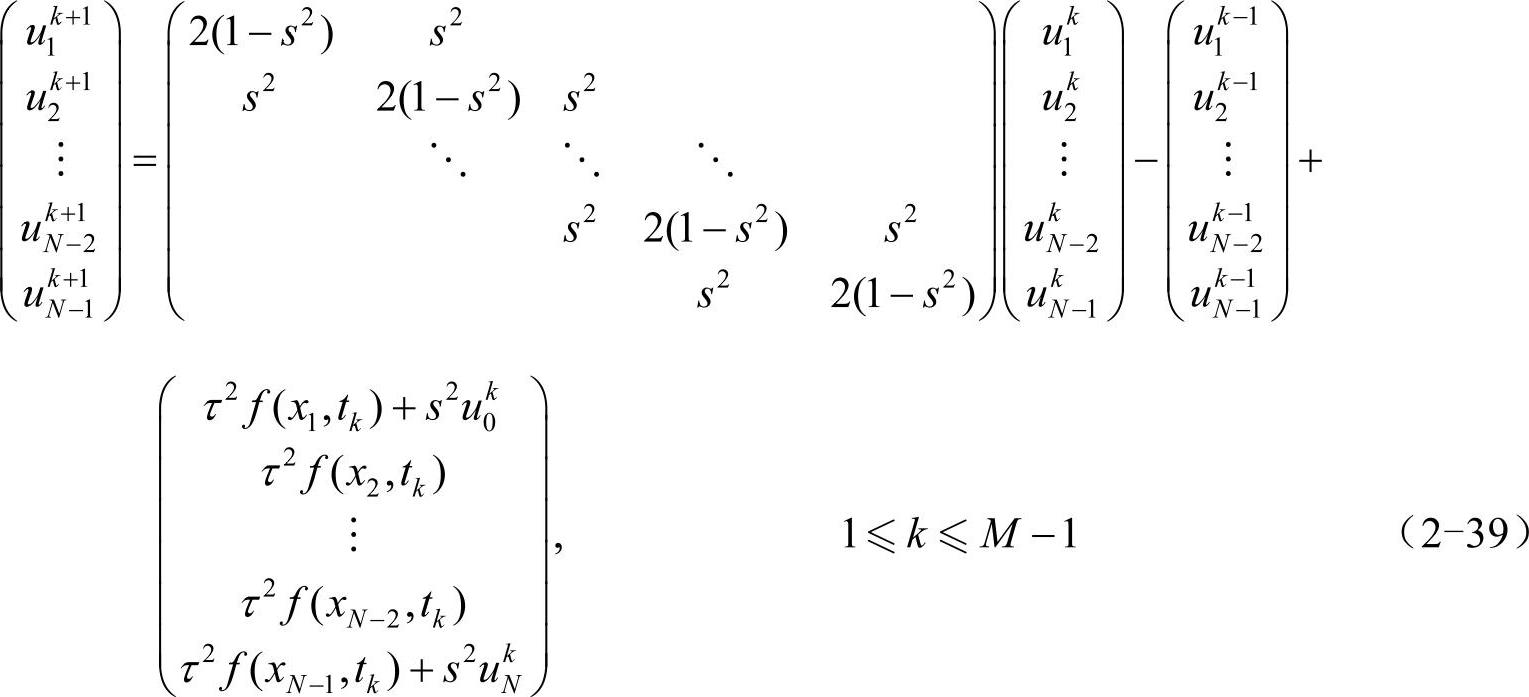(www.xing528.com)

值得一提的是，计算最开始时需要两个已知向量：(u₁⁰,u₂⁰,…,u_N-2⁰,u_N-1⁰)T和(u₁¹,u₂¹,…,uN-2¹,uN-1¹)T。第一个向量可直接通过初始条件获得，即u_i⁰=φ(x_i)，第二个向量通常选用欧拉法来近似估算，即u_i¹=φ(x_i)+τψ(x_i)。下面给出一个实例。

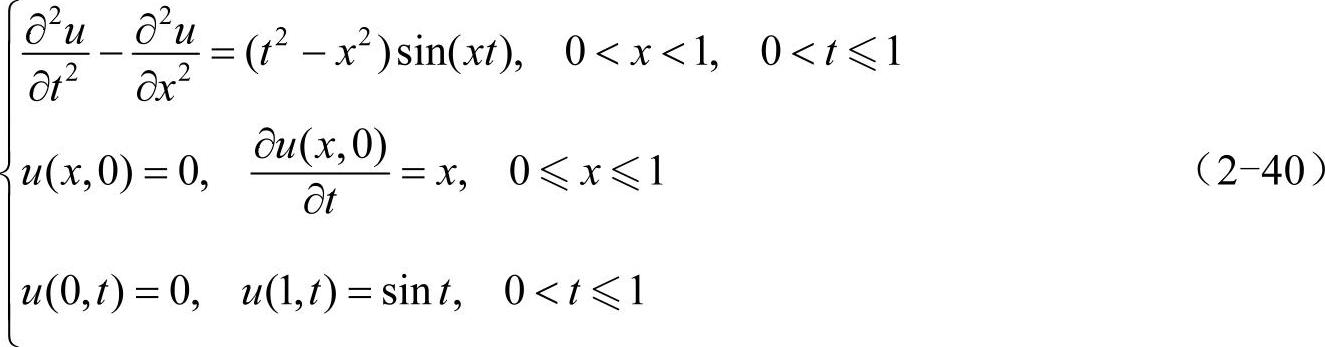
根据式（2-39）求解上式，代码如下：

程序2-4

程序输出如图2-10所示，左图为数值解，右图为数值解与解析解u=sin(xt)之间的误差。代码中的步长比s=1，此时差分格式是稳定的，误差在10^-5级。

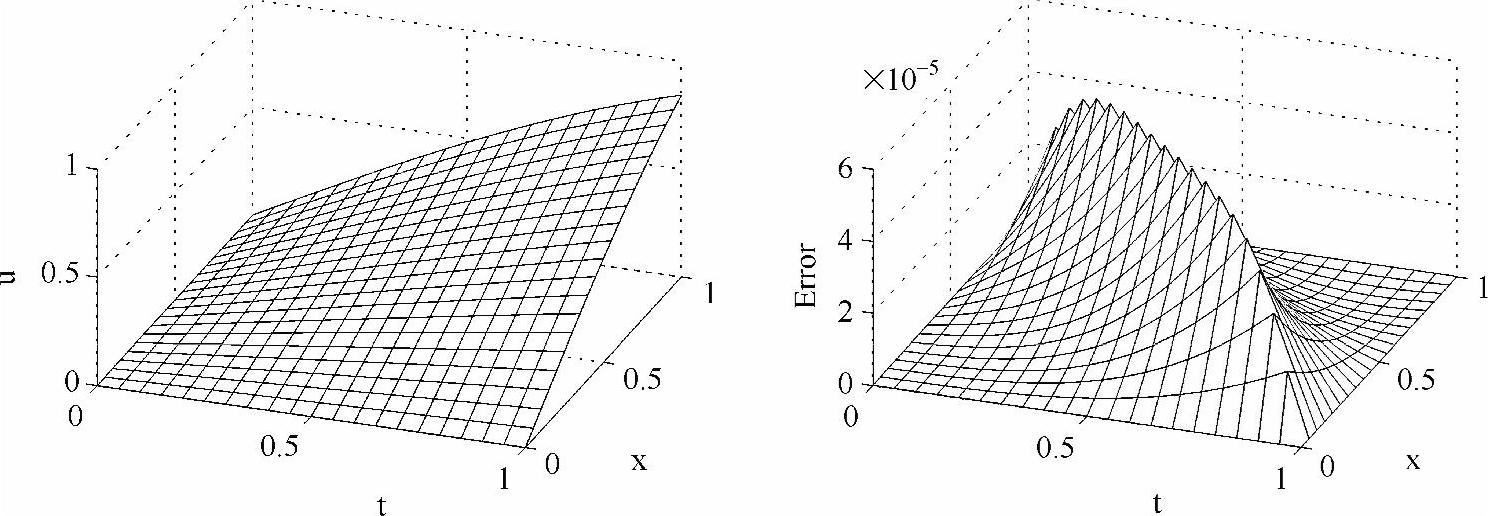
图2-10 数值结果（左图）和误差（右图）

至此，针对三种常见偏微分方程的有限差分法原理和示例就介绍完了。实际上，有限差分法还有更多深入的内容，限于篇幅没有在此处提及。简单来讲，有限差分法的核心思路就是通过差商来近似偏微分方程中的偏导数（如：∂u/∂t、∂²u/∂t²、∂²u/∂x²），得到可直接迭代计算的差分格式，进而数值求解。这在过去几十年间都是处理偏微分问题的基本有效手段。

但是，有限差分法是一种局部的方法，即每个位置的导数（∂u/∂x、∂²u/∂x²……）都是由临近的几个点计算而来的。计算过程中所使用的矩阵都是包含很多0的稀疏矩阵也反映了这一点，因此它的精度不高。而后续章节即将讨论的谱方法是全局的算法，它使用所有已知点来计算某一处的导数，这样就大大提高了精度。

另外，在包含时间的偏微分问题中，由于CFL条件的限制，有限差分法不能采用较大的时间步长快速地得到结果。而在后文中，利用谱方法求解此类问题时，将使用变步长的ode系列函数计算∂u/∂t，无需选定固定的时间步长就能在较高精度的前提下尽快得到结果。