Matlab高效解谱法：二维泊松方程

考虑区域Ω上的二维泊松问题：

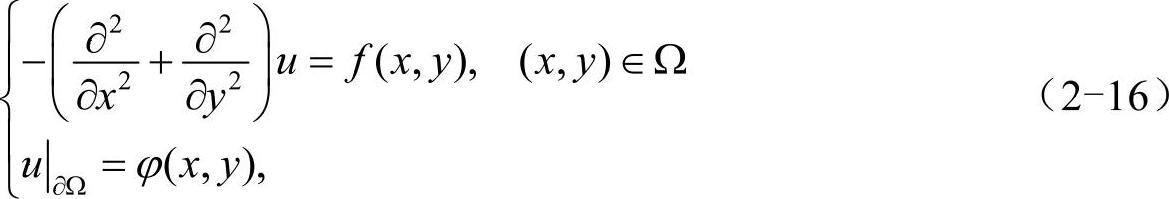
其中，∂Ω为区域Ω的边界，f(x,y)和φ(x,y)为已知函数。u|∂Ω=φ(x,y)描述了函数u在边界上的取值，即所谓的边界条件。为简单起见，这里仅讨论Ω为矩形的情况，即a＜x＜b，c＜y＜d。首先，用间隔h₁=(b-a)/N、h₂=(d-c)/M分别将x轴上的区间[a,b]、y轴上的区间[c,d]划分为N、M等分，得x_i=a+ih₁、0≤i≤N和y_j=c+jh₂、0≤j≤M。再根据x_i和y_j对矩形区域进行网格剖分，如图2-3所示。横线与竖线的交点就是网格结点，称位于边界∂Ω上的结点为边界结点，其余结点为内结点。

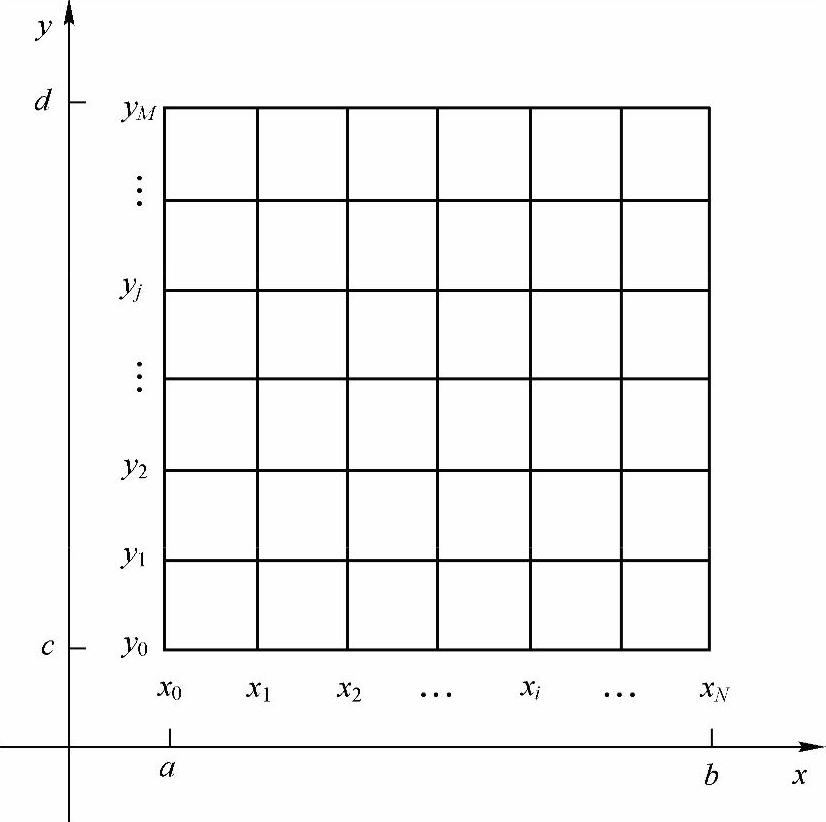
图2-3 矩形区域的网格剖分

在内结点处考虑泊松问题：

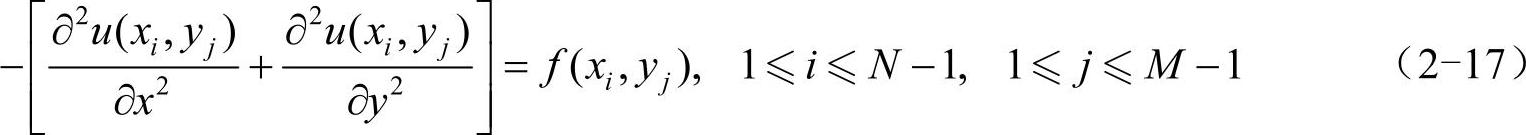
由泰勒公式，有：

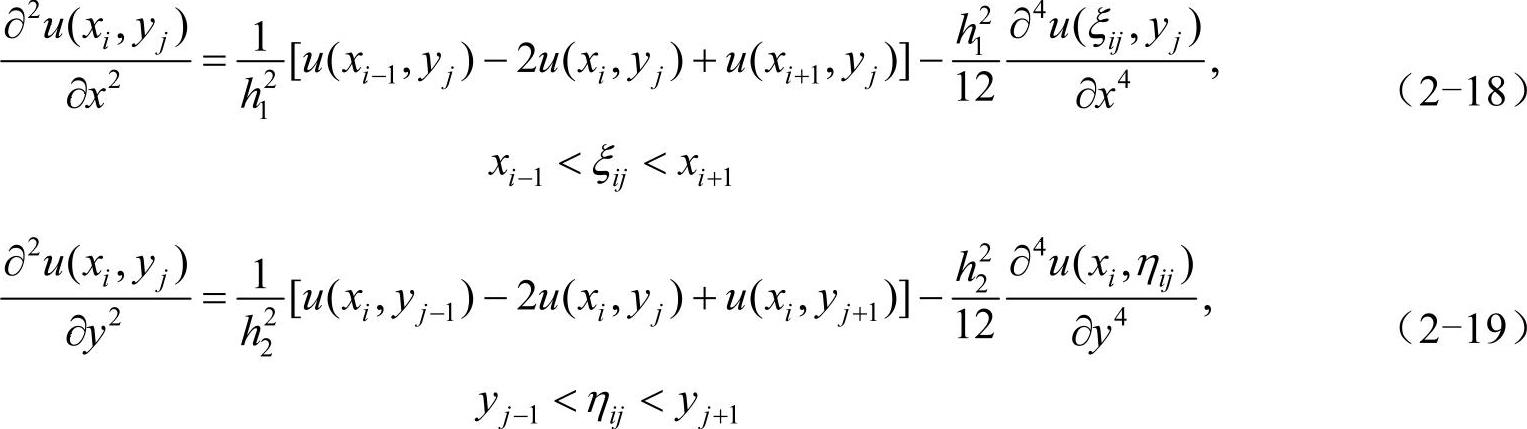
将以上两式代入式（2-17），忽略小量O(h²₁+h²₂)，并使用简写u_ij=u(x_i,y_j)，得到差分格式（2-20）。所谓差分格式，就是用几个相邻数值点的差商来替代方程中的导数或偏导数的近似算法。

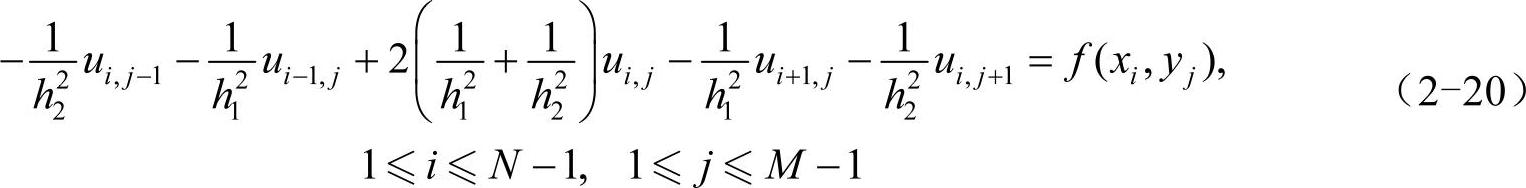
先定义向量u_j：

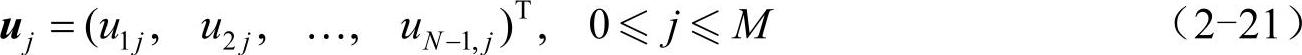
再将差分格式（2-20）写为矩阵形式：

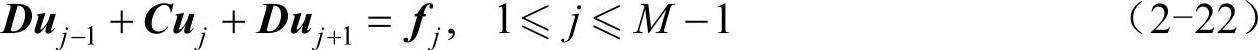
其中，矩阵C、D、向量f_j的定义如下，注意向量f_j的首尾元素已包含了x=a和x=b处的边界条件。(www.xing528.com)

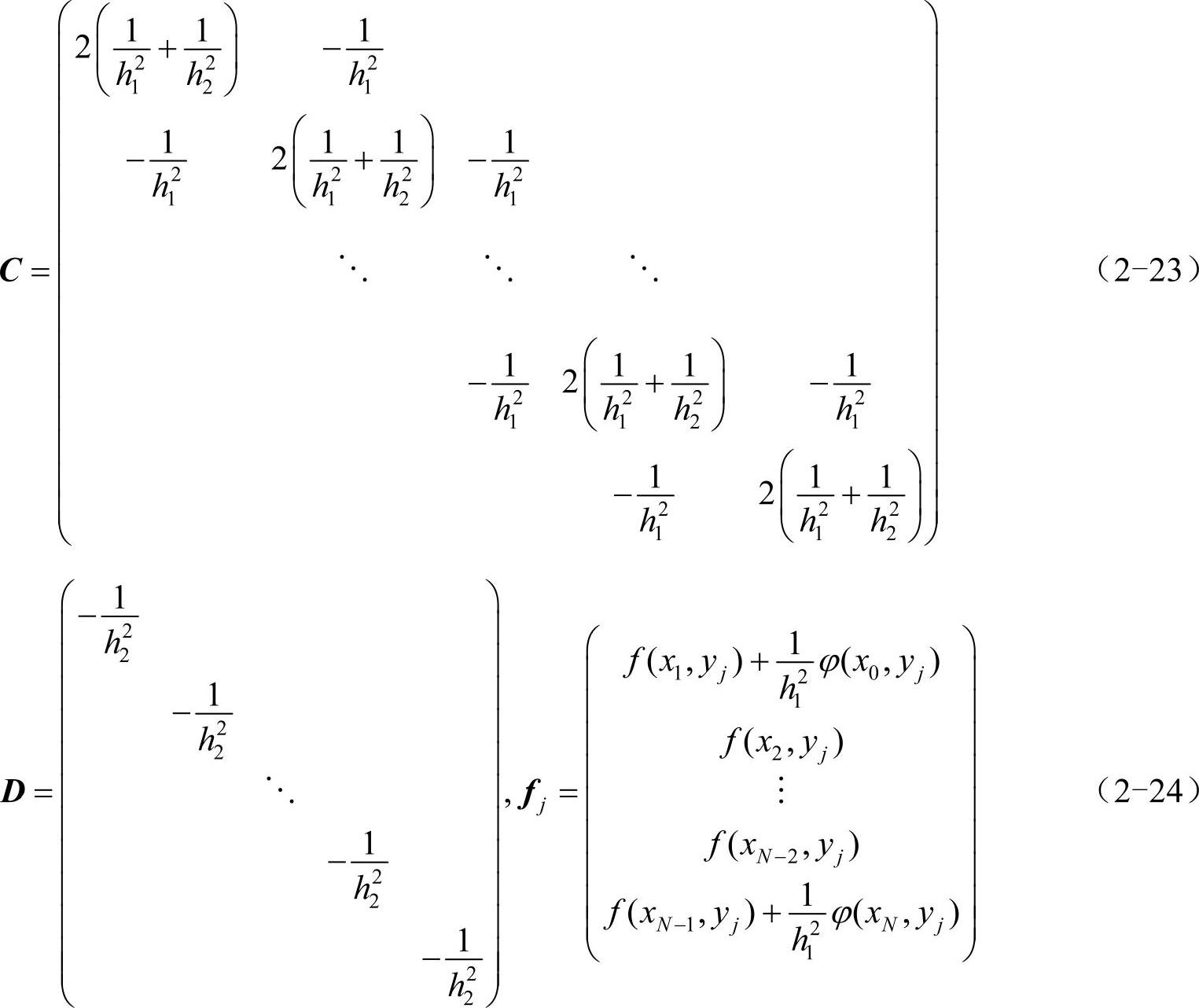
式（2-22）还可以进一步写成如下的矩阵形式，注意等号右边向量的首尾元素加入了y=c和y=d处的边界条件。

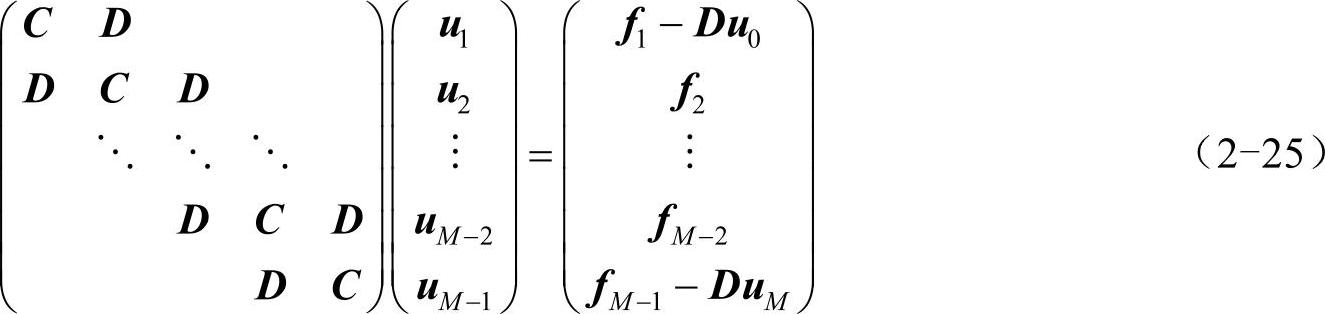
因此，矩形Ω上的二维泊松问题就转化为上面形如Au=f的矩阵问题。对于这类问题，最直接的解法就是先求A的逆矩阵A-1，然后u=A-1f即可，这在Matlab中可用左除“\”实现。注意式（2-22）只针对内结点，所以C、D均是N-1阶方阵，A是(N-1)(M-1)阶方阵。下面给出一个实际例子。

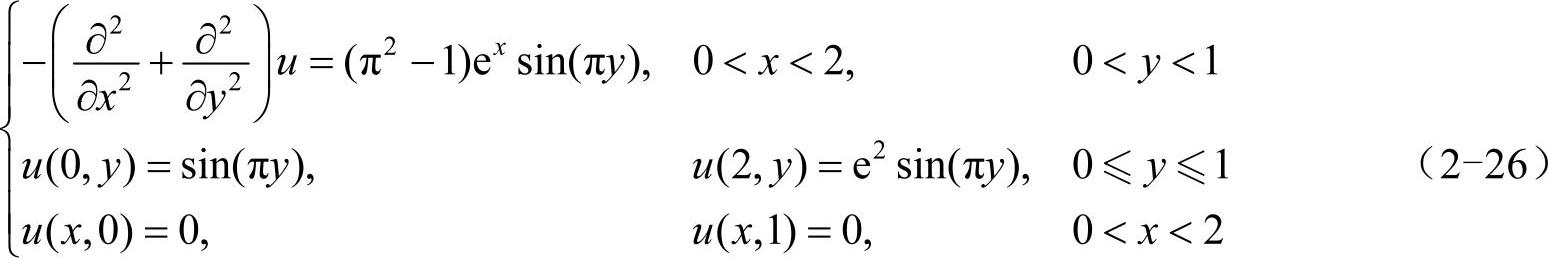
根据式（2-25）求解这个泊松问题，代码如下：

程序2-2

程序输出结果如图2-4所示，左图为h₁=h₂=0.1时泊松问题（2-26）的数值解，右图为数值解与解析解u=e^xsin(πy)之间的误差。当然，进一步缩小h₁和h₂会以增加运算量为代价降低这个误差。

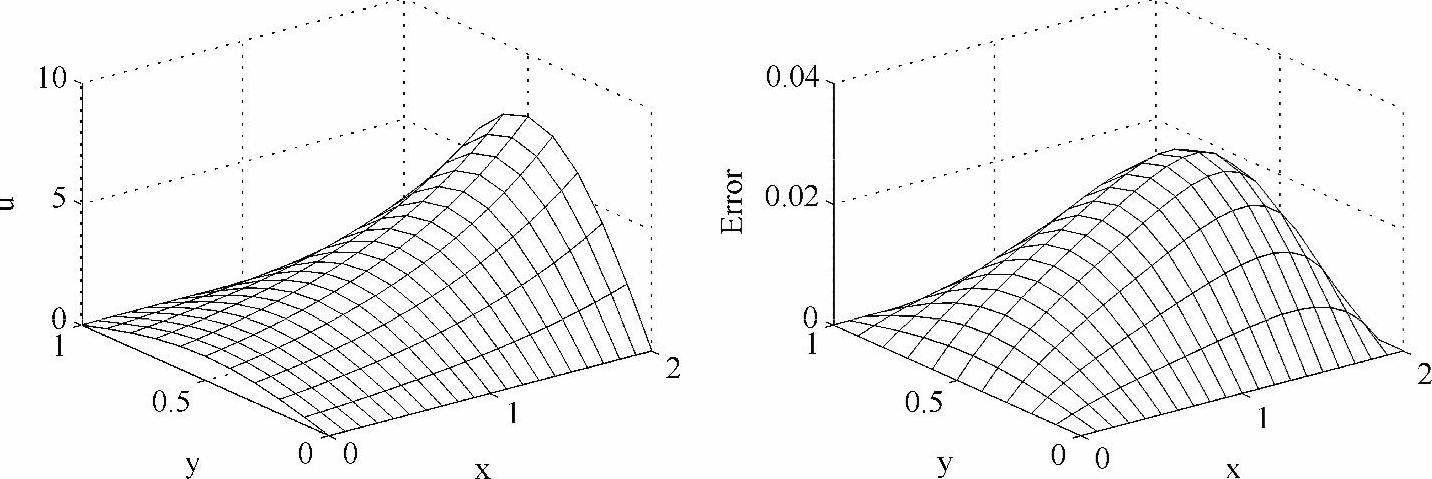
图2-4 数值结果（左图）和误差（右图）

为了使读者产生直观的理解，图2-5显示了h₁=h₂=0.2时方阵A的非零元素分布情况。

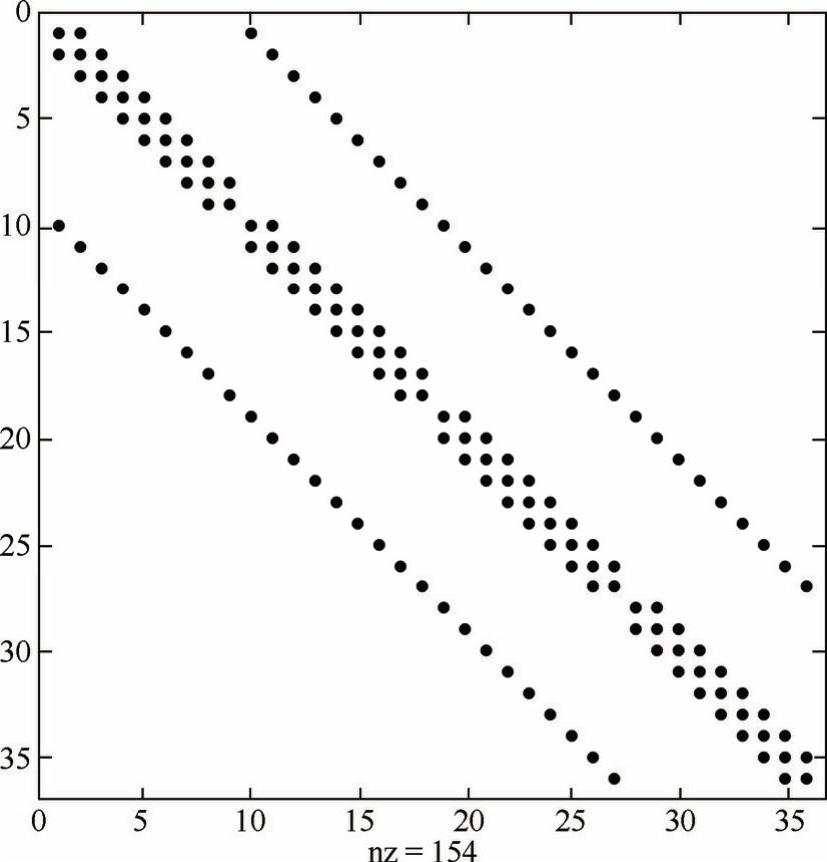
图2-5 方阵A的非零元素分布