【摘要】：众所周知，Matlab在矩阵运算方面的速度比较快，而且矩阵形式的代码也更加简洁明了，所以接下来将数值微分写成矩阵的形式。程序2-1图2-21 阶向前差商、1阶中心差商、2阶中心差商的结果（点）与解析解（曲线）
2.1.1小节给出了数值微分的原理及公式，要在Matlab中实现这样的数值微分，既可以用循环语句，也可以用矩阵乘法的形式。众所周知，Matlab在矩阵运算方面的速度比较快，而且矩阵形式的代码也更加简洁明了，所以接下来将数值微分写成矩阵的形式。
（1）若u(x)为周期函数且周期为b-a+h。
1阶导数的向前差商公式可写为：
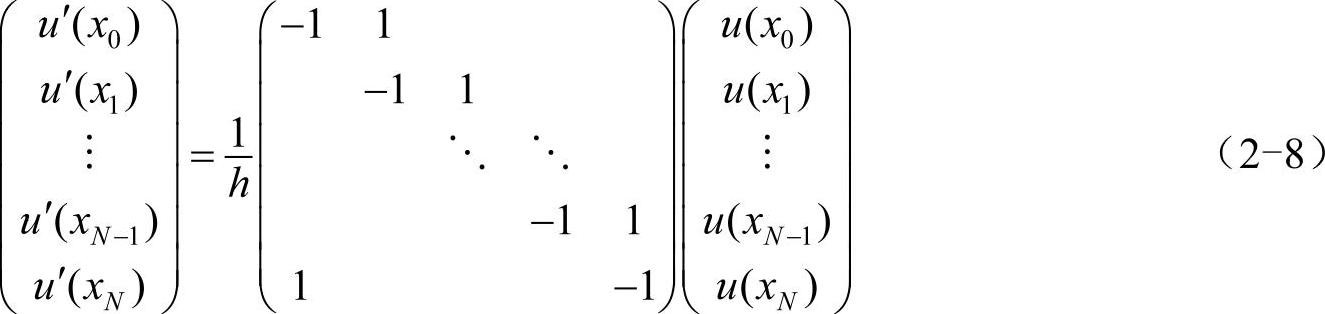
1阶导数的向后差商公式可写为：
1阶导数的中心差商公式可写为：
2阶导数的中心差商公式可写为：
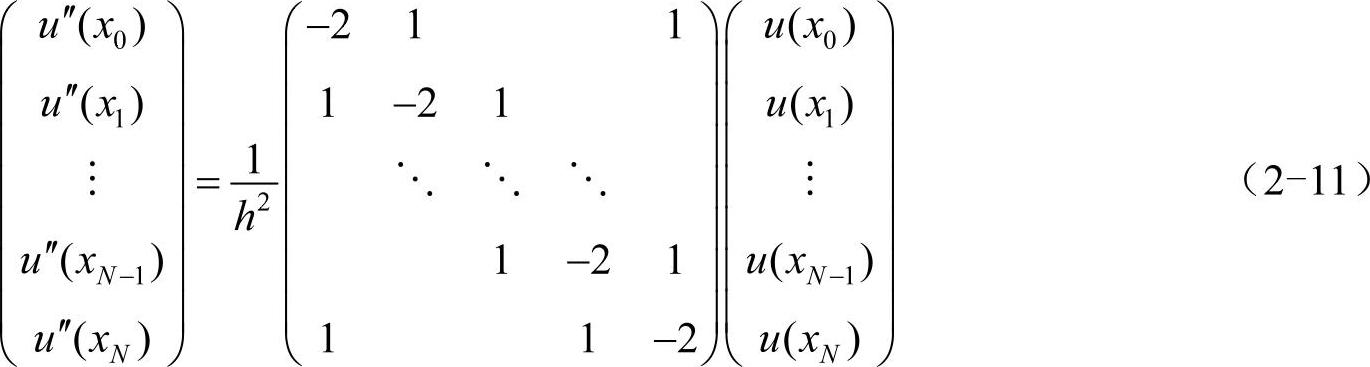
（2）若有条件给出u(x0-h)和（或）u(xN+h)的值。
1阶导数的向前差商公式可写为：
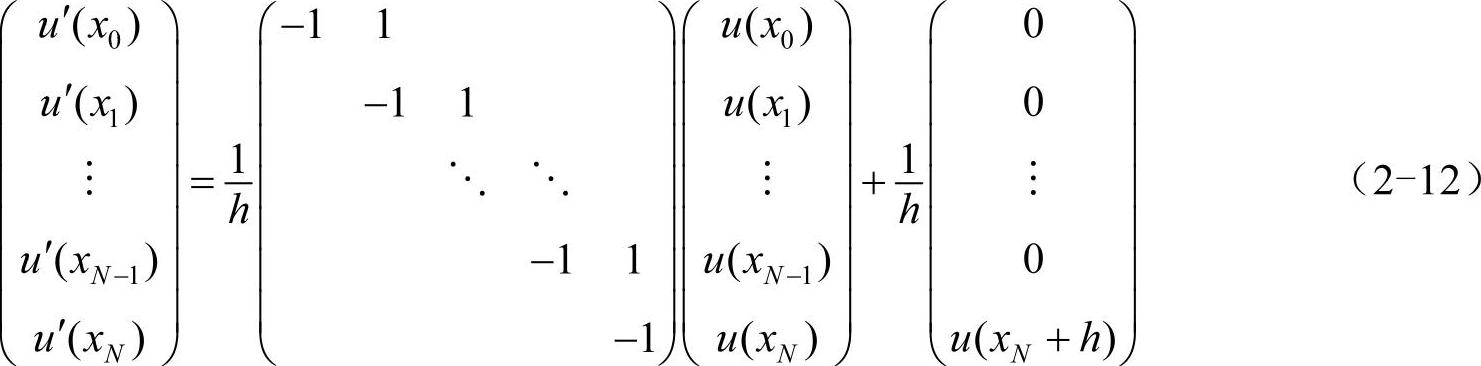(www.xing528.com)
1阶导数的向后差商公式可写为：
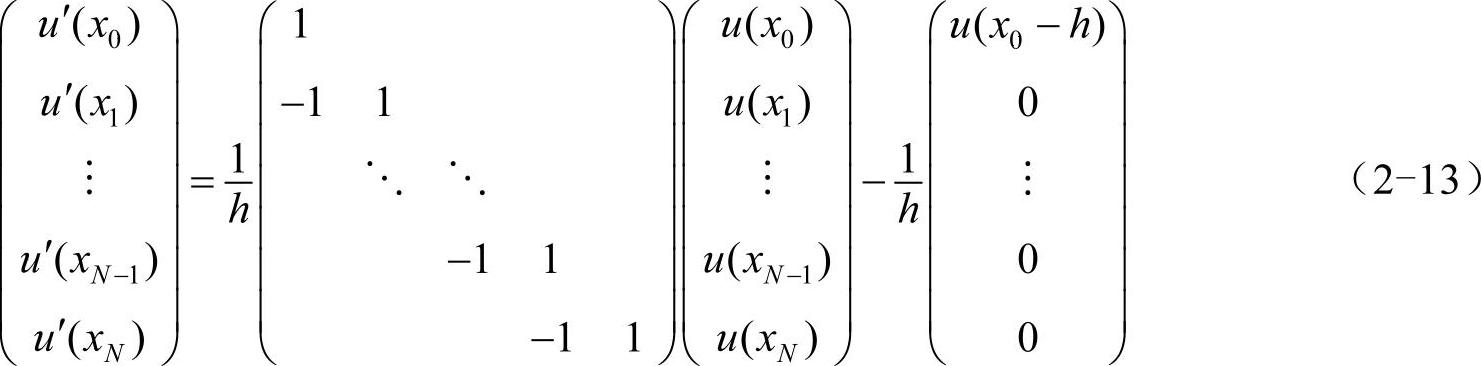
1阶导数的中心差商公式可写为：
2阶导数的中心差商公式可写为：
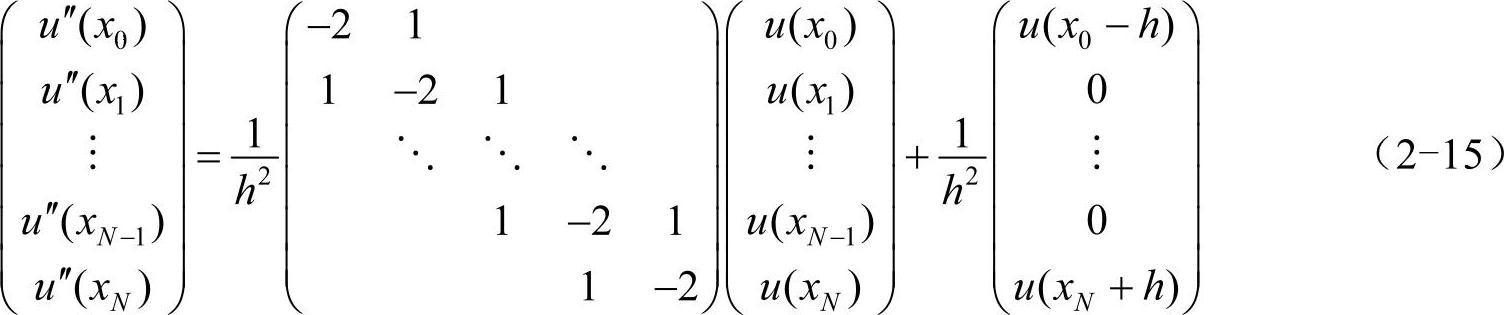
下面用实例说明周期函数u(x)=esin(πx)的1阶、2阶导数的数值计算过程，并且与相应的解析解u'(x)=πcos(πx)esin(πx)、u"(x)=π2esin(πx)[cos2(πx)sin(πx)]做比较，代码如下。程序输出结果如图2-2所示，误差最大的是1阶导数的向前差商公式，而1阶、2阶导数的中心差商公式则更精确，这是由局部截断误差决定的。
程序2-1
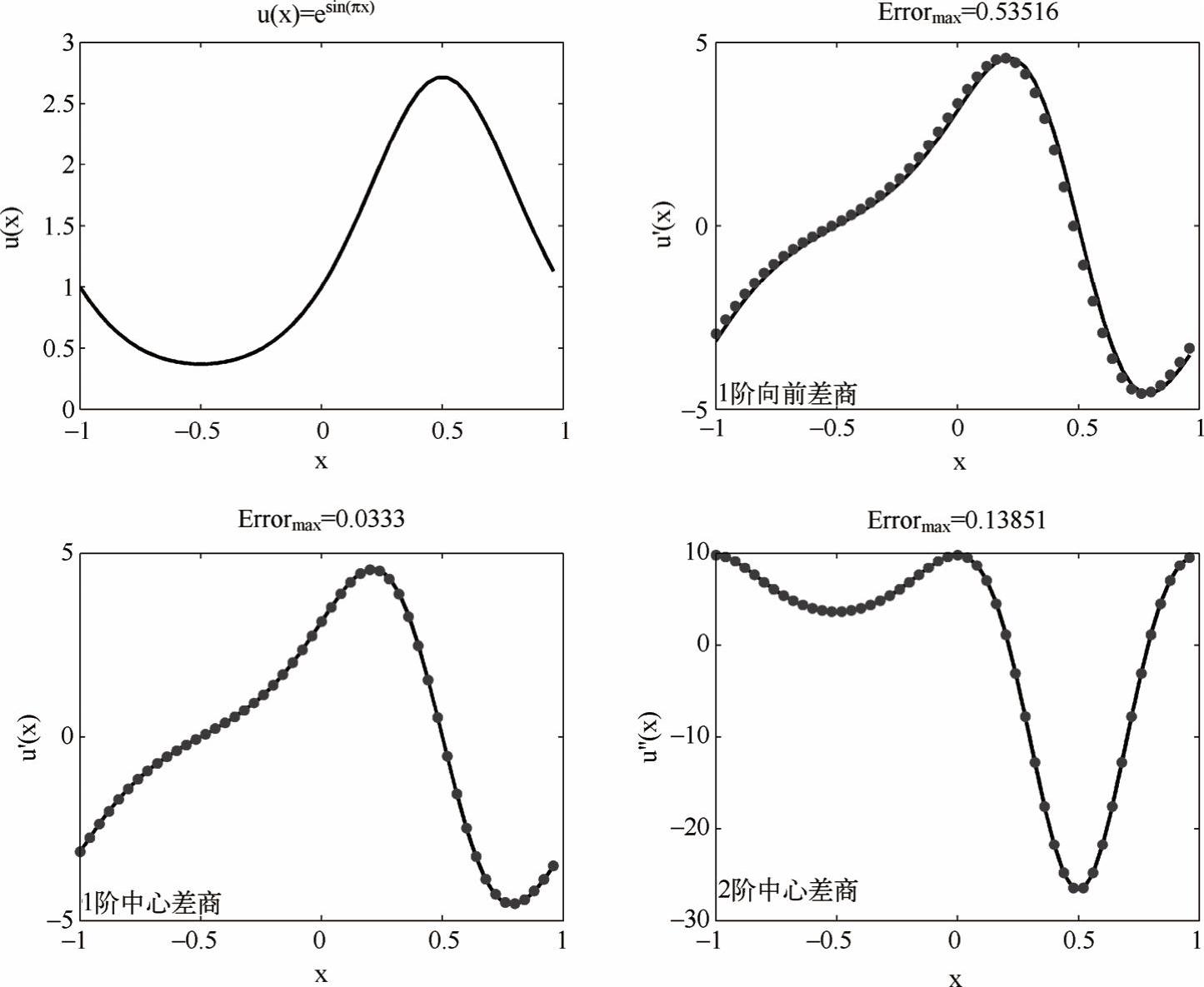
图2-21 阶向前差商、1阶中心差商、2阶中心差商的结果（点）与解析解（曲线）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
