Matlab微分方程高效解法：bvp系列函数的用法

与专门针对初值问题的ode系列函数类似，Matlab中还有专门用于解决边值问题的bvp系列函数，其调用语法为：

sol=bvpsolver(odefun,bcfun,solinit,options)

下面对每一项进行说明：

（1）“bvpsolver”是bvp系列函数的名称，可以是bvp4c或bvp5c，后者比前者的精度高一些。

（2）“odefun”是包含常微分方程组的函数句柄，这与ode系列函数中的odefun是一样的。

（3）“bcfun”是包含边界条件的函数句柄。

（4）“solinit”是包含初始网格结点、初始猜测值的结构体，由bvpinit函数生成。

（5）“options”用于改变bvpsolver的默认设置，由bvpset函数生成，为可选项。

（6）“sol”为包含计算结果的结构体。

如不需要用到options，则bvp系列函数的调用形式为：

sol=bvpsolver(odefun,bcfun,solinit)

用于生成结构体solinit的bvpinit函数的调用语法为：

solinit=bvpinit(x,uinit,params)

其中：

（1）“x”为计算区间内的初始网格结点，起止点即为边界条件所在的两处位置，这些结点需要按大小单调排列。

（2）“uinit”是解的初始猜测值，也可以是每个结点处的解的猜测值。

（3）“params”是边值问题中的未知参数（如果有的话）的猜测值，为可选项。(www.xing528.com)

下面举例说明bvp4c的用法，边值问题如下：

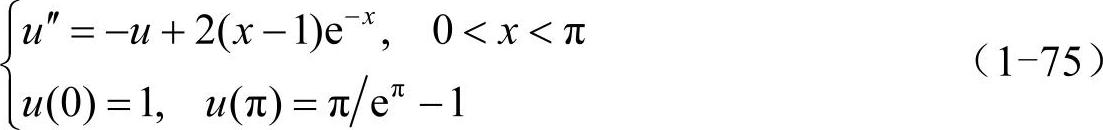
先利用代换u₁=u、u₂=u′，化为一阶常微分方程组形式：

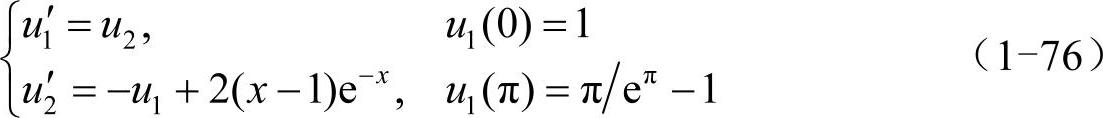
将此常微分方程组和边界条件分别写进shoot2.m和bc.m中，用bvp4c求解，代码如下：

程序1-5

主程序代码如下：

文件shoot2.m代码如下：

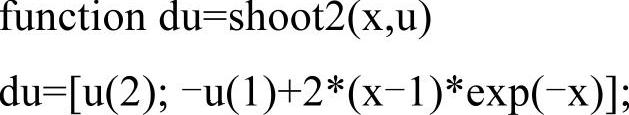
文件bc.m代码如下：

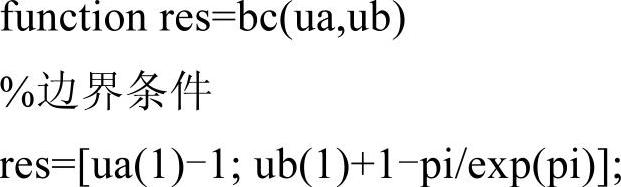
这里重点说明一下包含边界条件的文件bc.m，其中定义了一个同名函数bc，参数ua和ub分别代表左边界和右边界的情况。其中，ua(1)和ua(2)为函数在左边界的取值和一阶导数，ub(1)和ub(2)为函数在右边界的取值和一阶导数。代码中的“ua(1)-1”就是ua(1)-1=0的简写，代表边界条件u(0)=1，同理，“ub(1)+1-pi/exp(pi)”表示u(π)=π/eπ-1。

代码中的初始猜测值为u₁=2、u₂=2，假如边值问题的解是唯一的，初始猜测值的选取是不会影响结果的。图1-8同时显示了bvp4c得到的数值解和式（1-75）的解析解u=cos(x)+xe^-x，二者相当吻合。值得一提的是，如果在bvpinit函数中选取的初始网格结点数量偏少的话，会造成数值解和解析解存在一定的差异，在这一点上，bvp4c比打靶法更难使用。

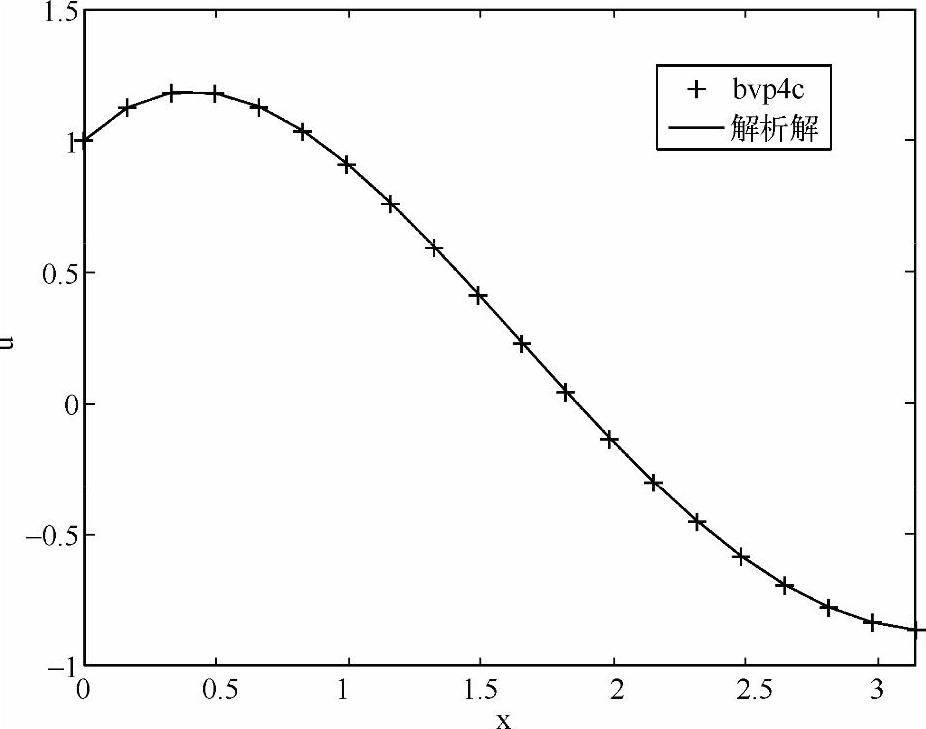
图1-8 边值问题的数值解与解析解