Matlab微分方程高效解法：打靶法实现及结果

对于二阶常微分方程（1-65）及边界条件（1-67），利用代换u₁=u、u₂=u′，可将其写为等价的方程组形式：

它与初值问题的不同之处在于，u₂(a)的值是未知的，已知条件中取而代之的是u₁(b)的值，否则就可以直接通过odesolver数值求解了。假如可以确定一个值m，使初值问题（1-69）的解u₁(x)满足|u₁(b)-β|＜ε,其中ε为可允许的误差，那么边值问题（1-68）和初值问题（1-69）的解就是近似相等的，也就相当于把边值问题转化成了初值问题。

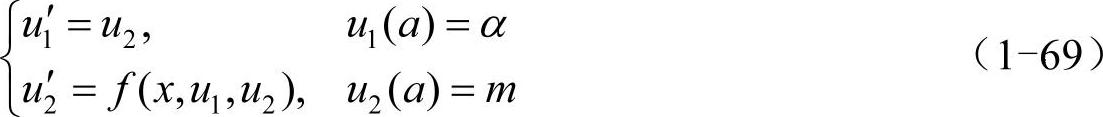
打靶法就是用来确定m值的，大致思路如下：

（1）随意选取m的起始值。

（2）求出初值问题（1-69）的解u₁(x)。

（3）若不符合|u₁(b)-β|＜ε，就修正m的值。

（4）重复前面两项，直到符合|u₁(b)-β|＜ε，此时的u₁(x)就是数值解。

修正m取值的方法可以是线性插值法、牛顿法等，这里使用比较简单的线性插值法。设m=m_n时初值问题（1-69）的解u₁(x)在x=b处有u₁(b)=β_n，其中n=1,2,…。若假设m_n与β_n是线性关系，为了让m取最新修正值m_n+2时有β_n+2=β，则m_n+2需要满足(m_n+2-m_n)/(β-β_n)=(m_n+1-m_n)/(β_n+1-β_n)，即：

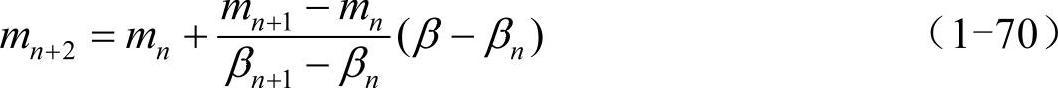
其中的m_n、β_n、m_n+1、β_n+1为已知，这就是说如果使用线性插值法修正m的取值，在打靶法开始时需要先随意选取2个m的起始值m₁、m₂，计算出相应的β₁、β₂，才可以根据上式得到修正值m₃，进而得到β₃，然后得到修正值m₄……直到找到满足|β_n-β|＜ε的m值。此时初值问题（1-69）的解即近似为边值问题（1-68）的解，而初值问题是容易数值求解的。

打靶法的过程如图1-5所示，虽然m取m₁、m₂时，最终结果在x=b处的取值与应有的边界条件相差甚远，但通过一次一次地修正，逐渐缩小距离目标的差距，最终总会得到在一定误差内满足x=b处边界条件的解。

对于更复杂的边界条件（1-66），照样可以用打靶法解决。尽管u(a)和u′(a)的值都是未知的，但只要猜测它们其中一个的取值，就可以通过关系α₁u(a)+β1u′(a)=γ₁得到另外一个的值。有了u(a)和u′(a)的值，再通过odesolver求解式（1-65）得到u(b)和u′(b)的值（当然需要变量代换u₁=u、u₂=u′），然后使用|α₂u(b)+β2u′(b)-γ₂|＜ε判断猜测的初始值是否符合要求，如失败就修正猜测值后继续尝试，直到符合要求。这样一来，同样可以将边界条件（1-66）下的边值问题当做初值问题处理。

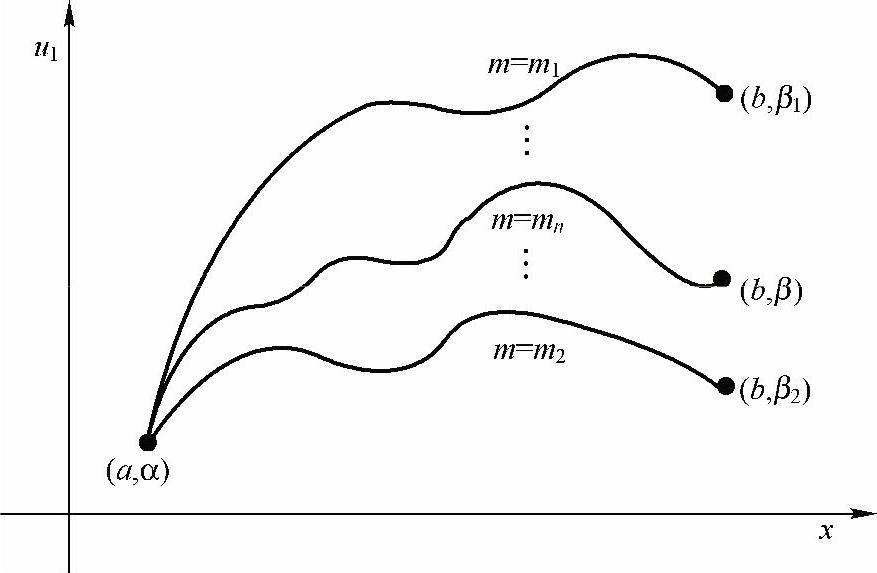
图1-5 打靶法示意图

下面举一个例子，考虑如下二阶常微分方程：

u′′+|u|=0,0＜x＜4 （1-71）

其边界条件为：(www.xing528.com)

u(0)=0,u(4)=-2 （1-72）

做代换u₁=u、u₂=u′，写为一阶常微分方程组形式：

将此问题转化为初值问题，就需要找到一个m=m_n，使式（1-74）的解u₁(x)在x=4处的值u₁(4)=βn满足|βn+2|＜10-6。

根据打靶法思想，确定m取值的流程如图1-6所示，相应代码如下：

程序1-4

主程序代码如下：

文件shoot.m代码如下：

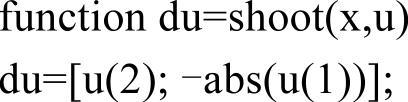
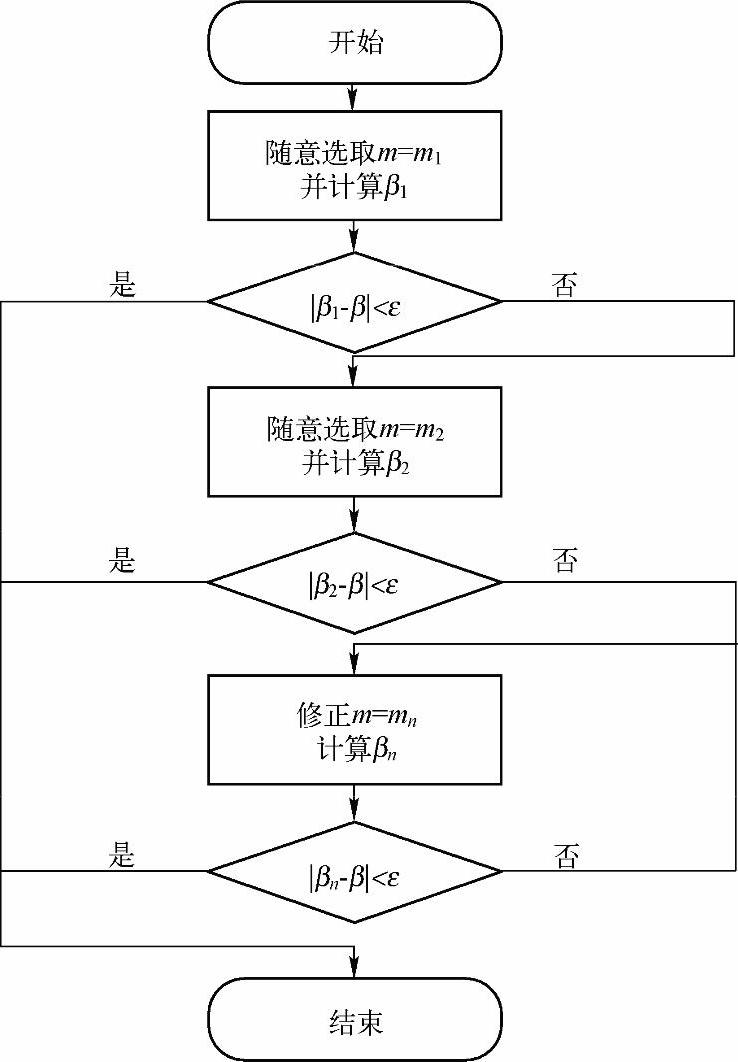
图1-6 打靶法流程图

代码中使用的m的前两个猜测值为1和0.9，程序仅经过了5次循环，就满足条件|β5⁺²|＜10^-6，得到结果如图1-7所示。如选取m的前两个猜测值为-1和-1.1，还会得到另外一个截然不同的解。因为边值问题的解往往不是唯一的，所求得的解与猜测值的选取有关，这是边值问题与初值问题的一个很大不同。

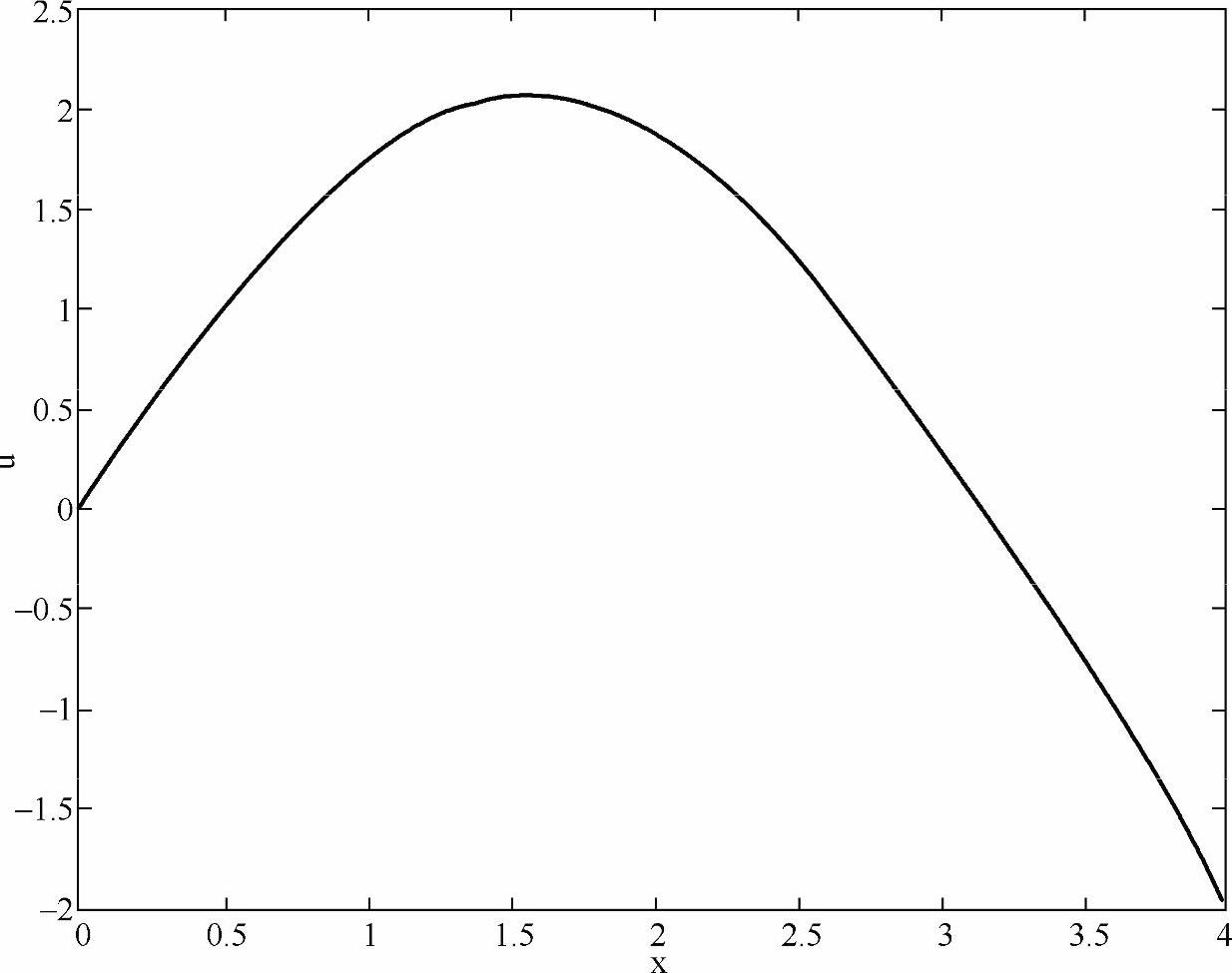
图1-7 边值问题的解

查看程序运行后m_n和β_n的前5个值，可发现线性插值法的修正效率还比较令人满意。