龙格-库塔法的高效解法

将欧拉法写成式（1-37）的形式，可以看出它实际上利用了f(x,u)在x_n处的取值来计算u_n+1的值。类似地，隐式欧拉法使用了f(x,u)在x_n+1处的近似值来计算u_n+1的值，而欧拉法和隐式欧拉法的精度都是1阶。

同样，将预测-校正法写成如下形式，不难发现它其实是用f(x,u)在x_n和x_n+1两处的取值来计算u_n+1的值，并达到了2阶的精度。

上述方法都是通过f(x,u)在不同位置的线性组合来计算u_n+1的值，所考虑的位置越多，精度也就越高。顺着这样的思路想下去，如果用f(x,u)在更多位置的线性组合来构造递推公式，将会得到更高的精度，这就是龙格-库塔法（Runge­Kutta method）的思想。这样，递推公式将有如下形式：

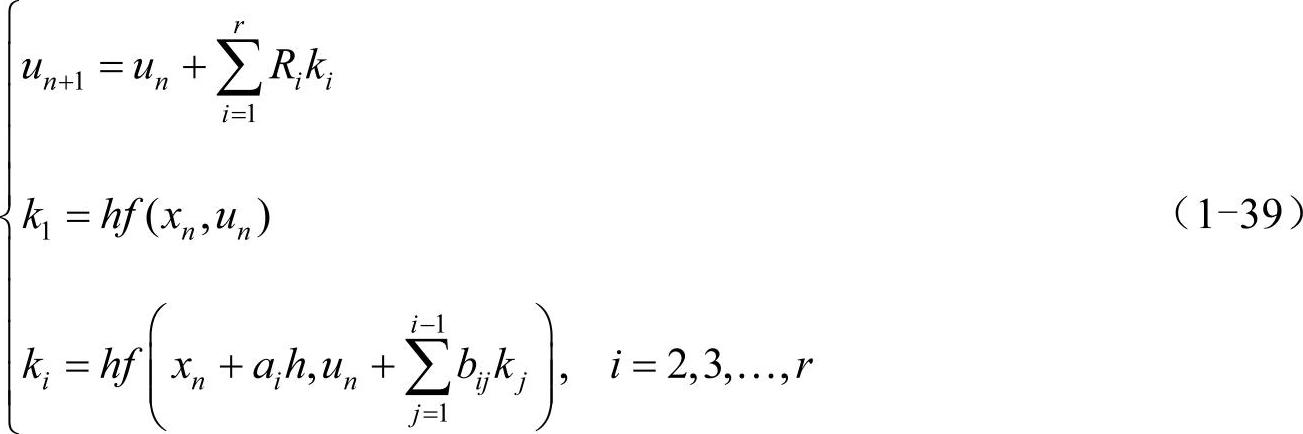
其中，R_i、a_i、b_ij为待定常数。由于使用了f(x,u)在r个位置的取值，称递推公式（1-39）为r阶龙格-库塔法。为了确定其在某一精度下的待定系数，需要将式中的u_n+1在x_n处泰勒展开，并与u(x_n+1)在x_n处的泰勒展开式比较：

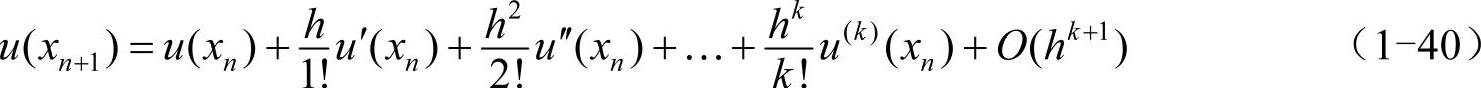
若待定常数R_i、a_i、b_ij的取值使得两式最多有前k+1项相同，那么：

u(x_n+1)-u_n+1=O(h^k+1) （1-41）

这即是说，此时R_i、a_i、b_ij的取值使得式（1-39）具有k阶的精度，下面举例说明。

当r=2时，龙格-库塔法递推公式为：

将k₂的表达式在x_n处展开：

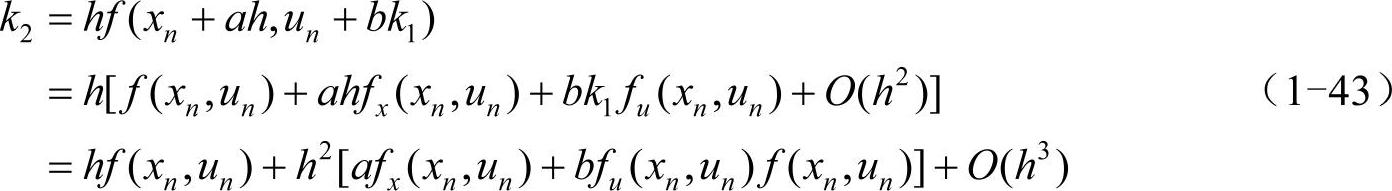
将k₁和k₂代入u_n+1的表达式：

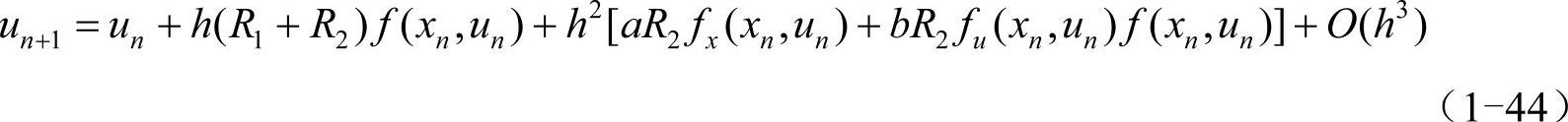
假设u_n=u(x_n)，并根据式（1-1）中的第1个式子，使式（1-40）和式（1-44）的前3项相同，得到：

(www.xing528.com)

满足上式的R₁、R₂、a、b可以有无穷多种情况，每种情况的局部截断误差都是O(h³)，都被称为二阶龙格-库塔法。如果取R₁=R₂=1/2、a=b=1，就是前面提到的预测-校正法。如果取R₁=0、R₂=1、a=b=1/2，就得到中点公式（midpoint method）：

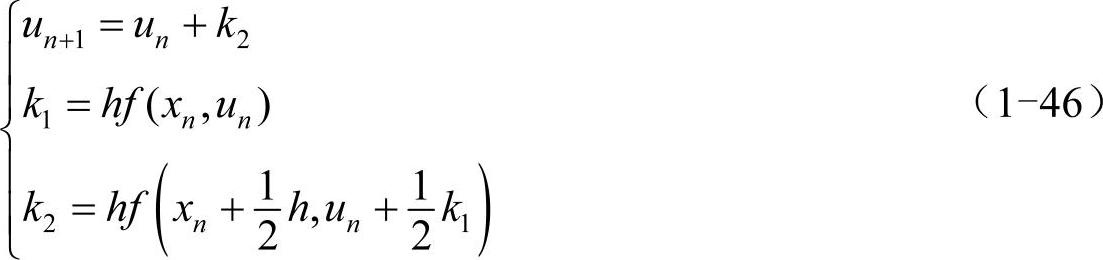
二阶龙格-库塔法不能保证局部截断误差为O(h⁴)，所以接下来考虑r=3的情况，即：

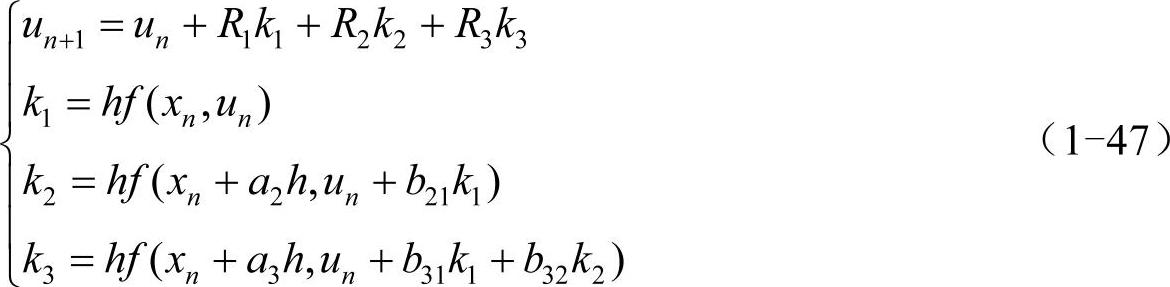
与r=2的情况类似，先写出上式中的u_n+1在x_n处的泰勒展开式，并假设u_n=u(x_n)，与式（1-40）比较，要保证局部截断误差为u(x_n+1)-u_n+1=O(h⁴)，得：

方程组（1-48）的解有无穷多个，每组解都确定一个三阶龙格-库塔法的公式。比较简单且重要的一组解是R₁=1/6、R₂=4/6、R₃=1/6、a₂=1/2、a₃=1、b₂₁=1/2、b₃₁=-1、b₃₂=2，它对应的是库塔公式（Kutta's third-order method），如下：

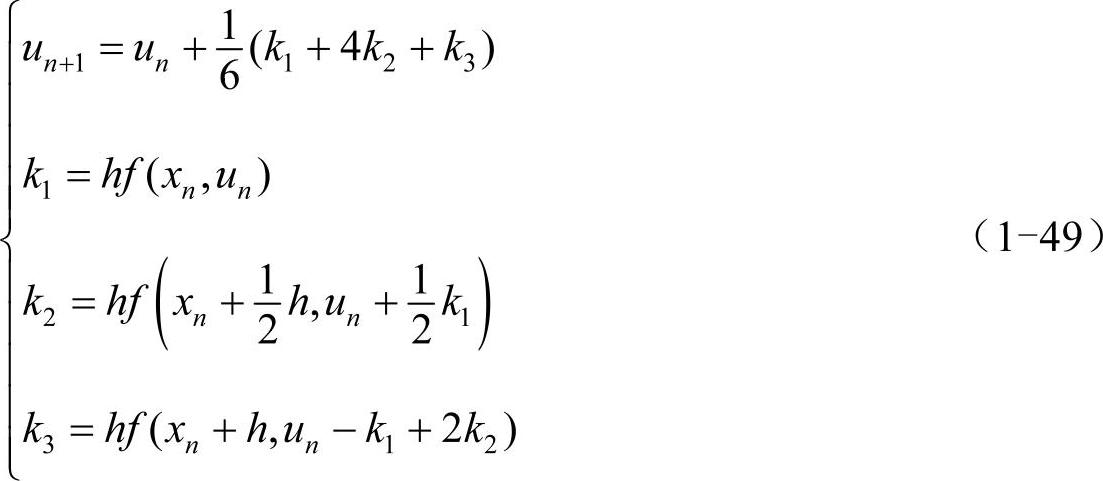
类似地，r=4时，龙格-库塔法的递推公式的形式为：

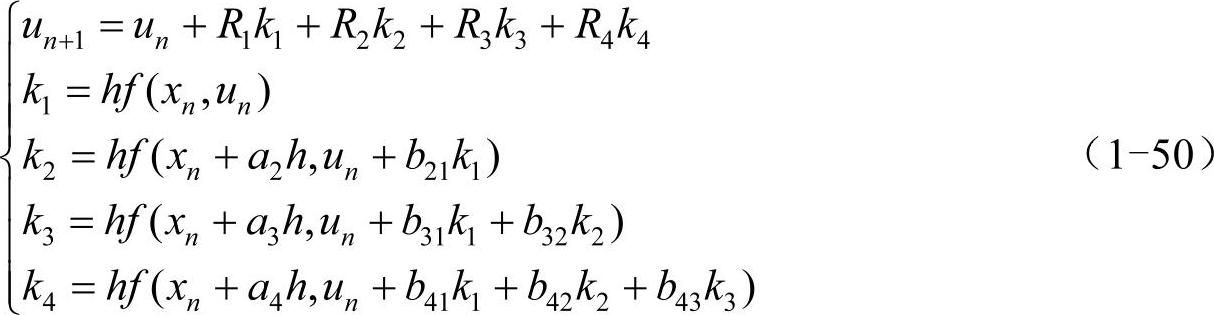
在局部截断误差为O(h⁵)的前提下，得到关于上式中待定常数的方程组的过程比较复杂，这里从略。下面给出两组常用的四阶龙格-库塔法的公式。

标准四阶龙格-库塔公式（classic fourth-order method）：

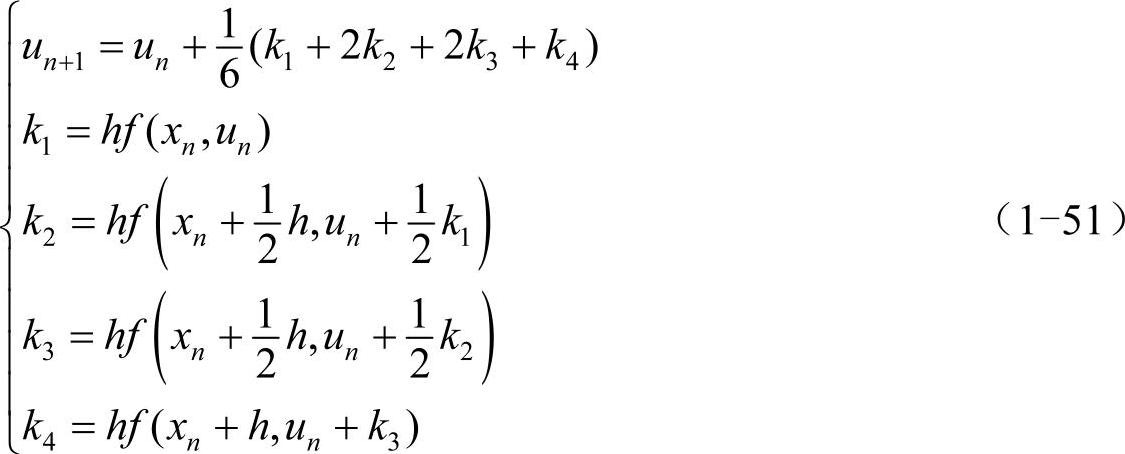
吉尔（Gill）公式：

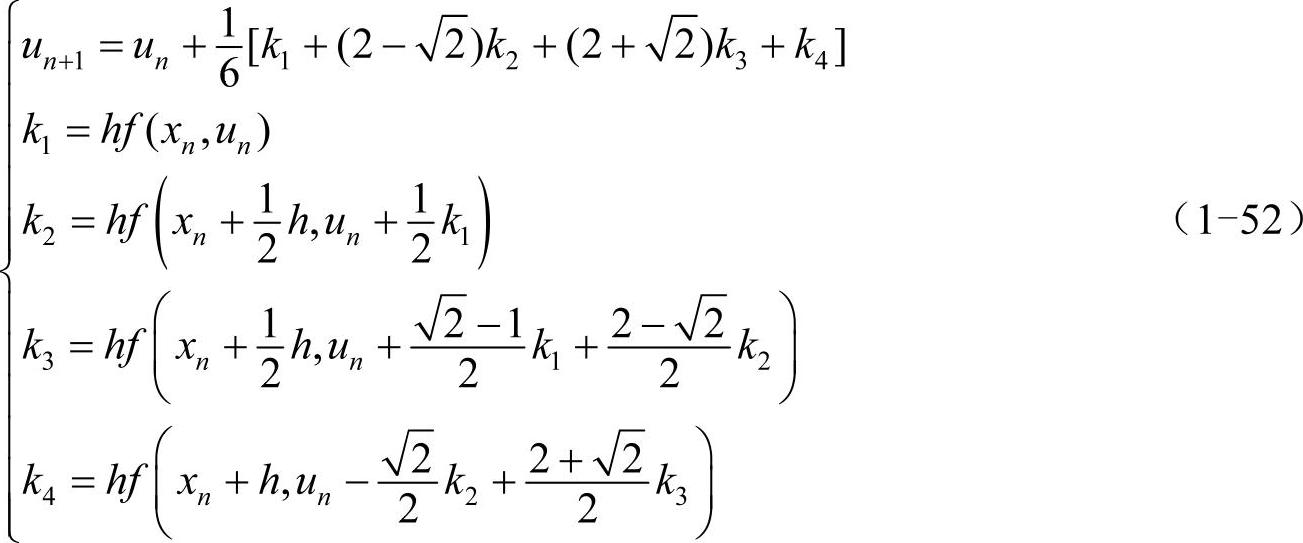
需要强调的是，r的取值并不总是和精度的阶数相同，二者关系如表1-1所示。随着r的增加，每递推一步的运算量也在增加，对于多数实际问题，四阶龙格-库塔法的精度就已经足够了，因此它也是最常用的龙格-库塔法。

表1-1 r与计算精度的关系