欧拉法(Eulermethod)的核心就是将导数(微商)近似为差商。将导数近似为向前差商,则有:

代入式(1-1)中的第1个式子,得:
u(xn+1)=u(xn)+hf(xn,u(xn)) (1-3)
用un和un+1近似代替u(xn)和u(xn+1),得:
un+1=un+hf(xn,un) (1-4)
上式称为欧拉法,其中n=0,1,…。若已知u0的取值,就可以用递推公式(1-4)步进式地计算出x1,x2,…处的u1,u2,…。欧拉法的几何意义如图1-1所示,从点(x0,u0)出发,以f(x0,u0)为斜率做一直线段,与直线x=x1交于点(x1,u1),该交点的纵坐标u1就是u(x)在该处的取值u(x1)的近似。再从点(x1,u1)出发,以f(x1,u1)为斜率做一直线段,与直线x=x2交于(x2,u2),其纵坐标u2就是u(x2)的近似。继续重复这一过程,最终获得一条折线作为曲线u(x)的近似,因此欧拉法也叫折线法。
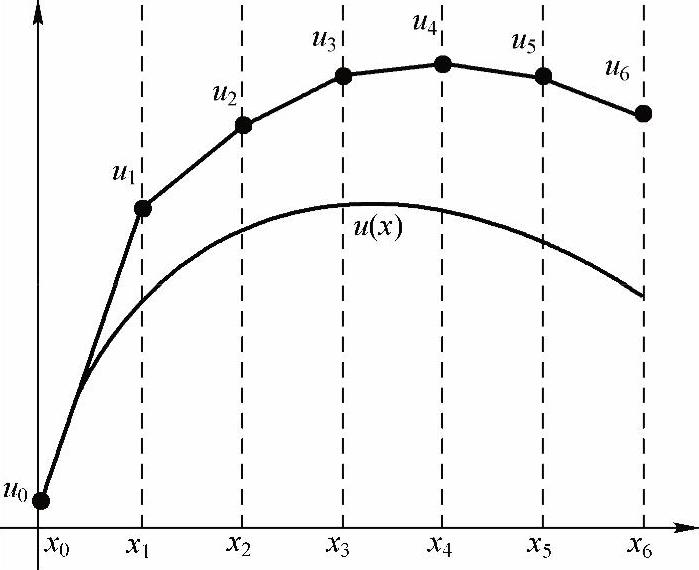
图1-1 欧拉法的几何意义
如果将导数近似为向后差商,有:(https://www.xing528.com)

同样代入式(1-1)中的第1个式子,并用un和un+1近似代替u(xn)和u(xn+1),得:

上式称为后退的欧拉法(backward Euler method),其中n=0,1,…。它与欧拉法截然不同,式(1-4)可直接用xn和un计算得到un+1,而式(1-6)等号两边同时包含un+1,无法直接计算un+1具体数值,所以也称为隐式欧拉法(implicit Euler method)。
如果将导数近似为中心差商:

代入式(1-1)中的第1个式子,并用un-1和un+1近似代替u(xn-1)和u(xn+1),得:
un+1=un-1+2hf(xn,un) (1-8)
用上式计算un+1的时候需要un-1和un的值,所以称其为二步欧拉法。实际使用二步欧拉法的时候,起初就要用到u0和u1的取值,若u1未知,一般就先用欧拉法求出u1的值,再使用二步欧拉法。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




