耦合双球线摆的力学模型及微分方程

古人类的双臂振浪飞摆运动的模式，为前半程都是近似的自由下摆过程，在中后半程收缩相关肌肉群加速摆动。采用耦合双球线摆模型分析，设定一次摆动的总时间由前半程的自由摆时间t1和后半程的驱动摆时间t2构成，t1决定于身体本身的结构，而t2则决定于肌肉收缩速度，所以一般t1要远大于t2。ω为系统频率，ω1为上摆频率，通过串联耦合摆模型的摆动频率极值分析来定性解释人体结构上下肢比例的进化。

依此模型的微积分方程分析小角度（＜5°）时简谐摆动频率：考虑人猿臂行方式为低频大幅摆动特征，由此解得两个摆球初始摆动角度之间的关系：

当模型上摆频率ω1确定时，计算得出下面单摆的频率最大也就是l2=0时，简谐摆动频率最大，且等于ω1。这就解释了长臂猿收腹将整个下肢提至腹前，可减小有效摆长，加速摆动，提高身体整体摆动频率。

图1-8 双球线摆简易模型及拉力最大化的质量分布^[12]

当模型l2=l1+l2为常数，那么l1/l2=1∶1时，其系统小角度摆动频率取得极大值。这也就解释了几百万年前树栖时期人类体型都必须尽量符合合适的比例，才能使其摆得最高、最远，或者最快。

当模型中两个摆长相等，初始摆角比值为，两个摆锤的总质量一定时，拉力最大化应该将所有质量分布于下面摆锤，下面摆锤下降的高度更大，其角速度和速度也都大于上面摆锤，可以使其摆至最低点时轴向加速度最大，也使得摆对支点的拉力最大。因此，古人类摆动时为伸直腿至重心下移最大，产生对树枝的拉力最大，于是反弹力最大，一次性可跳得最远。

从上面分析可以看出，为了将系统频率最大化，质量应该尽量分布于中间，而为了将拉力最大化，质量应该分布于底端。在自然进化中，速度是优越于力量的，频率最大化是速度最大化的一个重要方面，故而频率是优先于力量的。观察具有臂行振荡运动的长臂猿，发现它们平时多采用的是收腿摆动方式，这种方式显然是频率较快的，但是当跨越较远距离时，则展开身体（图1-9），加大旋转半径，从而加大摆动的弧度和力量，但即使是展开身体，其身体质量中心也是在中部稍偏下的位置，因为这样才可以使得大角度摆动时的频率最快。

图1-9 长臂猿悬挂摆荡运动^[13]

采用数学软件Mathematica 8.0，对模型的大角度摆动微分方程进行系统频率极值分析。串联线摆将发生合拍现象，双摆锤同时摆过中点，随着初始摆角的增加，初始摆角比值θ1（0）/θ2（0）也随之增加，θ2（0）的增加要快于θ1（0），且摆动周期也随初始摆动角度而增加，但是增加得比较慢，这是因为摆动周期主要由有效摆长决定，而与摆角的关系不大。当初始角度5°＜θ1（0）＜45°时，随着初始摆角的增加，计算显示：l1=l2=1，摆动周期最小，频率最大。这和理论值是一致的。θ1（0）＞45°，无论怎么调整θ2（0）都无法形成合拍摆动。

如何在最短时间里下降相同的高度，显然比摆长一定时如何在最短时间摆动相等的角度更具有物理意义。计算得出重心下降高度达到l1=l2=1处，摆动频率最高。

以上分析的是自由下摆过程，实际上，人体摆动时前半程以自由摆动为主，后半程则肌肉收缩加速摆动，但是两个过程对于身体结构要求是类似的，后半程的主动摆动也同样要求上下长度比值约为1。这种对称性结构具有多方面的运动优势。当然，古人类的身体长度比例均不严格符合上述1∶1的结构，而是近似为此比例。

根据耦合双球线摆的分析，确定了人体的长度比例为1∶1，即腰部上下比例为1∶1，这个比例可以实现耦合共振，从而达到能使其摆得最高、最远，或者最快。为了满足这个要求，人体的进化均围绕此目的进行系统性结构演化。

为了能更准确地模拟古人类树栖时期的运动，这里采用一个比串联线摆更接近实际人体结构形态的复摆模型。参照南方古猿体型，采用一个比串联线摆更接近实际人体结构形态的复摆模型，通过摆动频率极值分析推测出古人类怎样的身体比例才是最适合双臂摆动的。

对此模型做以下简化假设：

1.上臂与前臂（肘关节到第二指关节）的长度比为：1∶1.5。对比南方古猿身体结构，这与现代人的上肢长度比例是相似的。

2.大腿与小腿（加足长）长度比为：1∶1.5。

3.l0为树枝摆动半径。

4.上肢长度为l1，躯干长度为l2，其中胸部为l2a，腰腹为l2b，下肢长度为l3，臀部长度为l4=（1/8）l3。

5.为简化计算，设身体各部位密度一致：ρ=1。

6.从上至下截面积设为：S1（前臂），S2（大臂），S3（胸），S4（腰腹），S5（大腿），S6（臀部），S7（小腿）。

7.小腿与大腿夹角α约为45°（根据现代运动员做双臂摆图片，这个角度有利于踢腿，参照图1-10左图）。

图1-10 古人类臂行模型及双臂摆动动作^[14]

8.将头部和胸部作为一个整体考虑，古人的头部大小只有现代人头部的1/3，按比例的话是现代人的1/2。

对于树栖动物来说，体重是决定其运动方式的最主要因素。

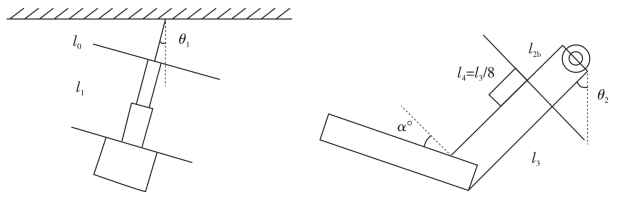
图1-11 上半身有效摆长及下半身有效摆长^[15](www.xing528.com)

参考现代人体以及古人类化石，分别对三组体围数据进行分析。以摆动频率最大为目的，通过调整上肢、躯干和下肢的长度，获得最佳的身材比例。

第一组：流线型，胸、腰、臀三个部位围度值相差较小，且整个体型较为修长。

第二组：匀称型，胸和臀围较大，腰腹部位较细，身体较匀称强壮。

第三组：短粗型，与匀称型相比，其腰腹围度较大，体型短粗。

然后再对三组结果进行比较分析。

表1-1 人体结构形态复摆模型分析体型参数^[16]

表1-2 摆动频率极值点上下肢比例计算结果^[17]

注：l1为上肢长，l3为下肢长，l1/l3为上下肢比例。

根据模型微积分计算发现，摆的中部的躯干围度的增加有利于频率的加快，且胸部的增加效果好于腰腹部，这是因为胸部位置更高的缘故，但是增加的效果是递减的，且体重的增加必然会加大上肢的负担。

从南方古猿较细长的腰椎来看，估计他们腰腹围度是不大的，虽然他们下胸骨和骨盆都比较宽阔，但这种构造是为了增加腹肌的作用力矩，提高摆腿速度，如果腹部前凸，就像大猩猩一样，则将严重减小摆腿的幅度，故我们认为南方古猿腰腹部位是比较平坦的，其围度要小于胸围和臀围，这一点与身材较为匀称的现代人类似。

图1-3B显示南方古猿露西下胸骨宽大，而且向前凸起，她的腰椎较长，有的研究者认为她具有六节腰椎。另外，露西臀部异常宽大，相较于黑猩猩，现代人髋骨短而宽阔，而露西的髋骨比现代人的髋骨要宽大得多。

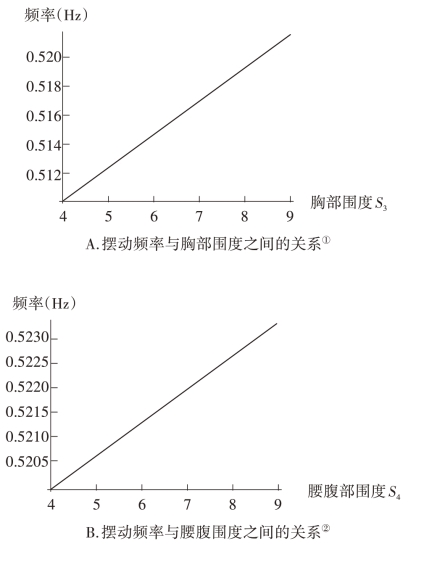
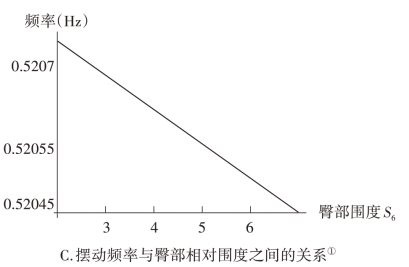
图1-12 摆动频率与各部位围度的关系

从自由摆动的角度来看，胸腹部位增加质量是有利于加快摆动速度的，但是腹部围度过度地增加显然会增加收腹前摆的难度和减小摆动的幅度。南方古猿露西的下胸部宽大外突，这是与其宽阔的骨盆相对应的。南方古猿骨架的下胸腔和盆腔都比较宽阔，而腰椎较长。即使是体型匀称的现代人也有上述特征，人体的腰腹部位的肌肉扁平，此部位的肌肉经过锻炼只会变得强壮有力而体积却变化不大，所以体脂较少的人腰腹都比较细。从人体美学的角度看，无论男女，都以腰细为美，因为腰腹相对较细意味着身体运动灵活。

因为臀部位于摆的中下位置，臀部质量的增加会加大有效摆长，从而降低摆动频率，但是下降的程度非常微弱，与胸腹相比，摆动频率与臀部大小几乎没有多大关系。南方古猿臀部宽大的主要原因是为了在振浪过程中下肢的摆动特别是侧摆时更快更有力，只有宽大强壮的臀部才能使振浪的效果更佳。

根据模型分析计算古人（以南方古猿露西为参考）大角度摆动的结果，显示最为接近南方古猿上下肢比例数值的是匀称体型，分别为0.98和0.91，稍大于化石分析的结果。

表1-3 摆动频率极值点上下肢比例计算结果^[18]

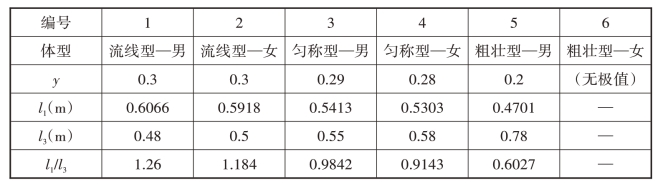
注：l1为上肢长，l3为下肢长，l1/l3为上下肢比例。

由于计算忽略了树枝本身的摇摆导致的有效摆长的增加，假设匀称体型的男女两性导致树枝摆动增加的有效摆长为5厘米和4厘米，则匀称体型男女上下肢比例分别为0.8868和0.8284。粗壮型女性由于其摆动频率随着下肢的长度增加迅速加快，从而完全掩盖了其下降的趋势，所以没有出现极值点。

南方古猿上下肢长度比例在84%～92%之间，比如化石标本露西上肢肱骨长237厘米，股骨长280.5厘米，比例为84.5%。从计算结果来看，古人类体型既不是非常修长的流线型，也不是又短又粗的圆桶型，而是较为匀称的体型，即要求腰腹部位围度比胸部和臀部围度更小。南方古猿虽然下胸骨和髋部都很宽阔，但是我们认为其腰围并不会很大。

在所有的人猿中，黑猩猩、猩猩、大猩猩的身体都是相对比较粗壮的，唯有人类和长臂猿的身体是修长的（图1-13）。这是因为只有修长的体型才更加容易在摆动过程中拉伸身体和储存势能，而粗壮的体型则刚度太大，难以在摆动中获得势能。^[19]

图1-13 人与黑猩猩体型及股骨形态比较^[20]