现代三维扫描技术的发展使得三维模型数据呈现高速的增长状态,与此同时,模型的大小同样增长迅速,上G大小的模型已经非常常见。随着图形学硬件性能的提高,现代计算机系统的图形渲染能力随之提高,但仍然无法满足当前艺术级的图形渲染能力。因此在渲染过程中的实时模型简化方法会被大量应用,这些模型简化方法的最典型代表就是LOD技术。
LOD技术将一个模型简化为多个不同的三角形分辨率层次,每个层次包含不同的细节程度,在实际绘制过程中,根据对视觉的贡献率选择不同的分辨率层次,当该模型在场景中的重要性降低时,选择较低分辨率的模型表示层次,当离观察者较近或非常重要时,使用更高分辨率的模型。图6-1所示为LOD方法保存的不同分辨率的模型。
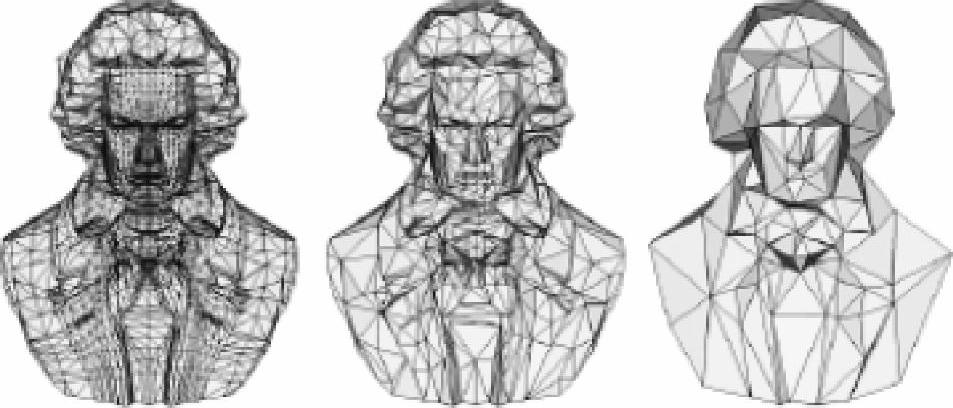
图6-1 LOD方法保存的不同分辨率的模型
目前LOD技术中,有离散LOD、连续LOD、视点相关的LOD和层次LOD几种[17]。离散LOD是传统的LOD方法,它将模型预处理为互相独立的细节层次模型,在运行时根据该模型对整个场景的贡献率选择不同的LOD层次,因此称为离散LOD。离散LOD的最显著的优势在于编程实现较为容易,而且该方法适用于所用图形加速硬件。离散LOD方法可以被编译成三角带、显示列表、顶点数组等,进一步加速显示性能。但离散LOD的缺陷是无法应用于一些形状特殊组织结构的模型简化,对于大模型的简化效果并不好。
连续LOD在1976年提出,相对于传统的离散LOD方法,连续LOD在运行时提取LOD细节,使得简化在运行时进行,根据当前所需的细节程度,准确地简化出一个特定的层次细节,而离散LOD是选择一个近似的预创建的模型。在相同绘制效果条件下,连续LOD使用更少的三角形,使得系统绘制性能进一步提高。连续LOD的另一个优点是可以实现层次间的平滑过渡,减少了pops的出现。
视点相关的LOD方法针对当前的视点位置和视线方向,选择最佳的层次表示。在显示过程中,同一个模型的不同部分可能使用不同的LOD细节层次,距离视点越近的部分使用越高的分辨率,而较远的部分使用较低的分辨率。侧影轮廓部分使用更高的分辨率,而正对视点的位置使用较低的分辨率。在同样三角形数目的条件下,视点相关的LOD方法比连续LOD具有更好的精细度,这是因为视点相关的LOD方法将多边形分配在最需要的位置上。视点相关的LOD对超大模型的简化效果要更好。
层次LOD是针对于大量小模型的显示问题而设计,在模型重要性较低时,将若干个小物体组合为一个整体进行简化而不是对每个物体进行简化,解决了小模型的显示问题。层次LOD与视点相关LOD具有同样的稳定性,将整个场景看作一个整体进行简化。
在LOD方法的使用中,Heok[17]和何晖光[88]分别给出了一个LOD方法的综述和网格模型简化的综述,潘志庚[89]给出了多细节层次模型自动生成技术的综述,Chadwick[90]给出了一种动画角色的层次化创建方法,Hoppe[91,92]提出了一种不规则网格的离散简化与渐进式简化方法,Cignoni[93]比较了各种网格简化算法的优劣,Ogren[94]提出了一种基于连续LOD的实时地形渲染算法,2005年张昌明等[95]提出了一种基于边折叠的多边形网格模型简化算法,在减少屏幕误差的前提下提高图形绘制速度。(https://www.xing528.com)
LOD简化过程可以分为多边形简化和非多边形简化,对于非多边形简化包括样条曲面简化、体模型简化以及基于图像的模型的简化。大多数LOD简化算法是针对多边形简化的。多边形LOD简化算法可以分为两部分,一部分是几何简化,另一部分是拓扑简化。几何简化主要是减少几何元素(顶点、边、三角形等)的数目,拓扑简化主要为了减少孔洞的数目。一些复杂的简化算法常常既包含几何简化又包含拓扑简化。
几何简化大体可以分为如下几类:
(1)顶点剔除。该方法主要是减少模型中的“Pluck”顶点,每剔除一个顶点,其周围的相邻三角形就同时被删除,同时通过重新三角化补齐由于删除顶点造成的孔洞。顶点剔除方法可以应用于所有的多边形模型。
(2)顶点合并。顶点合并法将相邻的顶点进行合并,重新计算一个合适的顶点替代这些顶点及其被合并的三角形,简化之后密集区域的顶点和三角形被合并成一个顶点。
(3)边删除。在边删除算法中,一条边两端的顶点合并为一个顶点,同时删除该边及其两侧的三角形。该方法的优点是替代顶点的位置可以自由选择,而且不需要执行较为复杂的区域三角化算法。通用的边删除算法包含两个步骤:一个是选择需要合并的边,通常是根据视觉差来决定的,二是计算替代顶点的位置。
(4)顶点对收缩。顶点对收缩是一个比边删除更加稳定的算法,该算法支持任意的一对顶点进行合并,不论它们是否有共享边。
(5)面合并。面合并算法支持共面面片的合并,从而形成“超面”。在合并过程中,整个网格通过聚簇算法分为几个区域,区域内的内部顶点全部删除,剩下的顶点形成一个简化的网格模型,最后将模型中非平面的“超面”进行三角化即可。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




