基于统一基础模型的细节保持变形-计算机图形学与角色群组仿真

细节保持是减小变形失真提高变形逼真度的重要方法，它通过分离原几何模型为基础模型和细节模型，在变形中只处理基础模型，变形后将细节模型再合并到基础模型上，细节模型不参与计算从而减少细节丢失。

广义的模型细节，是指模型表面或内部各顶点之间的变化率，如LOD算法中将模型细节分为粗细不同的层次模型^[17]。狭义的模型细节，是特指梯度等参数变化率较大的部分，即高频部分。基础模型一般分辨率较低，顶点间的变化率小，细节模型包含高变化率的模型细节，是原模型网格与基础模型的差。大部分的模型处理或变形过程常常会使模型丢失尖角凸起等细节，模型表面变得平缓。细节保持的变形方法将原始模型分离为一个分辨率较低的基础模型和若干个高变化率的细节模型，在变形过程中，只对基础模型进行变形，变形后再将细节模型合成到变形后的基础模型上，从而保持模型上的高频细节。

细节保持方法中的细节模型，需要通过原模型与基础模型进行径向求差运算获得，每个顶点表征的是原模型与基础模型的差。为更好地保持模型细节，使用的细节模型与原始模型拓扑相同，两模型顶点一一对应。统一基础模型是规则网格，而原始模型一般是不规则网格，在径向求差的过程中，使用三线性采样，获取基础模型的径向值。变形基础模型之后，再将该细节模型合成到基础模型上，实现细节保持的模型变形。

图4-8所示为细节模型计算的纵切面图，其中R₀是变形焦点，P₀Q₀′为变形控制曲线，平面R₀P₀Q₀′为变形平面，P₁P₂Q₁′Q₂′是原模型对应的基础模型，不规则曲线M和N是原物体模型的交线。

控制线交点C可以通过向量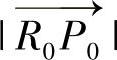旋转获得，旋转后的向量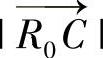的旋转角等于变形方向角，俯仰角α_A为顶点A变形旋转角，可以根据式（4-8）求得。

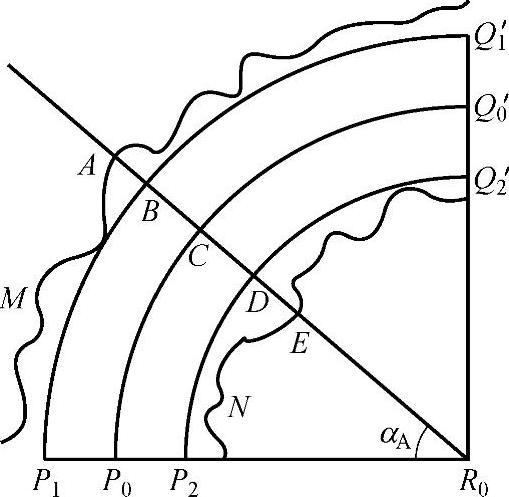
图4-8细节模型计算的纵切面图

(www.xing528.com)

以模型顶点A为例，其模型细节的获取方法是，作一过顶点A的横切面，R₀A为该切面在变形平面中的投影，该切面与原模型以及基础模型相交获得的横切面如图4-9所示，其中C为控制曲线与切面的交点，圆BQD为基础模型与切面的交线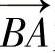，为顶点A对应的模型细节值，即向量与的差。

针对原模型中的每一个顶点，通过该点与对应控制点的距离求得模型细节值，即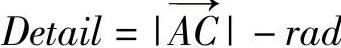，其中rad为基础模型的圆柱体底面半径。保存各顶点的旋转角α_i、横切面内方向角θ_i以及细节值，得到变形所需的细节模型。

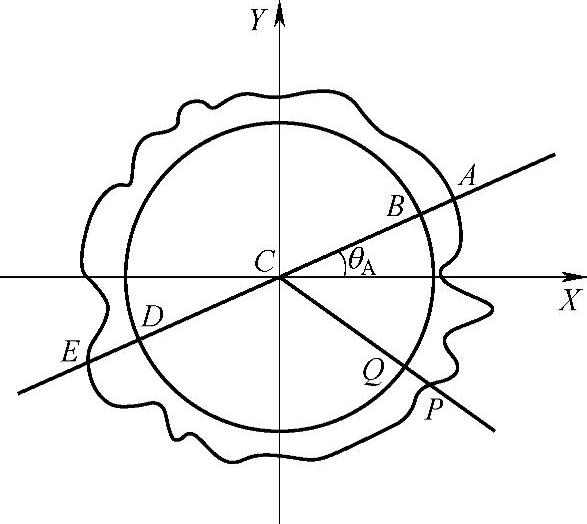
图4-9细节模型计算的横切面示意图

在变形过程中，对基础模型进行变形计算，然后将细节模型合成到基础模型上，以还原原模型的细节。细节模型的合成实际上是其获取过程的反向运算，对于细节模型的任一顶点A，根据其α和θ值求得其在基础模型上的投影点B。

细节模型与基础模型的合成方法是，采用三线性插值法获得基础模型投影点B的坐标，从而得到向量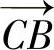，将顶点A的模型细节值与向量叠加求得向量，根据和C点位置求得顶点A的变形后位置。针对细节模型的每一顶点，均采样其对应的基础网格模型坐标，然后叠加模型细节值，即可获得整个模型的最终变形结果。