表面积保持的统一基础模型变形

细节是物体模型的一种表征相邻顶点之间变化梯度的属性，细节保持可以看做是模型的一种属性保持手段，对提高变形结果真实感具有重要的作用。表面积是柔软物体和壳体的另一大特征属性，但目前的变形方法对它关注不足。柔软物体如软体动物、橡胶以及毛绒玩具等，它们的一个显著特征是表面水平可拉伸性低但垂直可挤压性高，总面积总试图保持不变，弯曲方向最外侧在变形过程中不会被拉伸，而在弯曲方向内侧受挤压部分会出现多条凹凸纹皱褶。

目前的变形方法大多针对刚体变形，而针对柔软物体或可弯曲物体的变形研究较少。实现柔软物体的变形一般使用基于物理的方法，但这种方法需要大量的计算，大多无法达到实时变形。

本章提出的统一基础模型，由于规则网格的易处理性，可以在实时处理的前提下，仿真柔软物体的表面变形皱褶，同时实现变形过程中的表面积保持。与基于物理的变形方法相比，基于统一基础模型的柔软物体变形有如下优点：

（1）变形算法简单、计算速度快，可以实时地产生能接受的变形结果；

（2）物体的柔软度是可控的，可以通过调整变形参数，改变皱褶的间隔和皱褶数量，变形模型会自动调节皱褶的形状，保持表面积不变。

以下是基于统一基础模型的表面积保持原理及其实现方法。

统一基础模型的规则网格顶点可以划分为若干列，每一列顶点在本书中称之为顶点列。弯曲变形除弯曲最外侧顶点列外，其余各顶点列的表面均被挤压。各列在弯曲与拉直状态的列长度比为压缩系数，该系数越小表示压缩程度越大，压缩系数最大为1表示未被压缩。该系数表征基础模型的变化率，在变形过程中，将据此计算阻尼振荡曲线函数，实现基础模型的表面积保持。

在统一基础模型变形中，是使用阻尼振荡曲线叠加到模型表面来实现表面积保持的，叠加过程需首先计算基础模型在弯曲变形过程中的表面积受压缩系数，根据该系数计算阻尼振荡曲线函数，使曲线的总长度等于拉直状态下的顶点列长度，从而实现模型变形中的表面积保持，并用曲线的形状模拟柔软物体弯曲变形内侧的皱褶。

在基础模型网格垂直截面图4-3中，最外侧顶点列P₁Q₁弯曲变为P₁Q′₁，该列在变形中未被压缩即|P₁Q₁|=|P₁Q₁′|，而对于其他列上的任一顶点A，其所在列的受压缩系数可推导为式（4-4），即顶点列的圆弧半径与最外侧圆弧半径之比。

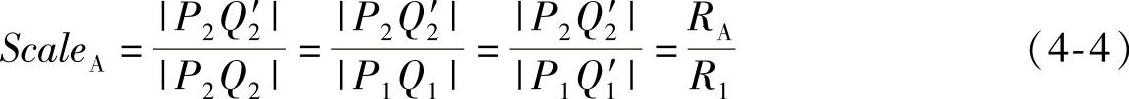
为继续求解式（4-4）获得两圆弧半径之比，由基础模型变形的横切面图4-4中可以得出，B为A在变形平面上的垂点，在变形平面中弯曲变形时点A与B的弯曲圆弧半径相同，因此顶点A的所在圆弧半径可通过点B的圆弧半径求得，顶点A的基础模型弯曲压缩系数可由式（4-5）求得，其中rad为基础模型网格的底面半径。

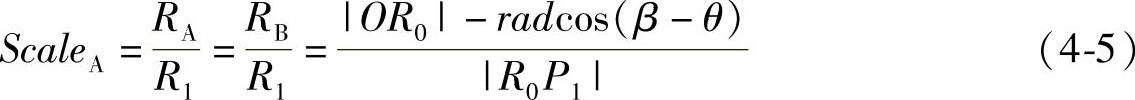
在基础模型网格变形过程中，最外侧顶点列P₁Q₁长度不变，其他所有顶点列的长度都会被压缩，造成表面积减少。为实现变形表面积保持，引入新的皱褶仿真函数。经研究发现，表面皱褶在变形区域中中间部分起伏最大，向两端逐渐减弱，该特征与振幅递减的阻尼振荡曲线相同，可以采用该曲线仿真物体表面的皱褶，并根据模型表面各处压缩系数计算曲线参数，获得表面积保持的基础模型网格。阻尼振荡曲线的函数定义见式（4-6）。

(www.xing528.com)

式中，A是振荡曲线的最大振幅；x_max是振荡曲线的最大振荡时间；k是振荡周期数，k越大则振荡次数多，在变形仿真中是用户设定的形状因子，决定皱褶个数。

通过保持各顶点列在变形前后的总长度不变，实现基础模型变形前后的表面积保持不变，也就是说，通过振荡曲线调整模型顶点位置，使顶点列弯曲状态下的总长度等于拉直状态的总长度。基础模型的每一顶点列共用一条阻尼振荡曲线，曲线从中间向两端对称延伸，其长度可用式（4-7）计算。

式中，f′（x）是阻尼振荡曲线函数的微分；X_max是最大振荡时间，即该顶点列的圆弧半长度X_max=height·Scale/2。

最大振幅A是调节振荡曲线总长度的主要参数，根据顶点列在变形前后的总长度不变的条件即length=height，可求得参数A。由于振荡曲线函数的微分形式复杂，积分困难，本节采用将整个压缩系数空间按0.01间隔划分，采用数值方法求得每个压缩系数所对应的阻尼曲线最大振幅A。

在基础模型表面积保持计算中，根据各顶点在弯曲圆弧上的位置，通过阻尼振荡曲线函数计算该顶点的函数值，该值即为该顶点为仿真皱褶所需要的高度调整值。依次计算各列顶点，求得变形基础模型上所有顶点的高度调整值，然后根据该值调节基础模型网格顶点的位置，调节方法是，对于每个顶点，从其变形横截面上的控制曲线交点，向该顶点发射一条射线，沿该射线方向叠加高度调节值，计算顶点的新位置。调节之后，变形基础模型的各顶点列在变形过程中可保持长度不变，从而实现整个基础模型在变形中保持表面积不变。

非表面积保持与表面积保持的基础模型网格在90°弯曲状态下的比较如图4-6所示。从变形网格状态中可以看出，表面积保持的变形更有一种受挤压感。从观察者的角度，表面积保持的变形更能体现出这是一个从其他状态变化得到的结果，而不是它的初始状态就是如此。

图4-7所示为基础模型在其他弯曲角度下的网格状态，从图中可以看出，受挤压的程度越大，表面皱褶越明显，皱褶也越尖锐，这也是柔软物体的表面积保持特性在受挤压时的实际效果。

图4-6 表面积保持的基础模型网格1

图4-7 表面积保持的基础模型网格2