基于规则网格构建的统一基础模型

一个完整的物体模型变形，可以通过对每一段独立的变形区域进行变形，然后再对变形后的网格根据控制点的位置变换坐标连为一个整体，最终实现整个模型的变形。物体的最基本变形方式是弯曲变形，各种形状的变形都可以由不同朝向和不同程度的基本弯曲组成。变形中心线的曲率最大处是该变形形状的控制点，根据控制点可以将整个变形物体分割为若干变形区域，每个变形区域中含有一个变形控制节点，每个控制节点与两侧的控制节点一起可以决定一段圆弧，每一段圆弧定义一个基本弯曲变形。

每一个基本的弯曲变形有两个表征：一是弯曲朝向和弯曲程度，分别用两个参数来定义这两个表征特性，弯曲方向角表示弯曲朝向，它的值为当前弯曲所在的平面与XOZ平面的夹角，在同一个弯曲平面中向左弯和向右弯的弯曲方向角差异180°；二是弯曲旋转角表示弯曲程度，它的值为圆柱体基础网格顶平面与底平面的夹角，该角度越大则弯曲程度越大。

本节针对一段独立的变形区域，根据其弯曲角度等形状参数，直接使用圆柱体网格作为基础模型，从而减少基础模型的获取计算步骤。图4-1所示为使用统一基础网格的基础模型构建示意图，统一基础模型的规则网格的半径取原模型的半径平均值，原模型凸出的部分将置于网格外，而凹进的部分将被网格包围。图4-2所示为原模型与统一基础模型网格的分视图，可以更清晰地看出原模型与统一基础模型网格的关系。

图4-1 使用统一基础网格的基础模型构建示意图

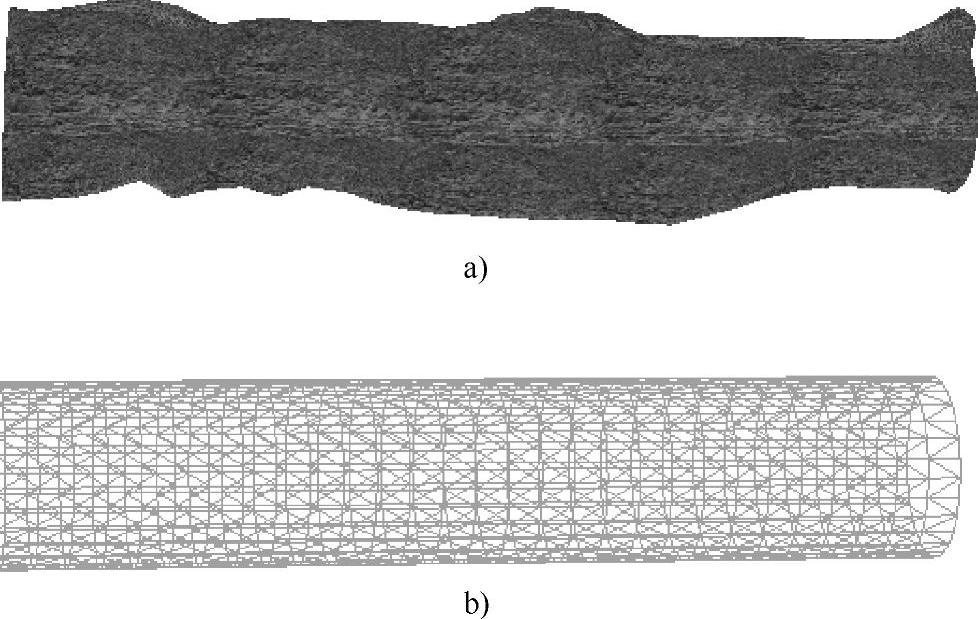
图4-2 原模型与统一基础模型网格的分视图

a）原模型 b）统一基础模型的网格(www.xing528.com)

统一基础模型的构建方法为：对于每个独立变形区域，变形基础模型的规则圆柱体网格底面为当前变形区域与上一区域的接合面，底面半径为当前区域的横切面半径均值，高为区域长度。基础模型网格顶点在模型中水平方向按照旋转角度θ、垂直方向按照Z坐标均匀分布。在三维模型的变形过程中，基础模型将通过弯曲旋转角度的改变或弯曲方向角度的改变实现变形。

直接使用规则网格模型作为基础模型的优点有如下几点：

（1）避免基础模型生成计算。基础模型一般通过模型简化或者低通滤波实现，需要大量的运算，在计算机图形学中，模型简化本身就是一个复杂问题，在细节保持的变形算法中，一般在预计算中进行基础网格的计算。根据原始模型的形状参数直接生成基础模型，避免了相当繁琐的基础模型生成步骤。

（2）提高基础模型的变形速度。一般的三维物体模型属于不规则网格，简化之后基础模型网格也是不规则网格。在不规则网格处理中，网格顶点之间的拓扑关系相当重要。不规则网格的变形，在处理模型顶点的时候，还需要考虑拓扑关系改变的处理，而规则网格的拓扑处理十分简单。

（3）规则网格有利于变形方法的硬件加速。不规则网格的顶点拓扑不确定性，造成其存储结构复杂，给模型处理带来很大的困难，同时也一直是一个困扰硬件加速的因素。通过使用规则网格的基础模型进行变形计算，有利于基础模型数据的快速存储与读取，也易于使用图形硬件加速变形的计算速度。

（4）规则网格的统一基础模型利于扩展变形算法的适用性。以往的各类变形方法，需要针对特定的几何模型计算变形基础模型，并设计不同的变形算法，通过直接使用形式统一的规则网格基础模型，使许多三维物体模型的基础模型变得十分相近，甚至相同，基础模型间的区别仅在于某些参数的不同，该算法在一定程度上提高了变形算法的通用性和可扩展性。