自适应网格面积保持技术

面积保持和体积保持是目前变形方法中减小模型形状整体失真的有效手段，在二维角色图像变形过程中一般使用面积保持。图像变形的面积保持特性可以有效地避免一些折叠、收缩类的不合理变形结果，以降低角色形状的失真度。

面积保持又分为全局面积保持和局部面积保持，全局面积保持是变形过程中整幅图像或整个角色的总面积保持不变，局部面积保持在变形过程中保证整幅图像总面积保持不变的同时，还要保持各个子区域面积不变。

在目前的图像变形方法中，面积保持已经成为一种必须实现的算法特性。自适应网格作为一种应用于二维角色图像变形的支持网格，同样也需要实现面积保持的特性。在以往的覆盖网格图像变形方法中，面积保持是通过放缩三角面片的大小来实现的。例如在Igarashi^[15]方法中通过分别计算每个对应三角形的面积变化系数，进行放缩变换，从而得到面积保持的变形结果。值得注意的是，这种放缩需要很多步的计算，放缩之后还需要对三角形进行拼接，这是一个很繁琐的计算过程。

相比于这种繁琐的面积保持计算方法，本章提出的自适应网格的面积保持，由以往的图像变形后调节，改进为变形前预测调节，从而可以更方便地实现变形过程中的面积保持。由于自适应网格是针对单个关节点进行构建的，各个关节点的变形计算是互相独立的，在变形过程中，只需要保持每个自适应网格的面积，即可实现局部面积保持特性。以下是自适应网格在变形过程中实现面积保持的原理及其计算方法。

自适应网格由三角带网格和长度补足矩形组成。在角色动作变形时长度补足矩形形状不变，其面积在变形中也保持不变。三角带网格负责实现角色的形状改变，当角色姿态变化时，关节点旋转角改变，自适应网格的形状将随之改变，各个三角形面积也会发生变化。

由自适应网格的构建过程可知，在变形过程中，长度调节矩形的面积不会改变，要保持网格总面积不变，只需保持变形前后三角带网格的总面积不变即可。在自适应网格变形中，通过调节两侧边缘曲线之间的X距离，可以保持三角带网格的总面积不变，从而实现自适应网格的总面积保持，亦即实现角色变形的局部面积保持。图3-4所示为面积保持原理图，其实现过程如下：

1.证明中心三角带总面积与矩形abcd面积相同

图3-4a中的三条曲线分别是自适应网格的中心双曲线和两侧边界双曲线。两侧双曲线由中心双曲线在X轴方向上平移得到，它们的形状参数相同，因此区域amb与dnc的面积相同。根据双曲线的性质，当渐近线表示的骨骼长度几倍于宽度时，端点处曲线与渐近线距离很近，所以aef、dgf、bpk和chk四个区域面积近似相同。综上可知，自适应网格的三角带部分面积与矩形abcd的面积相同。等效面积替换的过程如图3-4a所示。

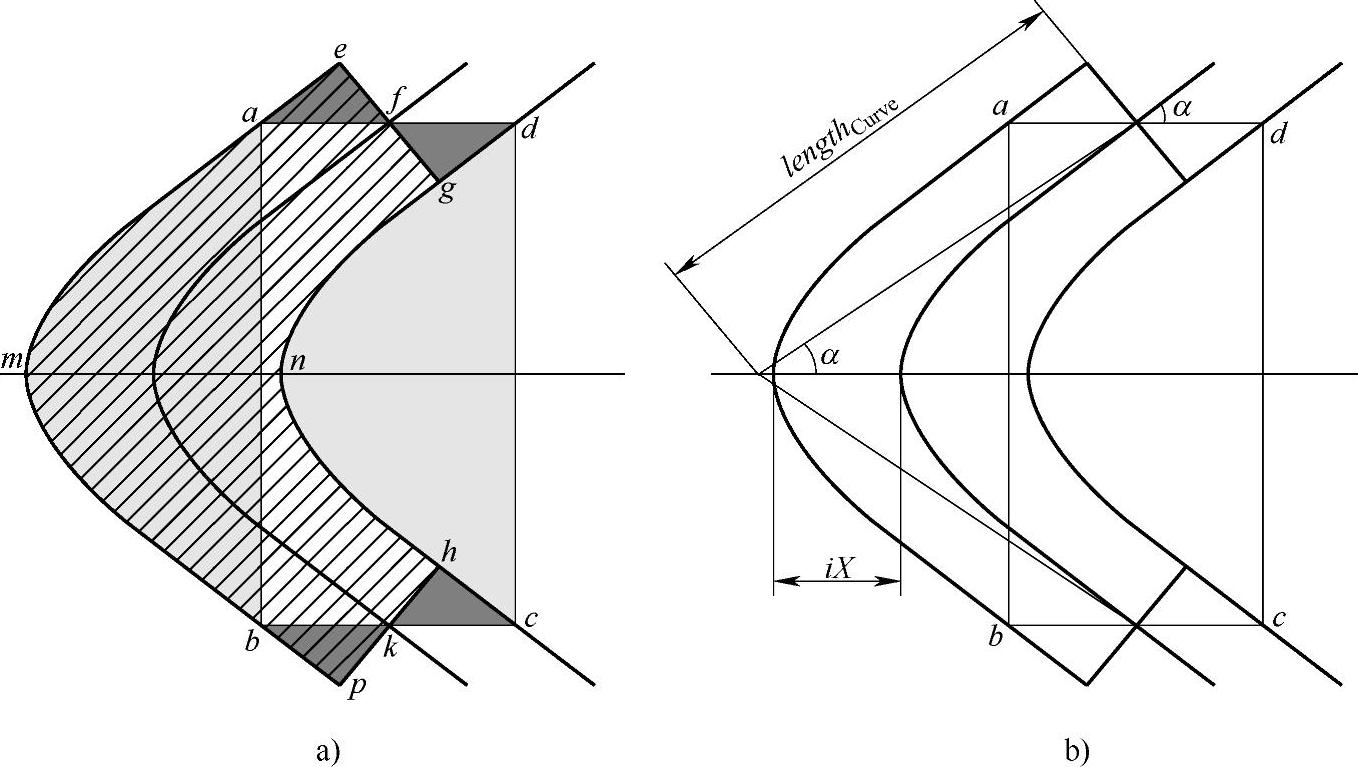
图3-4 自适应网格的面积保持原理图

a）等效面积替换示意图 b）面积计算示意图(www.xing528.com)

2.计算矩形abcd面积

根据双曲线渐近线的性质，图3-4b中矩形abcd的宽width=2iX，高height=2length_Curvesinα，而矩形abcd的面积S_abcd计算方法见式（3-8）。

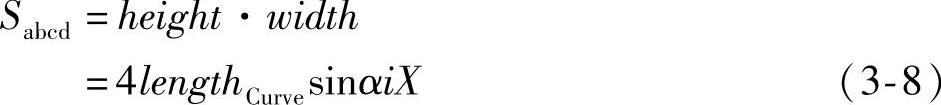
式中，length_Curve为曲线式骨骼模型中心三角带覆盖的骨骼长度；α为关节点两侧骨骼半夹角即渐近线倾斜角；iX为两侧曲线相对于中心线的X平移量。面积计算示意图如图3-4b所示。

3.计算两侧曲线的X平移量iX

角色的骨骼长度在变形中保持不变，由式（3-8）可知，要使变形模型中心三角带总面积保持不变，只需使sinαiX在变形中保持不变即可。iX计算公式可以表示为式（3-9），其中Bonewidth₀为初始状态的骨骼宽度。

iX=Bonewidth₀/sinα/2 （3-9）

通过等价三角形置换，以及计算两侧边界双曲线的平移距离iX，自适应网格的三角带面积即矩形abcd的面积可以用式（3-10）计算获得，此面积不随变形中骨骼的夹角变化而变化，因此在变形中可以保持面积不变。