在最近几年里,研究者们针对角色图像的变形提出了使用几何网格覆盖变形角色图像,通过变形网格形状实现图像变形的方法,使用图形的方法解决图像的问题,如2005年Igarashi[15]使用三角形辅助网格覆盖2D角色模型,使用最小二乘法求解网格自由顶点的位置获得变形结果。2006年Schaefer[73]间隔提取像素点作为辅助网格,使用最小二乘法求解网格自由顶点实现角色图像变形。2006年Weng[74]和Yoshioka[75]都将影响因素表达为方程组,分别使用非线性最小二乘法和约束最小二乘法求解该方程组,获得自由顶点坐标和图像变形结果。如图2-4所示为Igarashi[15]、Schaefer[73]和Weng[74]三种方法分别使用图像变形的覆盖网格示例。
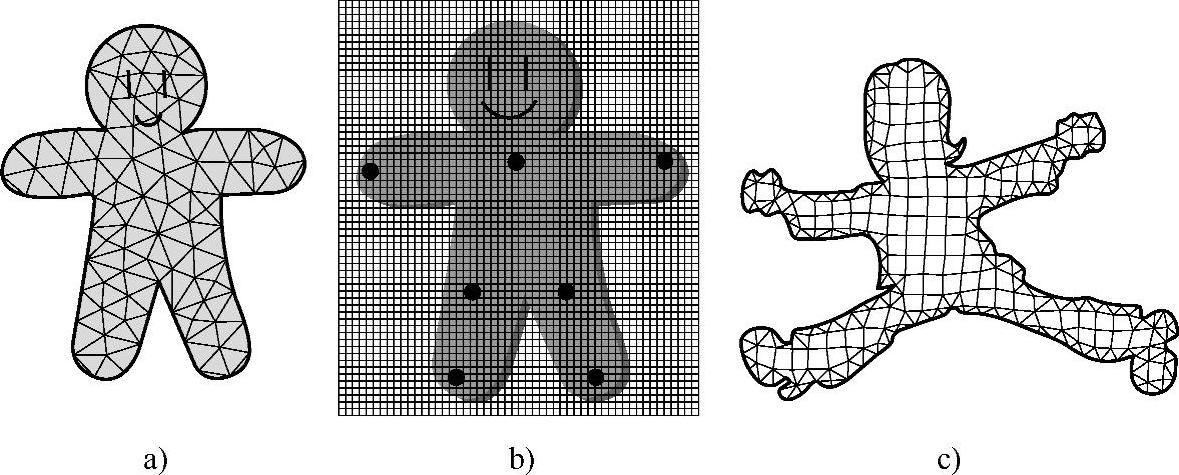
图2-4 图像变形的覆盖网格示例
a)Igarashi[15]的网格 b)Schaefer[73]的网格 c)Weng[74]的网格(https://www.xing528.com)
细节保持的三维模型变形技术越来越受到重视。细节保持可以减少高频细节信息丢失,从而解决变形处理中的尖角凸起细节丢失和模型表面平缓化的问题,提高变形逼真度。在细节保持的变形方法中,原始模型被分离为一个变化率较低的基础模型和若干个高变化率的细节模型,在变形中只对基础模型进行处理,变形后再将细节模型合成到基础模型上,由于细节模型不参与计算而减少了细节丢失。
细节保持的变形中常使用Laplacian坐标[76]和Poisson坐标[77]来实现。2003年Alexa[78]和Lipman[79]基于差分坐标实现了模型过渡和变形,在2006年Alexa[80]又探讨了离散Laplace和Poisson坐标的网格变形方法。2004年,Sorkine[76]和Yu[77]分别将Laplacian坐标和Poisson坐标用于表面网格模型编辑,为细节保持的模型变形提出了一种新的思路。2007年Nealen[16]和Wu[81]分别给出了基于素描的和基于骨骼的细节保持变形方法。
除细节保持外,体积保持也是一种重要的模型属性保持的方法,对提高变形结果真实感具有重要作用。Kobbelt[82]采用法向位移,对原始模型顶点在基础网格上的对应点进行位置编码,避免了对原始模型重采样造成的误差过大问题,但该变形方法会导致物体的体积变化。2003年Botsch[83]引入位移容积(Displace-ment Volume)概念,对局部棱柱体积进行位置编码,实现物体变形过程中的体积保持,但该方法计算量大、无法用于实时交互。2005年Choi[84]使用旋转角分解实现细节保持的大角度模型变形。2006年Huang[85]将模型映射到基础网格上进行变形,采用基于表面代替以往的基于空间的变形,实现简化模型的插值。2007年Oscar[86]使用控制变量集合表达变形,将变形模型简化为isoline,由isoline组成类似骨骼的虚拟控制结构,通过插值isoline和原模型实现低分辨率的模型变形。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




