确定电位滴定终点的方法-《仪器分析》

进行电位滴定时，边滴定边记录加入滴定剂的体积和电位计的电位读数。在滴定重点附近，因电位变化率增大，应减小滴定剂的加入量。最好每加入一滴记录一次数据。并保持每次加入滴定剂的体积相等，这样可使数据处理较为方便、准确。表12-2为一典型的电位滴定数据的记录和处理表。

表12-2　电位滴定典型数据表*

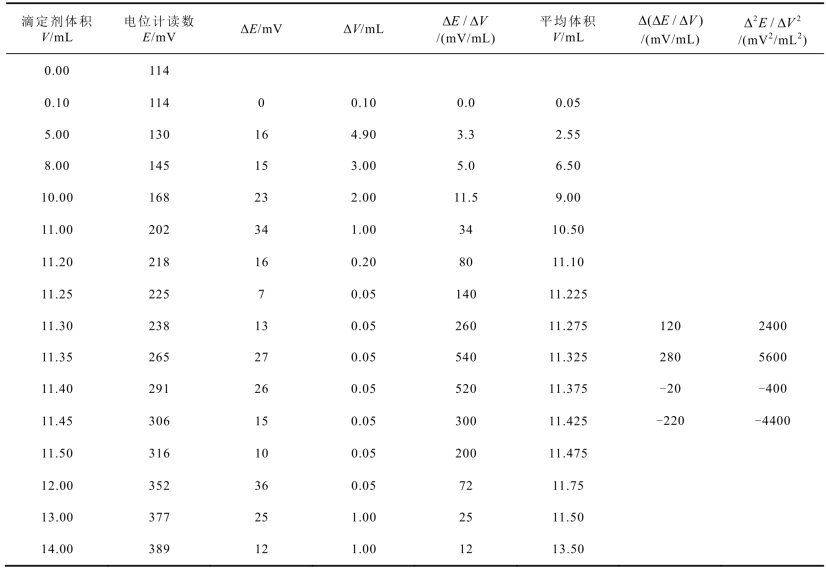
注*：ΔE值为同行中E值与其同列上方E值之差；ΔV值为同行中V值与其同列上方V值之差；Δ(ΔE/ΔV)值为同行　中ΔE/ΔV值与其同列上方ΔE/ΔV值之差。

下面介绍三种数据处理和滴定终点的方法。

（1）E-V曲线法

以表12-2中滴定剂体积V为横坐标，以电位计读数E（电位或电动势）为纵坐标作图，得到一条S形曲线，如图12-14（a）所示。曲线的转折点（拐点）即滴定终点。要求滴定化学计量点处的电位突跃明显。

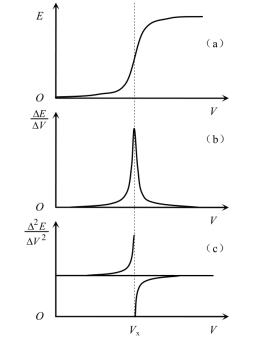
图12-14　滴定数据处理曲线(www.xing528.com)

（2）曲线法

用表12-2中ΔE/ΔV对平均体积（计算ΔE值时，前、后两体积的平均值）作图，得一峰状曲线，如图12-14（b）所示。峰状曲线的最高点即滴定终点。根据函数微分性质可知，该点的横坐标恰好与E-V曲线的拐点坐标重合，如图中垂直虚线所示。从表12-2中的数据可以看到，在化学计量点附近，ΔE/ΔV比E的变化率大得多，用曲线法确定终点也比较准确。选用的ΔV足够小，则有ΔE/ΔV →dE/dV，故曲线也称一阶导数曲线，该法称为一阶导数法。

（3）Δ2E/ΔV2-V曲线法

用表12-2中的Δ2E/ΔV2对V作图，得到一条具有两个极值的曲线，如图12-14（c）所示。该曲线可看成是E-V曲线的近似二阶导数曲线，所以该法又称为二阶导数法。按函数微分的性质，E-V曲线拐点的二阶导数为0，所以Δ2E/ΔV2-V曲线与纵坐标零线的的交点即滴定终点。由于滴定终点附近的曲线段可近似看成直线，因此二阶导数法的终点也可利用表12-2中的数据，不用作图法而用数学内插法予以确定。例如，从表中查得加入11.30mL滴定剂时，Δ2E/ΔV2=5600；加入11.35mL滴定剂时，Δ2E/ΔV2=-400。设滴定终点（即Δ2E/ΔV2=0）时加入滴定剂的体积为VxmL，则有

解得

Vx=11.35（mL）

利用上述作图法确定滴定终点，主要根据是化学计量点附近的测量数据。除非研究滴定的全过程，只需准确测量和记录化学计量点附近1～2mL的测量数据便可求得滴定终点。