【实验概述与思政要素】
杨氏模量是工程材料弹性形变的一个重要物理参数,它标志着材料抵抗弹性形变的能力。测量杨氏模量的方法很多,包括静态法(拉伸法)、动态法(共振法)、波速测量法以及其他一些测量方法。其中,静态拉伸法目前也是比较常用的一种测试方法,其优点是具有直观性和操作性;但由于其拉伸试验载荷大,加载速度慢,存在弛豫过程,不能真实反映材料的结构变化,对一些脆性材料无法测量,同时也不能测量在不同温度下的杨氏模量的大小。
杨氏模量,又称为弹性模量,一般用英文字母E来表示。在材料的弹性限度之内,它可以量化应力与应变之间的关系。虽然杨氏模量是以19世纪英国物理学家Thomas Young来命名,但是这一概念早在1727年就已经由瑞士数学家Leonhard Euler提出了。有关杨氏模量的实验,最早是在1782年由意大利科学家Giordano Riccati完成的,这一工作比Thomas Young早了25年。杨氏模量中的“模量”一词,英文单词是modulus,这一术语源于拉丁文modus,也就是测量的意思。
目前按照国家标准规定的方法是“动态悬挂法”(或称“动力学法”),它是目前工程技术上经常采用的一种测量杨氏模量方法。
所谓“动态法”就是将一根截面均匀的试样(如铜棒、钢棒)悬挂在两只传感器(一只激振,一只拾振)下,在其两端自由悬挂的条件下,使其自由振动,实验时测出试样振动时的固有基频,并根据试样的几何尺寸、密度等参数,测得该种材料的杨氏模量值。
【实验目的】
①掌握用动态悬挂法测定在室温下金属材料的杨氏模量。
②学习确定试样节点处共振频率的方法(外延法)。
③设计性扩展实验,培养学生综合应用物理仪器及研究探索的科学精神。
【实验原理】
如图4.17.1所示,将一根截面均匀的试样(本实验采用圆截面金属钢棒和铜棒)用两根细金属丝悬挂在两只换能器(一只激振Ⅰ、一只拾振Ⅱ)下面。信号发生器产生一个音频正弦信号通过激振换能器Ⅰ转换成机械振动,由金属悬线传递给试样,激发试样振动,在试样两端自由的条件下试样做横向振动,试样的机械振动再通过另一根悬线传递给换能器Ⅱ,将机械信号还原成电信号,电信号经放大后在示波器上显示出来。
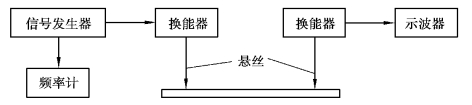
图4.17.1 实验原理
不断调节信号发生器的输出频率,当其频率与试样固有频率一致时,试样共振,通过示波器可以观察到其共振波形振幅突然增加并达到最大。由拾振检测出试样共振时的共振频率f共;再测出试样的几何尺寸、质量等相关参数,根据试样的横振动方程,即可求得材料的杨氏模量E。
如图4.17.2所示,将一均匀棒挂起来,并使之发生横向振动,在一定条件下(l≫d),其横振动方程为

式中,y为竖直方向振动位移;x为横向变量;t为时间;ρ为棒的密度;S为棒的截面面积;E为试样的杨氏模量;J称为其截面的惯性矩(![]() )。可用分离变量法求解该方程(具体求解过程参考本实验参考资料),对圆形棒得
)。可用分离变量法求解该方程(具体求解过程参考本实验参考资料),对圆形棒得
![]()
式中,l为棒长;d为棒直径;m为棒的质量;f为棒横向振动的固有频率,记为f固。在国际单位制中杨氏模量的单位为N·m﹣2。
由式(4.17.1)可知,测定出试样(棒)在不同温度时的固有频率f固及各力学参数,即可计算出它在不同温度时的杨氏模量。测量时可采用如图4.17.2所示的装置。本实验只计算室温下的杨氏模量。
值得指出的是,本实验采用基频振动形式,因为该振动形式相对简单,在推导以上两个公式时也是根据基频的对称性振动导出的,同时需要指出,利用动态悬挂法通过共振求出的频率为共振频率f共,其与试样的固有频率f固有一定的差别,两者关系如下:
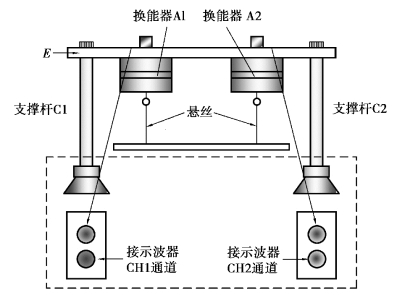
图4.17.2 悬挂式实物

式中,Q为试样的机械品质因数。因为用悬挂法测量杨氏模量时,一般Q值的最小值为50,共振频率和固有频率相比只偏低0.005%,在本实验中测得的是共振频率,由于两者相差极小,故式(4.17.2)中的固有频率f固在数值上可用试样的共振频率f共代替。
实验中有两个问题需加以注意:
①式(4.17.2)给出杨氏模量E的计算公式,其中f是棒横向振动的基频,在实验中要加以判断。
②从图4.17.2中看到测试棒横向振动的激发与拾振是通过悬丝与换能器连接的。若连接点不在棒横向振动的波节上,则横向振动的方程不满足。若连接点就在波节上,则不能激发与拾取试样的振动。因此如何测量f成为实验的关键,一般可采用外延测量法来计算固有频率。具体做法如下:
按照式(4.17.2)的解,测试棒对应基频的横向振动的两个波节分别在0.224l与0.776l处,如图4.17.3所示。
a.先将激振与拾振的两悬丝分别连接在棒0.1l与0.9l上,寻找其共振频率f1。
b.将两悬丝逐渐从每间隔0.02l间距向里推进,分别寻找出对应的频率f2,f3,…,直到悬挂点处于0.22l与0.78l的位置上。
c.以l为横坐标,f为纵坐标作图,将图线延升至0.224l处所对应的f,即为该棒的共振频率f共。
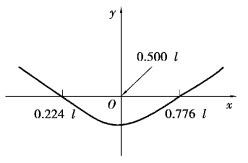
图4.17.3 棒横振动的两个波节
【实验仪器】
电子天平、游标卡尺、信号发生器、悬挂式杨氏模量测试台、示波器等。
【实验内容】
①用游标卡尺分别测量测试棒的各力学量l、d各3次。
②用电子天平分别测量出测试棒的质量m。
③按图4.17.2连接各实验装置,并将悬丝分别连接在测试棒的0.1l与0.9l处。悬挂测试棒细金属丝要保证竖直向下,并保证测试棒与上方仪器横梁平行。
④将两悬丝以每间隔0.02l向里靠拢,分别记下频率f2,f3,…
⑤由小到大逐渐调节信号发生器的频率,并观察示波器信号的变化,通过频率微调,当示波器显示的拾振信号(交流信号)在某一频率处达到极大,则认为信号发生器的激振频率与测试棒共振,并记下该频率f1。
⑥作图计算测试棒的固有频率f。
⑦代入式(4.17.2)计算该棒的杨氏模量。
⑧可换取测试样品重复①~⑥的步骤,求出不同试样的杨氏模量E。数据记录于表4.17.1。
注意:
①关于样品的共振频率f的测量方法,可根据实验现场实际情况,由指导教师指导后测量。
②根据实验原理,要使试样自由振动就应把悬线吊扎在试样的节点上,但这样做就不能激发和拾取试样的振动,因此实际吊扎位置要偏离节点。(https://www.xing528.com)
③仪器频率选择分为三挡:500Hz~1kHz,1~1.5kHz,1.5~2kHz。“频率调节”为频率粗调,“频率微调”为频率的细调,做实验时两者必须配合使用,频率值由5位数码管显示。
【数据处理】
①将测量数据记入表4.17.1。
②正确计算出两种不同材料在室温下杨氏模量值E,通过查阅本书附录,查询室温20℃下相关的杨氏模量值,与之比较求其相对误差,并分析其误差产生的原因。
表4.17.1 数据记录表

【注意事项】
①因换能器为厚度为0.1~0.3mm的压电晶体,用胶粘在0.1mm左右的黄铜片上构成,故极其脆弱,放置测试棒时一定要轻拿轻放,不能用力,也不能敲打。
②两根悬丝必须捆紧,不能松动,且在通过试样轴线的同一截面,测定时应使试样不摆动。
③调节支撑点保证测试棒在竖直方向上振动。
④信号源—换能器(放大器)—示波器均应共“地”。
【思考题】
1.试样的固有频率等于共振频率吗?
2.在实验中根据什么方法判断真假共振峰?
3.还可以用什么方法测定固有频率?
4.动态悬挂法测杨氏模量实验仪的主要工作原理是,首先主机产生_____________(正弦波、方波)电信号,通过换能器1转换为_____________(机械波、电磁波),在被测金属棒中以____________(纵波、横波)的形式传播,然后通过换能器2转换成____________(机械、电)信号输入示波器中。
5.动态悬挂法测杨氏模量实验中,当信号发生器的频率等于试样的____________时,示波器的波形幅度____________,读出的频率就是试样在该温度下的____________。
【参考资料】
用分离变量法求解横振动方程
横振动方程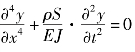 ,用分离变量法求解过程如下:
,用分离变量法求解过程如下:
令y(x,t)=X(x)T(t),代入横振动方程,得
![]()
等式两边分别是x和t的函数,这只有等于一个常数才有可能,该常数设为K4,得
![]()
这两个线性常微分方程的通解分别为
X(x)=B1chKx+B2shKx+B3cosKx+B4sinKx
T(t)=Acos(ωt+φ)
于是解振动方程式的通解为
y(x,t)=(B1chKx+B2shKx+B3cosKx+B4sinKx)Acos(ωt+φ)
其中,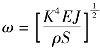 称为频率公式。对任意形状的截面,不同边界条件的试样都是成立的。只要用特定的边界条件定出常数K,并将其代入特定截面的转动惯量J,就可以得到具体条件下的计算公式了。
称为频率公式。对任意形状的截面,不同边界条件的试样都是成立的。只要用特定的边界条件定出常数K,并将其代入特定截面的转动惯量J,就可以得到具体条件下的计算公式了。
如果悬线挂在试样的节点附近,则其边界条件为自用端横向作用力,即
![]()
弯矩为
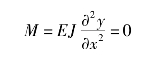
即
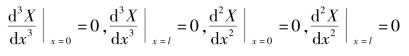
将通解代入边界条件,得到cosKl·chKl=1;用数值解法求得本征值K和棒长应满足
Kl=0,4.730,7.853,10.966,…
由于其中一个根“0”对应静态情况,故将第二个根作为第一个根,记作K1l。一般将K1l所对应的频率称为基频频率。在上述Kml值中,第1,3,5,…个数值对应着“对称形振动”,第2,4,6,…个数值对应着“反对称形振动”。可见试样在作基频振动时,存在两个节点,它们的位置距离断面分别为0.224l和0.776l。将本征值![]() 代入
代入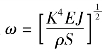 ,得到自由振动的固有频率(基频),即
,得到自由振动的固有频率(基频),即
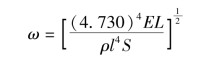
解出杨氏模量为
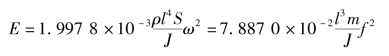
对于圆棒
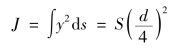
式中,d为圆棒的直径。
得到
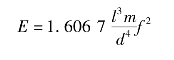
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




